Содержание
- 2. Скалярное произведение векторов a · b = |a| · |b| cos α a · b =
- 3. Косое произведение векторов [a, b] = |a||b|sinθ [a, b] = x1y2 — x2y1.
- 4. По введенным трем числам a, b, c определить существует ли треугольник с такими сторонами. Неравенство треугольника
- 5. Определить существует ли треугольник с такими координатами вершин. Треугольника не существует когда данные три точки лежат
- 6. Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный. Теорема косинусов: Вычислять косинус угла
- 7. По данным сторонам треугольника найти его площадь.
- 8. Вычислить площадь треугольника заданного координатами своих вершин. Косое произведение двух векторов определяет ориентированную площадь параллелограмма основанного
- 9. Вычисление площади многоугольника заданного координатами своих вершин. Метод трапеций S = SA1 A2 B2 B1 +
- 10. Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой. Косое произведение двух
- 11. Симметрия (Время: 1 сек. Память: 16 Мб Сложность: 19%) Многие из вас, вероятно, знакомы с понятием
- 13. var x1,y1,x2,y2,ax,ay,bx,by:longint; begin assign(input,'input.txt'); reset(input); assign(output,'output.txt'); rewrite(output); readln(x1,y1,x2,y2,ax,ay); if x1=x2 then begin bx:=2*x1-ax; by:=ay; end; if
- 14. Треугольник и точка (Время: 1 сек. Память: 16 Мб Сложность: 32%) В декартовой системе координат на
- 17. Фонарики (Время: 1 сек. Память: 16 Мб Сложность: 31%) «Одна голова хорошо, а две лучше. Одна
- 20. Скачать презентацию

![Косое произведение векторов [a, b] = |a||b|sinθ [a, b] = x1y2 — x2y1.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/853513/slide-2.jpg)















 Введение в геометрию
Введение в геометрию Пропорции в нашем мире
Пропорции в нашем мире Как построить треугольник с помощью циркуля
Как построить треугольник с помощью циркуля Закрепление. Повтори правила стр. 72, 74
Закрепление. Повтори правила стр. 72, 74 Считаем в уме
Считаем в уме Простейшие функции и их графики
Простейшие функции и их графики Сочетательное свойство умножения
Сочетательное свойство умножения Геометрический смысл производной
Геометрический смысл производной Презентация на тему Вневписанная окружность
Презентация на тему Вневписанная окружность  Методы решения логарифмических уравнений. 11 класс
Методы решения логарифмических уравнений. 11 класс Определение функций. Построение и чтение графиков функций
Определение функций. Построение и чтение графиков функций Уравнения и неравенства в целых числах
Уравнения и неравенства в целых числах Наибольшее и наименьшее значение функций
Наибольшее и наименьшее значение функций Презентация на тему Расстояние от точки до прямой
Презентация на тему Расстояние от точки до прямой  Единицы площади
Единицы площади Исчисление высказываний
Исчисление высказываний Метрология, стандартизация и сертификация. Статистические критерии
Метрология, стандартизация и сертификация. Статистические критерии Разделительное свойство умножения
Разделительное свойство умножения Квадратные корни. 8 класс
Квадратные корни. 8 класс Определение производной. Её геометрический и физический смысл
Определение производной. Её геометрический и физический смысл Контрольная работа А-7
Контрольная работа А-7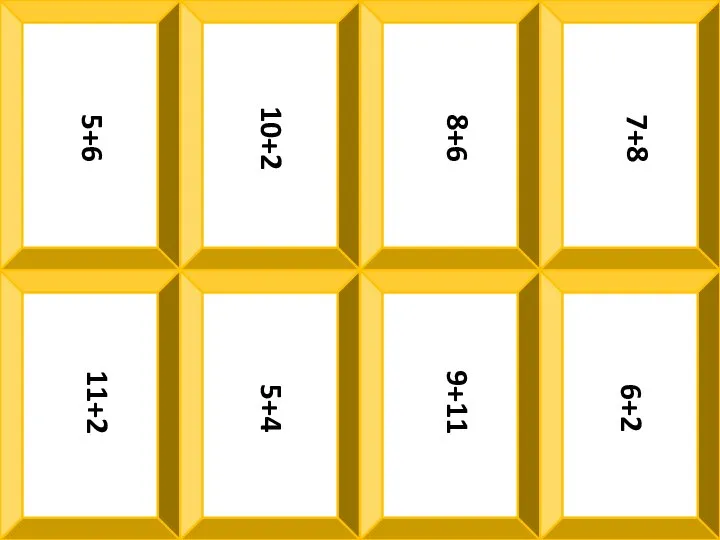 Сумма
Сумма Виды моделирования
Виды моделирования Логика высказываний и булевы алгебры (Boolean Algebra and Logic)
Логика высказываний и булевы алгебры (Boolean Algebra and Logic)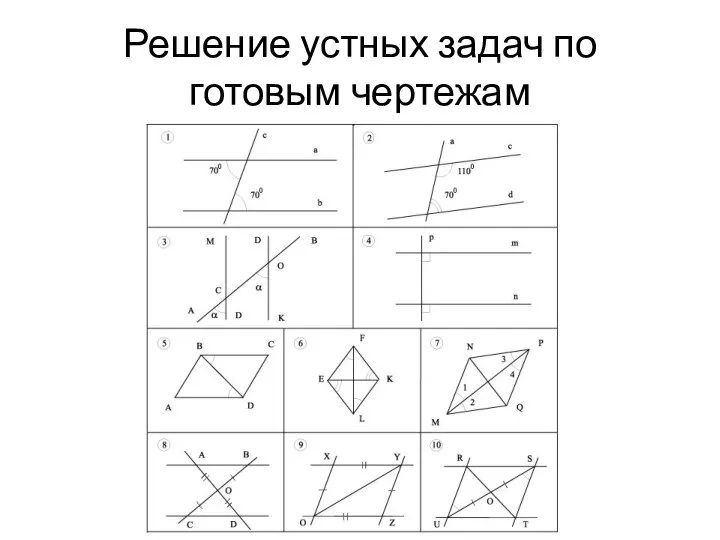 Решение устных задач по готовым чертежам
Решение устных задач по готовым чертежам Презентация на тему Простые числа
Презентация на тему Простые числа  Письмо цифры 6
Письмо цифры 6 тригонометрические неравенства (1)
тригонометрические неравенства (1)