Содержание
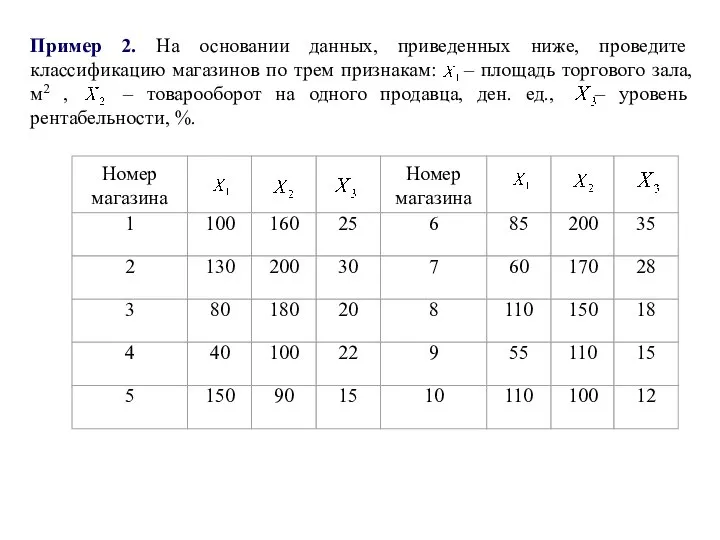
- 2. Пример 2. На основании данных, приведенных ниже, проведите классификацию магазинов по трем признакам: – площадь торгового
- 3. Решение. 1. Рассчитаем расстояния между объектами по евклидовой метрике , где , – стандартизированные значения исходных
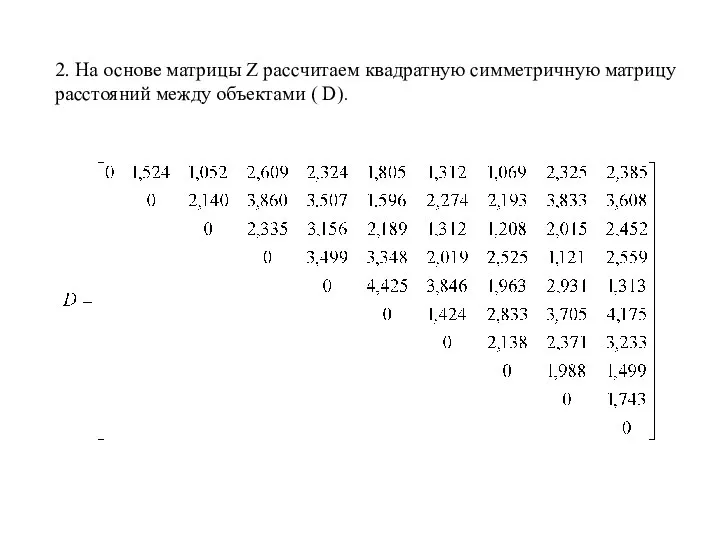
- 4. 2. На основе матрицы Z рассчитаем квадратную симметричную матрицу расстояний между объектами ( D).
- 5. 3. Зададим радиус сферы . В этом случае в сферу попадают объекты, расстояние которых до первого
- 6. 5. Чтобы начать формирование второго кластера, нужно поместить центр сферы в одну из точек, не вошедших
- 7. На основании матрицы Z по евклидовой метрике определяем новые координаты центра для этих точек . Для
- 9. Скачать презентацию




 История теоремы Пифагора
История теоремы Пифагора Презентация на тему Отношения (6 класс)
Презентация на тему Отношения (6 класс)  Волшебная страна - Геометрия
Волшебная страна - Геометрия Решение уравнений
Решение уравнений Порядок элемента. Теорема Лагранжа
Порядок элемента. Теорема Лагранжа Умножение натуральных чисел
Умножение натуральных чисел Объем наклонной призмы
Объем наклонной призмы Задачи на умножение. 2 класс
Задачи на умножение. 2 класс Своя игра. Урок для 6 класса по теме Сложение и вычитание дробей с разными знаменателями
Своя игра. Урок для 6 класса по теме Сложение и вычитание дробей с разными знаменателями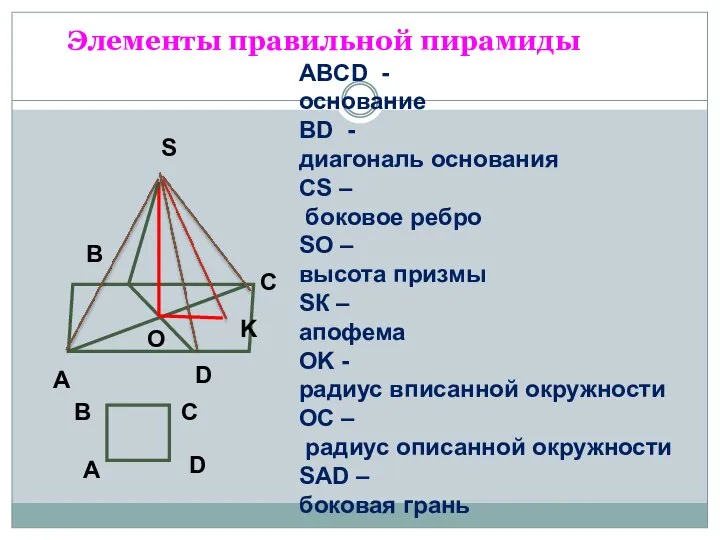 Правильная пирамида
Правильная пирамида Ромб. Свойства ромба
Ромб. Свойства ромба Таблицы данных. Таблицы данных с одной переменной
Таблицы данных. Таблицы данных с одной переменной Геометрические фигуры. 5 класс
Геометрические фигуры. 5 класс Презентация на тему Решение задач с помощью пропорции
Презентация на тему Решение задач с помощью пропорции  Задача №17
Задача №17 Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Усеченный цилиндр
Усеченный цилиндр Состав числа 7
Состав числа 7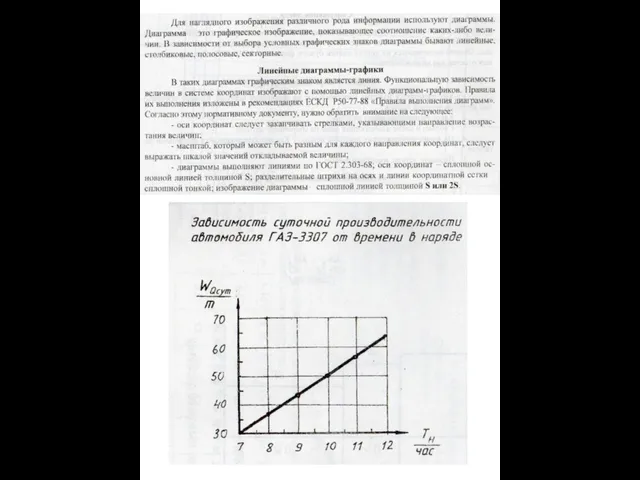 Графики и диаграммы
Графики и диаграммы Интерактивные тренинги по геометрии для подготовки к ОГЭ
Интерактивные тренинги по геометрии для подготовки к ОГЭ Презентация на тему Площадь. Единицы площади
Презентация на тему Площадь. Единицы площади  Что узнали? Чему научились?
Что узнали? Чему научились? Төзек күпкырлыклар
Төзек күпкырлыклар Разложение многочлена на множители
Разложение многочлена на множители Углы треугольника
Углы треугольника Решение задач с пропорциональными величинами
Решение задач с пропорциональными величинами Координати вектора. Модуль вектора
Координати вектора. Модуль вектора Способы решения квадратных уравнений
Способы решения квадратных уравнений