Содержание
- 2. Взвешенный граф Если каждому ребру в графе / дуге в орграфе сопоставлено некоторое число, называемое весом
- 3. Подграф Граф, все вершины и ребра которого принадлежат исходному графу.
- 4. Остовной подграф Остовным называется подграф, которое содержит все вершины исходного графа.
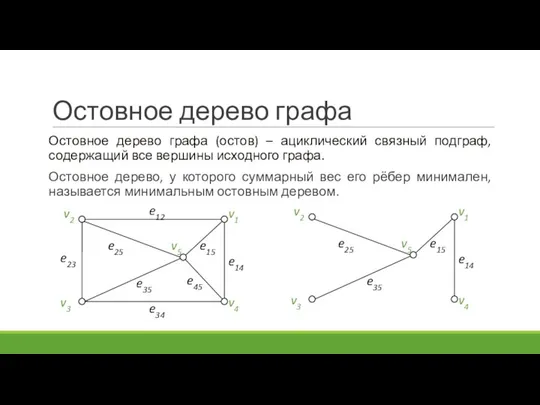
- 5. Остовное дерево графа Остовное дерево графа (остов) – ациклический связный подграф, содержащий все вершины исходного графа.
- 6. Теорема Кирхгофа
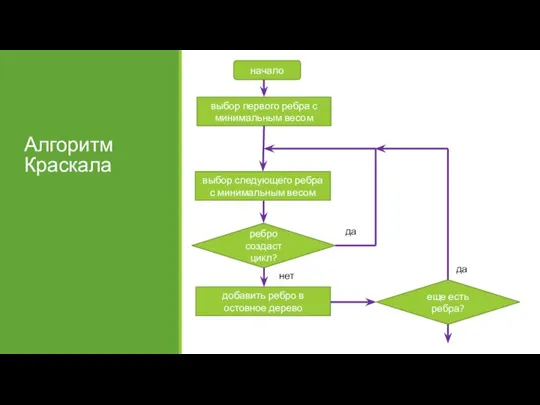
- 7. Алгоритм Краскала, 1956 Сортируем ребра графа по возрастанию весов. Полагаем, что каждая вершина относится к своей
- 8. Алгоритм Краскала
- 9. Алгоритм Прима На каждом шаге вычеркиваем из графа дугу максимальной стоимости с тем условием, что она
- 10. Задача Телевизионная компания планирует подключение к своей кабельной сети пяти новых районов. На рисунке показана структура
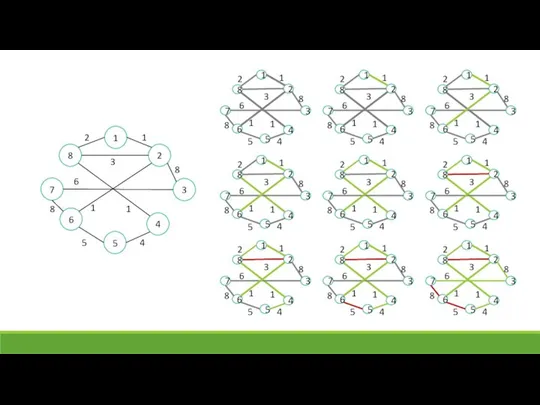
- 11. Ребра AD и CE имеют минимальный вес, равный 5. Произвольно выбирается ребро AD (выделено на рисунке).
- 12. Следующие ребра — AB и BE с весом 7. Произвольно выбирается ребро AB, выделенное на рисунке.
- 14. Поиск минимального пути
- 15. Алгоритм Флойда-Уоршелла
- 16. Алгоритм Флойда-Уоршелла
- 17. Восстановление пути в алгоритме Флойда-Уоршелла
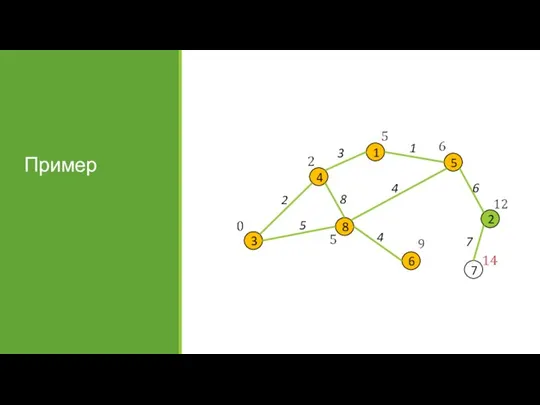
- 18. Пример Матрица смежности:
- 19. Пример Матрица 1-расстояний
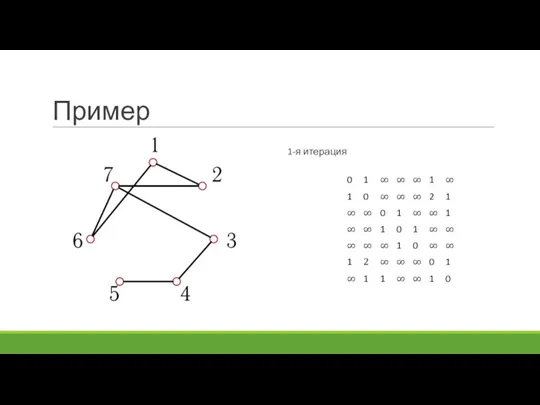
- 20. Пример 1-я итерация
- 21. Пример 2-я итерация
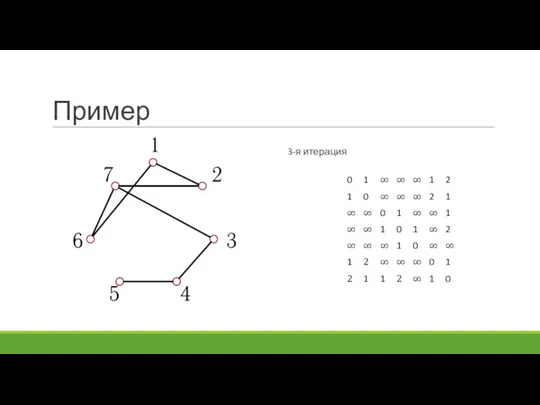
- 22. Пример 3-я итерация
- 23. Пример 4, 5, 6 итерации
- 24. Пример Матрица кратчайших расстояний:
- 25. Алгоритм Дейкстры
- 26. Алгоритм Дейкстры
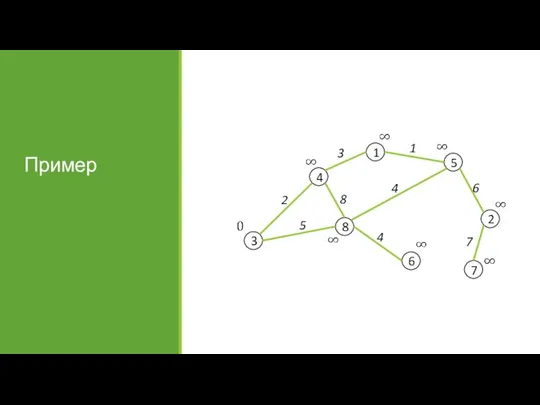
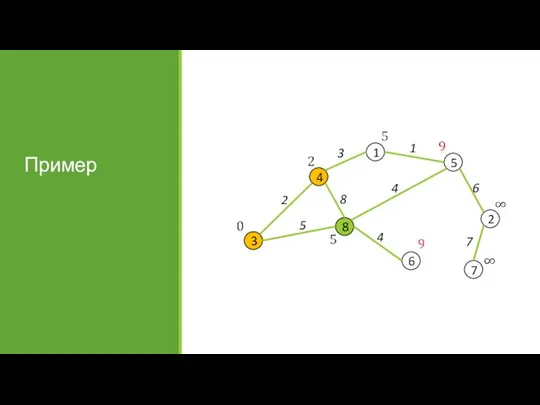
- 27. Пример
- 28. Пример
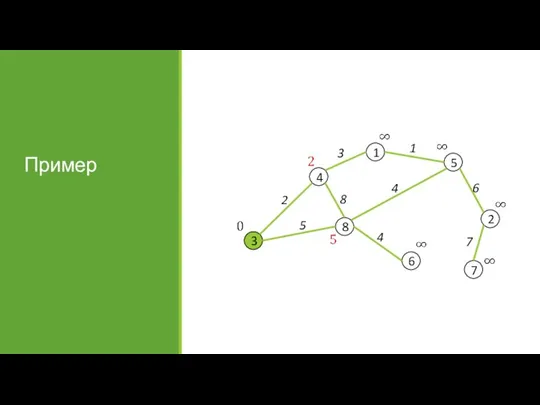
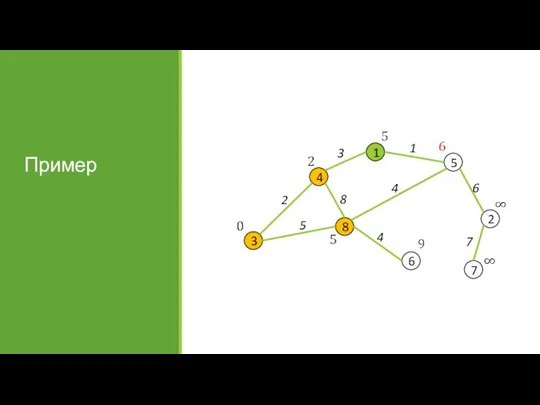
- 29. Пример
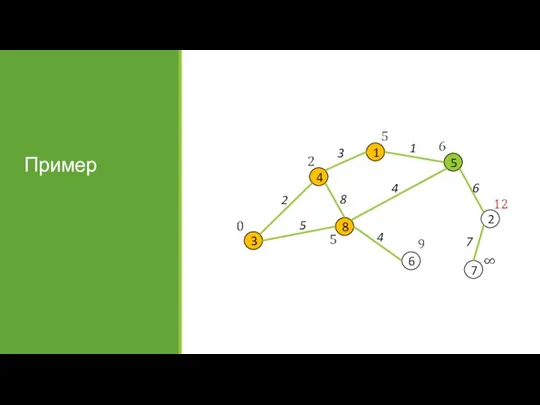
- 30. Пример
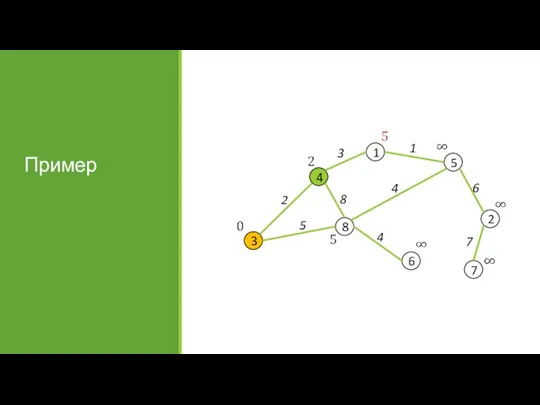
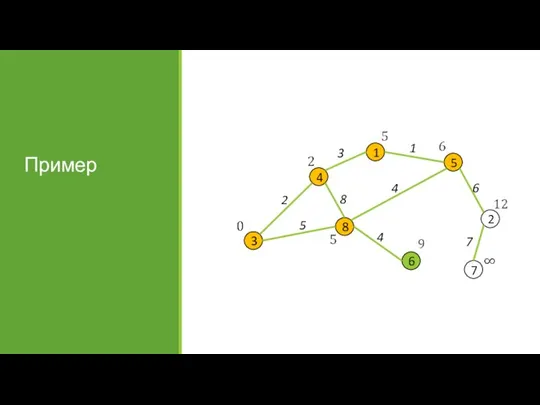
- 31. Пример
- 32. Пример
- 33. Пример
- 34. Пример
- 36. Скачать презентацию




















 Равносильность формул логики. Законы логики
Равносильность формул логики. Законы логики Теорема Пифагора. Задачи на чертежах
Теорема Пифагора. Задачи на чертежах Двугранный угол. Линейный угол
Двугранный угол. Линейный угол Презентация_по_алгебре_Возрастание_и_убывание_фу
Презентация_по_алгебре_Возрастание_и_убывание_фу Урок-КВН
Урок-КВН Элементы комбинаторики
Элементы комбинаторики Умножение. Законы умножения
Умножение. Законы умножения Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Числовые и буквенные выражения. (5 класс)
Числовые и буквенные выражения. (5 класс) Действия с рациональными числами
Действия с рациональными числами Исходные понятия теории множеств
Исходные понятия теории множеств Занимательные задачи
Занимательные задачи Бесконечные периодические десятичные дроби
Бесконечные периодические десятичные дроби Анализ задач и альтернативные методы решений. Мастер-класс
Анализ задач и альтернативные методы решений. Мастер-класс Математика-2
Математика-2 Решение задач на применение свойств прямоугольных треугольников
Решение задач на применение свойств прямоугольных треугольников матем урок 4-5
матем урок 4-5 Теория вероятностей. Лекция 4
Теория вероятностей. Лекция 4 Математическая статистика результатов ЕГЭ
Математическая статистика результатов ЕГЭ Признаки равенства треугольников
Признаки равенства треугольников Алгоритм Евклида
Алгоритм Евклида Математика вокруг нас. Геометрический облик бульвара имени академика Кикоина
Математика вокруг нас. Геометрический облик бульвара имени академика Кикоина Рівняння дотичної до графіка функції
Рівняння дотичної до графіка функції Уравнение с двумя переменными и его график
Уравнение с двумя переменными и его график Дорогу осилит идущий, а математику мыслящий
Дорогу осилит идущий, а математику мыслящий Занимательная математика
Занимательная математика Презентация на тему Повторение курса начальной школы в 5-м классе
Презентация на тему Повторение курса начальной школы в 5-м классе  Развертка. Создание объёмных фигур из плоскости
Развертка. Создание объёмных фигур из плоскости