Слайд 2Основные понятия комбинаторики.
Основными понятиями комбинаторики являются:
правило суммы,
правило произведения,
расстановки,
перестановки,

размещение,
сочетание.
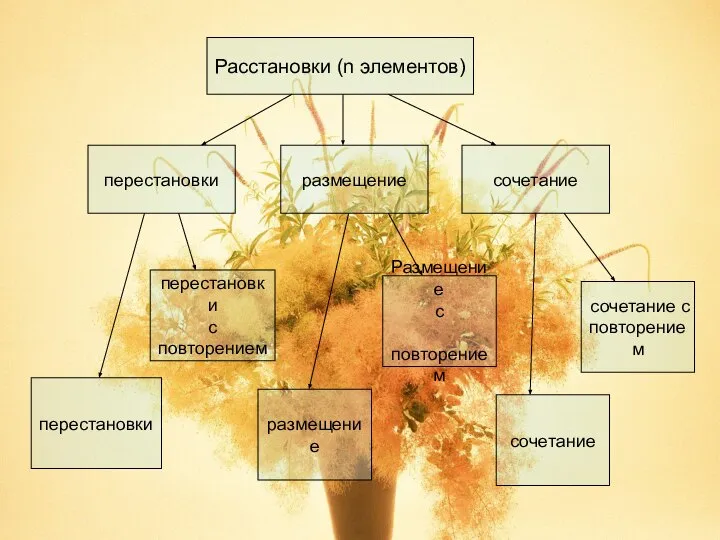
Слайд 3Расстановки (n элементов)
перестановки
размещение
сочетание
перестановки
перестановки
с повторением
размещение
Размещение
с
повторением
сочетание
сочетание с
повторением
Слайд 4Опр.: Область математики, в которой изучаются вопросы о том, сколько различных комбинаций

можно составить из заданных объектов, называется комбинаторикой.
Слайд 5Задачи комбинаторики очень тесно связаны с задачами линейного программирования.
Пример: сколько можно составить

трехзначных номеров, не содержащих нуля?
Решение: составляю девять однозначных номеров: 1,2,..,9. Если взять набор из 10 цифр, написать любую из 9 кроме 0, то из каждого однозначного получится 9 двузначных: 9*9=81 двухместный номер. Тогда 81*9=729 трехзначных номеров без повторения.
Слайд 6Размещение с повторением
Опр.: Пусть имеется множество из n-элементов. Из него выбираем подмножества,

состоящие из k-элементов. При этом подмножества могут отличаться как самими элементами, так и порядком расположения элементов относительно друг друга. Назовем выбор таких подмножеств k-размещением с повторениями. Обозначение:
Слайд 7Пример: для запирания сейфов в автоматических замках набирается секретное слово. Пусть имеется

12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток можно совершить, не зная кода?
Решение: . следовательно, неудачных попыток можно совершить 248831.
Слайд 8Общие правила комбинаторики
Большинство задач комбинаторики сводятся к решению с помощью правила суммы

и правила произведения.
Правило суммы. Часто все известные комбинации разбиваются на классы, причем каждая комбинация входит только в один класс. В этом случае общее число комбинаций равно сумме чисел комбинаций во всех классах.
Слайд 9Пример: если некоторый объект А:m-способами, а В:n-способами, то выбор либо А, либо

В можно совершить m+n-способами. При этом важно, чтобы комбинации не совпадали. Если такие совпадения есть, то m+n-k – число выбора, где k- количество совпадений.
Слайд 10Часто при составлении комбинаций из этих элементов известно, сколькими способами можно выбрать

первый элемент, и сколькими второй. При этом число выбора второго элемента не зависит от числа выбора первого.
Правило произведения: Пусть первый элемент выбирается n способами, второй – m способами. Тогда пару можно выбрать m*n способами.
Слайд 11Обобщение: Если выбираются не пары элементов, а комбинации из общего числа элементов,

то приходим к задаче вида: сколько можно составить k-множеств, если
1-й элемент € n1;
2-й € n2;
…
n-й € nk.
При этом две расстановки считаются различными, если хотя бы на одном месте стоят различные элементы. В этой ситуации имеем n1*n2*...*nk вариантов.
Слайд 12Сложнее решаются задачи, в которых число выбора каждого последующего шага зависит от

выбор на предыдущем шаге.
Пример: сколькими способами из 28 костей домино можно выбрать 2 кости, чтобы их можно было приложить друг к другу?
Решение. Это можно сделать 28 способами, при этом 7 случаев выбора дубля, остальные 21 – различные числа. В первом случае 6 способов выбора второй кости, во втором – 12. По правилу произведения имеем 7*6=42 варианта выбора в первом случае, а во втором – 21*12=252 варианта. 42+252 = 294 варианта всего. Если не учитывать порядок выбора костей, то имеем 294/2=147 способов выбора.
Слайд 13Размещение без повторения.
Сколько можно составить размещений без повторений, если все входящие элементы

различны?
Имеется множество из n-элементов. Сколько из этих элементов можно составить подмножеств, состоящих из k-элементов? При этом подмножества различаются, если они отличаются хотя бы одним элементом. Получаем количество размещений: . На первом шаге имеем n-выборов, на втором – n-1, на пятом шаге – n-k+1 выбора. Количество элементов выбора:
Слайд 14Пример. Имеется 25 человек. Из них нужно выбрать старосту, культурга и профорга.

Сколькими способами можно это сделать, если каждый человек занимал лишь одну должность?
Решение: вариантов.
Слайд 15Перестановки без повторения.
Опр.: Перестановки, в которые входят все элементы, но отличаются только

порядком расположения. Такие перестановки называются n-перестановки без повторения.
По определению, 0!=1.
Пример. Сколькими способами можно разместить за столом 10 гостей?
Решение: Р10=10!=3628800 вариантов.
Слайд 16Перестановки с повторениями
Если некоторые переставляемые элементы одинаковы, то некоторые перестановки будут совпадать

друг с другом, и общее количество перестановок получится гораздо меньше, чем предполагалось.
Слайд 17Сочетание.
Числом сочетаний из n по m (n>=k) называется величина
Пример:

Слайд 18Сочетания с повторениями.
Имеются предметы n различных типов. Сколько k-комбинаций можно из них

сделать, если не принимать во внимание порядок комбинаций?
Слайд 19Свойства сочетаний.
1.
Пример:
Доказательство:
2.
Доказательство:

Слайд 203.
Доказывается методом математической индукции.
4.
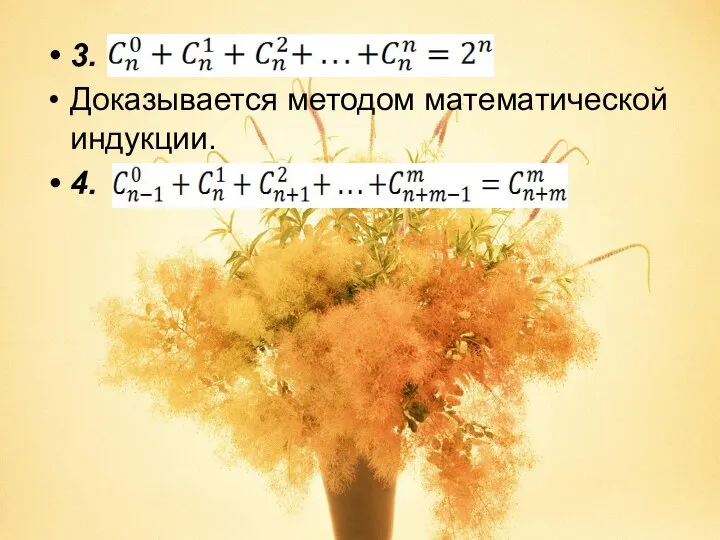


















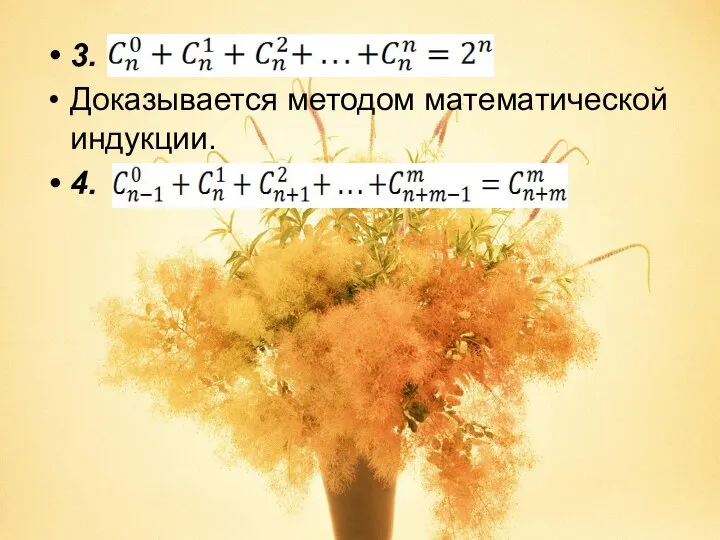
 Промежуточная аттестация по геометрии
Промежуточная аттестация по геометрии Правильные многоугольники
Правильные многоугольники Алгоритмы и способы их описания
Алгоритмы и способы их описания Число или цифра 5
Число или цифра 5 Разработка программы для нахождения корней уравнения методом половинного деления или другим методом
Разработка программы для нахождения корней уравнения методом половинного деления или другим методом Четырехугольники
Четырехугольники Преобразования систем координат
Преобразования систем координат Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление
Урок №52. Присчитывание и отсчитывание по 3. Состав чисел. Закрепление Формулы сложения
Формулы сложения Теорема Фалеса. (8 класс)
Теорема Фалеса. (8 класс) Сочетания. В чем отличие от размещений?
Сочетания. В чем отличие от размещений? Решение логических задач
Решение логических задач Разложение многочлена на множители с помощью формулы сокращенного умножения
Разложение многочлена на множители с помощью формулы сокращенного умножения Порядок действий в выражениях без скобок и со скобками
Порядок действий в выражениях без скобок и со скобками Классическое определение вероятности
Классическое определение вероятности Математические ребусы. 6 класс
Математические ребусы. 6 класс Сумма углов треугольника
Сумма углов треугольника Площадь поверхности призмы
Площадь поверхности призмы Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Формула суммы n первых членов геометрической прогрессии
Формула суммы n первых членов геометрической прогрессии Пространство
Пространство Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой Где логика. Игра
Где логика. Игра Лекция 2. Средние величины
Лекция 2. Средние величины Аттестационная работа. Сослужит ли добрую службу математика экологии
Аттестационная работа. Сослужит ли добрую службу математика экологии Можно ли без шаблона разметить круг?
Можно ли без шаблона разметить круг? Задания Кириллу
Задания Кириллу Угол
Угол