Содержание
- 2. Теория автоматов — раздел дискретной математики, изучающий абстрактные автоматы — вычислительные машины, представленные в виде математических
- 3. Символ — любой атомарный блок данных, который может производить эффект на машину. Чаще всего символ —
- 4. Автоматы могут быть: Детерминированные Недетерминированные
- 5. Детерминированный конечный автомат (ДКА) — последовательность (кортеж) из пяти элементов (Q , Σ , δ ,
- 6. Недетерминированный конечный автомат (НКА) — последовательность (кортеж) из пяти элементов (Q , Σ , ∆, S,
- 7. СЛОВО Автомат читает конечную строку символов a1,a2,…., an , где ai ∈ Σ, которая называется входным
- 8. ПРИНИМАЕМОЕ СЛОВО
- 9. ПРИМЕНЕНИЕ Теория автоматов лежит в основе всех цифровых технологий и программного обеспечения, так например компьютер является
- 11. Скачать презентацию








 Решение задач. Диагностика 1
Решение задач. Диагностика 1 Математический диктант. 6 класс
Математический диктант. 6 класс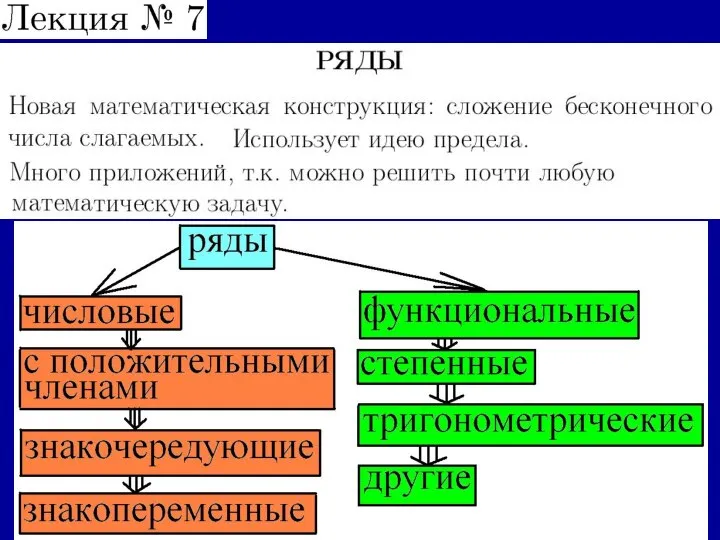 Числовые ряды
Числовые ряды Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма
Обзор мультимедийных дисков по математике 1. Виртуальная школа Кирилла и Мефодия. 2. Серия «Все задачи школьной математики». 3. «Ма Повторим правила образования и записи чисел
Повторим правила образования и записи чисел Диофантово уравнение
Диофантово уравнение Векторы
Векторы Задачі_на_наслідки_із_аксіом_стереометрії
Задачі_на_наслідки_із_аксіом_стереометрії Числовые головоломки
Числовые головоломки 6cc84cfba09801fa77f2178065bede8f
6cc84cfba09801fa77f2178065bede8f Методы оптимизации. Ограничения в виде равенств и неравенств
Методы оптимизации. Ограничения в виде равенств и неравенств Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК)
Наибольший общий делитель (НОД) и наименьшее общее кратное чисел (НОК) Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка
Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка Regresní a korelační analýza
Regresní a korelační analýza Предел функции (часть 2)
Предел функции (часть 2)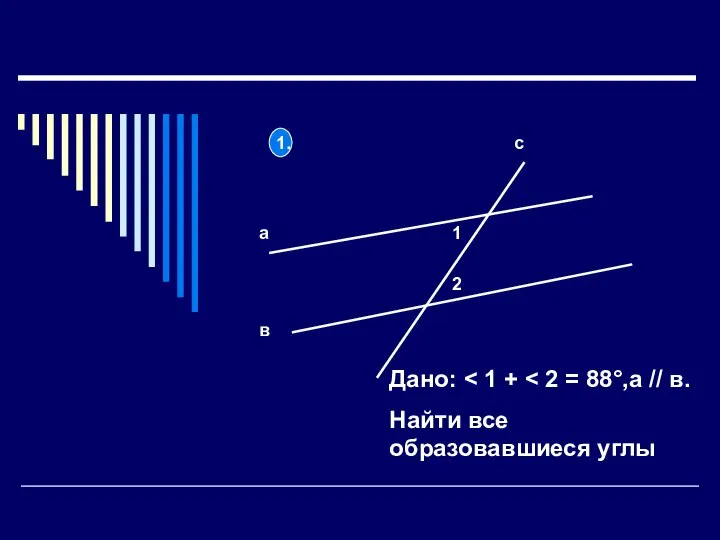 Признаки равенства треугольников
Признаки равенства треугольников Угол между прямой и плоскостью. Теорема о трёх перпендикулярах
Угол между прямой и плоскостью. Теорема о трёх перпендикулярах Подготовка к ЕГЭ (профильный уровень). Задания 5
Подготовка к ЕГЭ (профильный уровень). Задания 5 Уравнения и неравенства в целых числах
Уравнения и неравенства в целых числах Теорема Виета. Устная работа
Теорема Виета. Устная работа Минимизация переключательных функций
Минимизация переключательных функций Прямая и плоскость в пространстве. Лекция 6
Прямая и плоскость в пространстве. Лекция 6 Таблица умножения девяти. Тренажёр-раскраска
Таблица умножения девяти. Тренажёр-раскраска Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая
Методика изучения одномерных геометрических фигур в курсе математики начальных классов: точка, линия, прямая Диаграммы Ламерея. Качественный анализ дискретных ДС
Диаграммы Ламерея. Качественный анализ дискретных ДС Сложение десятичных дробей
Сложение десятичных дробей