- Главная
- Математика
- Задача № 5 з математики. Команда “Леонардо”

Содержание
Слайд 2Умова задачі
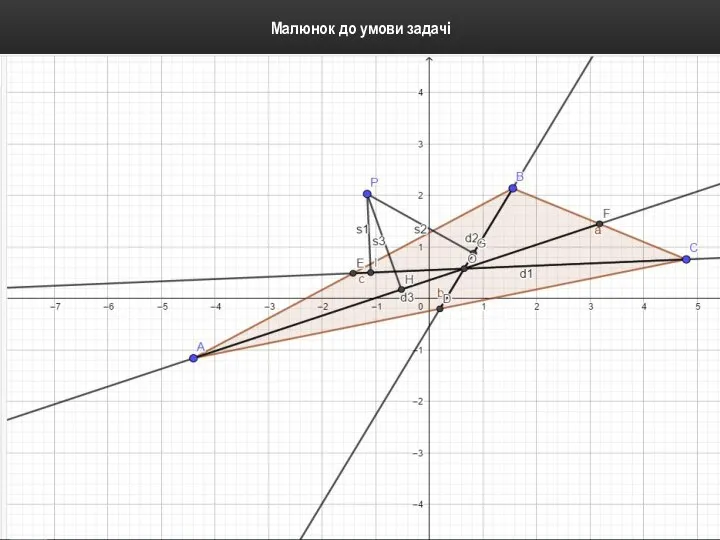
d1, d2, d3 – довжини медіан трикутника, P – довільна точка
Умова задачі
d1, d2, d3 – довжини медіан трикутника, P – довільна точка

площини, а s1, s2, s3 – відстані від точки Р до прямих, які містять відповідні медіани. Доведіть, що один із трьох добутків d1s1, d2s2, d3s3 дорівнює сумі двох інших.
Слайд 3Малюнок до умови задачі
Малюнок до умови задачі
Слайд 4Розв’язання
1. Виберемо один із кутів на які ділять площину три медіани та
Розв’язання
1. Виберемо один із кутів на які ділять площину три медіани та

який містить в собі т. Р
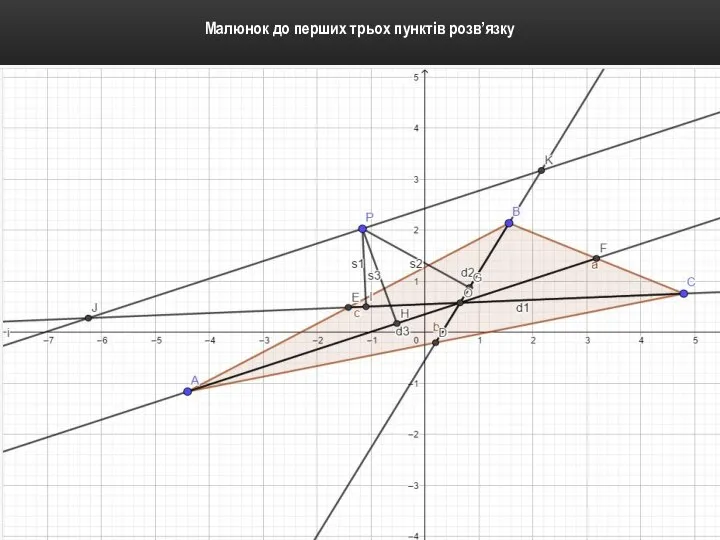
2. Проведемо через т. Р пряму, яка у нашому випадку паралельна d3.
3. Утвориться трикутник OJK.
2. Проведемо через т. Р пряму, яка у нашому випадку паралельна d3.
3. Утвориться трикутник OJK.
Слайд 5Малюнок до перших трьох пунктів розв’язку
Малюнок до перших трьох пунктів розв’язку
- Предыдущая
Работа в https://learningapps.orgСледующая -
Викторина по автоспорту умножение десятичных дробей. Работа в паре
умножение десятичных дробей. Работа в паре Прямоугольный параллелепипед. Многогранники
Прямоугольный параллелепипед. Многогранники Численные методы решения дифференциальных уравнений
Численные методы решения дифференциальных уравнений Исследование функций
Исследование функций Логические законы
Логические законы Десятичные числа
Десятичные числа Направления и лучи
Направления и лучи Алгебра логики
Алгебра логики Таблицы данных. Таблицы данных с одной переменной
Таблицы данных. Таблицы данных с одной переменной Презентация на тему Признаки делимости от 2 до 15
Презентация на тему Признаки делимости от 2 до 15  Вычисление площадей плоских фигур в прямоугольной системе координат (Лекция 3)
Вычисление площадей плоских фигур в прямоугольной системе координат (Лекция 3) Исследование функции на монотонность. Экстремумы функции. Построение графиков функций с применением производной
Исследование функции на монотонность. Экстремумы функции. Построение графиков функций с применением производной История развития обыкновенных дробей
История развития обыкновенных дробей Движение. Виды движения
Движение. Виды движения Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций Веселый математический поезд
Веселый математический поезд Теория вероятностей. Вычисление вероятности выигрыша
Теория вероятностей. Вычисление вероятности выигрыша Приёмы устных вычислений вида: 470 + 80, 560 - 90
Приёмы устных вычислений вида: 470 + 80, 560 - 90 Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№10)
Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№10)  Множество, функция, отображение, операция. Лекция 1
Множество, функция, отображение, операция. Лекция 1 Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи
Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи Презентация на тему Метод координат в пространстве
Презентация на тему Метод координат в пространстве  Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Многогранники
Многогранники Лето в цифрах. Маршрут поездки
Лето в цифрах. Маршрут поездки Функция нескольких переменных. Общие свойства. Непрерывность функции. Линии уровня, поверхности уровня. (Семинар 21)
Функция нескольких переменных. Общие свойства. Непрерывность функции. Линии уровня, поверхности уровня. (Семинар 21) Задачи для всех-всех-всех
Задачи для всех-всех-всех Методика изучения площади. История развития понятия площади
Методика изучения площади. История развития понятия площади