Содержание
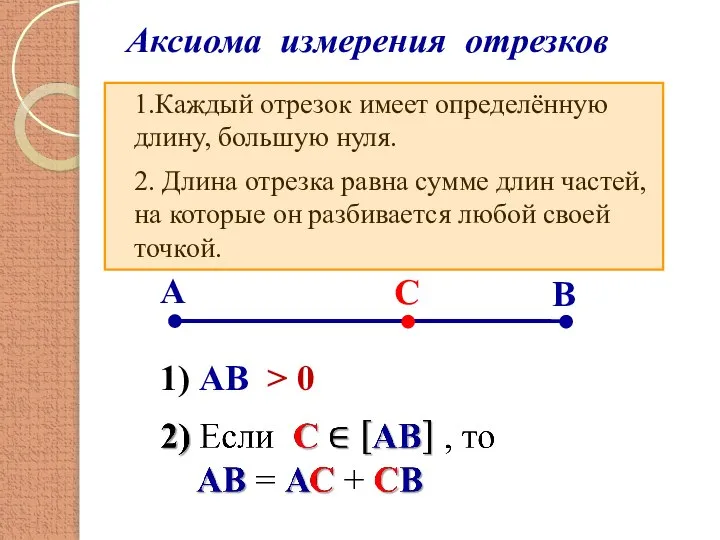
- 2. Аксиома измерения отрезков 1.Каждый отрезок имеет определённую длину, большую нуля. 2. Длина отрезка равна сумме длин
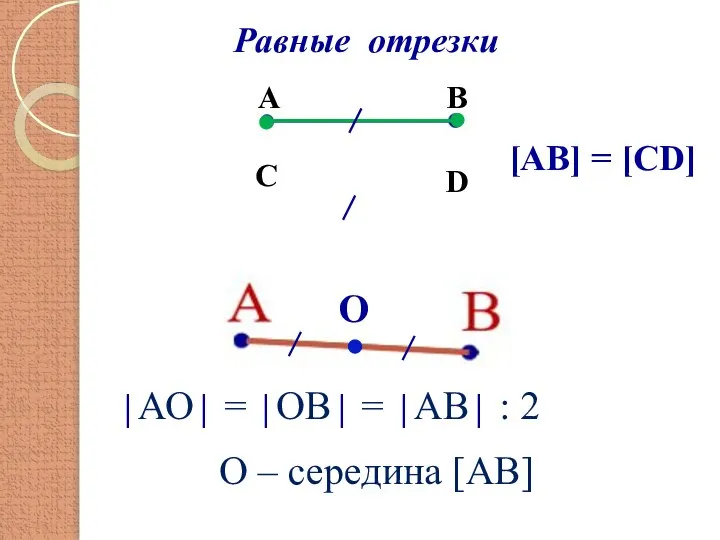
- 3. Равные отрезки О │АО│ = │ОВ│ = │АВ│ : 2 О – середина [АВ] А В
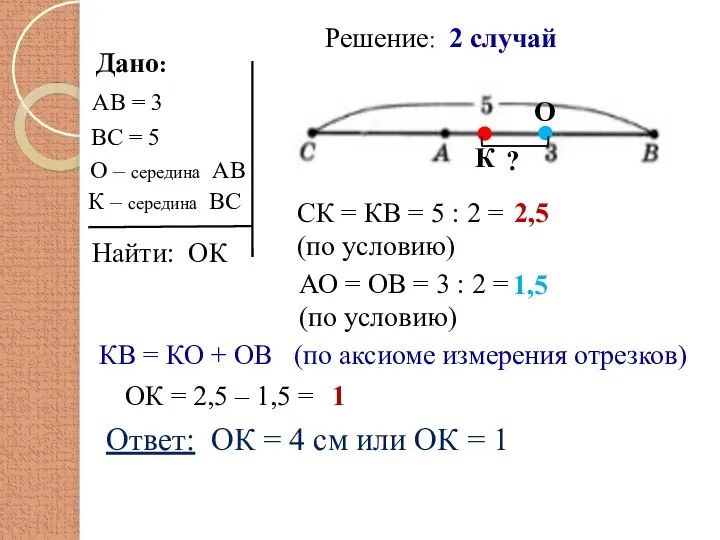
- 4. Дано: Найти: ОК Решение: 1 случай АО = ОВ = 3 : 2 = (по условию)
- 5. Дано: Найти: ОК АО = ОВ = 3 : 2 = (по условию) ОК = 2,5
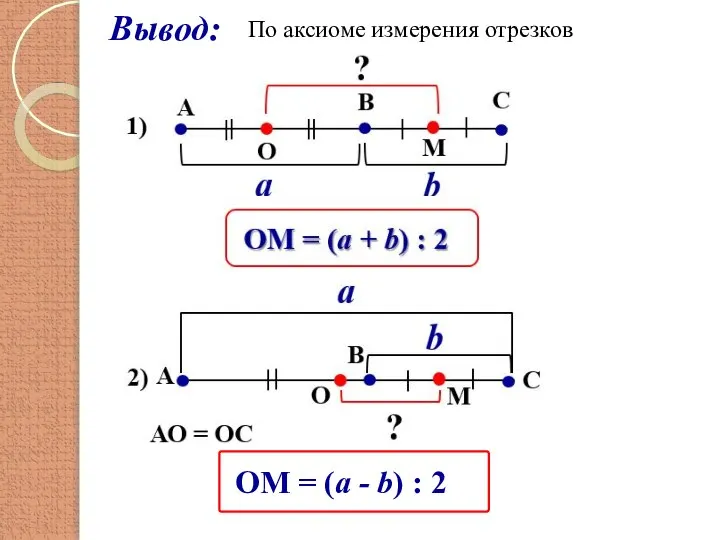
- 6. Вывод: По аксиоме измерения отрезков ОМ = (a - b) : 2
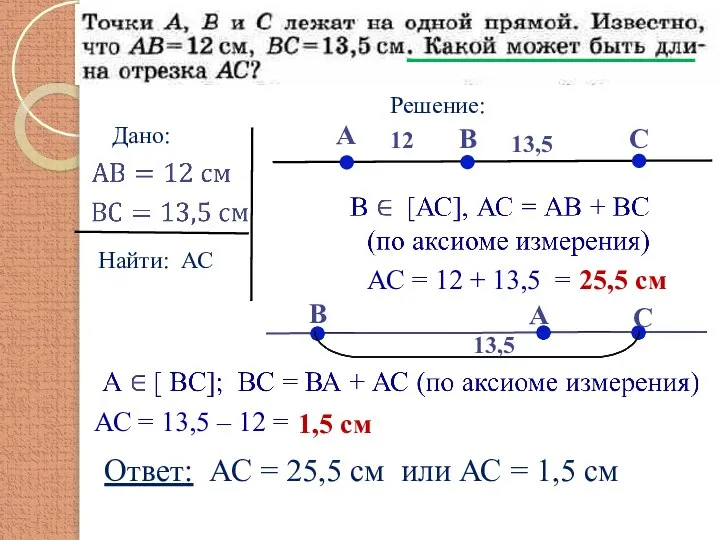
- 7. Дано: Найти: АС А В С 12 13,5 АС = 12 + 13,5 = 25,5 см
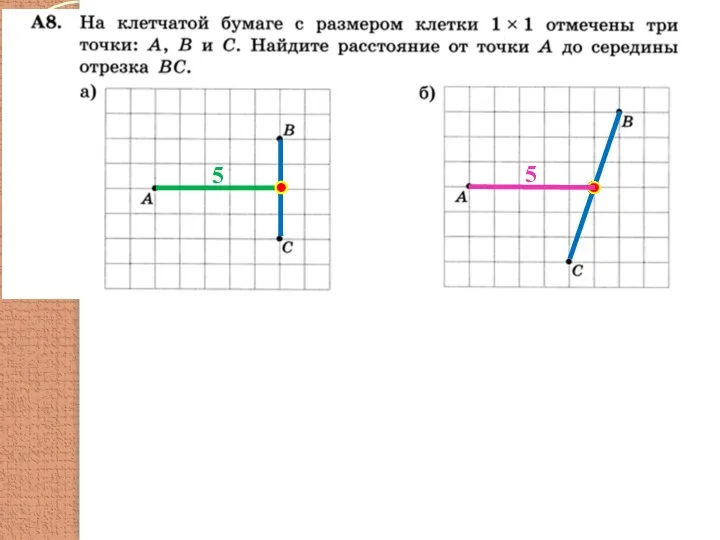
- 8. 5 5
- 9. №1 №14 АМ : МВ = 4 : 3 АВ = 14 МВ = ? АВ
- 15. Скачать презентацию






 Касательная к окружности. Решение задач
Касательная к окружности. Решение задач Конструктор (4)
Конструктор (4) Векторная алгебра
Векторная алгебра Таблица умножения и деления на 2
Таблица умножения и деления на 2 Ментальная арифметика
Ментальная арифметика Медиана треугольника
Медиана треугольника Теория массового обслуживания
Теория массового обслуживания Презентация на тему Уравнения
Презентация на тему Уравнения  Гра в нормальній формі. Формалізований вид гри
Гра в нормальній формі. Формалізований вид гри Понятие многогранника. Геометрические фигуры
Понятие многогранника. Геометрические фигуры Множества и операции над ними
Множества и операции над ними Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач. ГИА 2013. Задачи №23
Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач. ГИА 2013. Задачи №23 Проецирование правильной шестиугольной призмы
Проецирование правильной шестиугольной призмы Единицы счёта
Единицы счёта Презентация на тему Изучаем натуральные числа
Презентация на тему Изучаем натуральные числа  Квадратные уравнения
Квадратные уравнения Презентация на тему Треугольник
Презентация на тему Треугольник  Сечение многогранника плоскостью
Сечение многогранника плоскостью Задачи на движение. Нахождение времени. Взаимосвязь между величинами: скорость, время, расстояни
Задачи на движение. Нахождение времени. Взаимосвязь между величинами: скорость, время, расстояни Формулы. Урок 1
Формулы. Урок 1 Проецирование геометрических тел. Анализ геометрической формы
Проецирование геометрических тел. Анализ геометрической формы Сложение вида 37+48. Урок №71
Сложение вида 37+48. Урок №71 Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Системы неравенств с двумя переменными
Системы неравенств с двумя переменными Математическое моделирование. Тестирование
Математическое моделирование. Тестирование Задачи на построение
Задачи на построение Параллельность прямых и плоскостей (10 класс)
Параллельность прямых и плоскостей (10 класс)