Содержание
- 2. Содержание: Цели и задачи Определение производной Физический смысл производной Правила дифференцирования Основные формулы производных Примеры взятия
- 3. Цели и задачи Знать определение производной; Знать и уметь применять правила дифференцирования; Знать и уметь применять
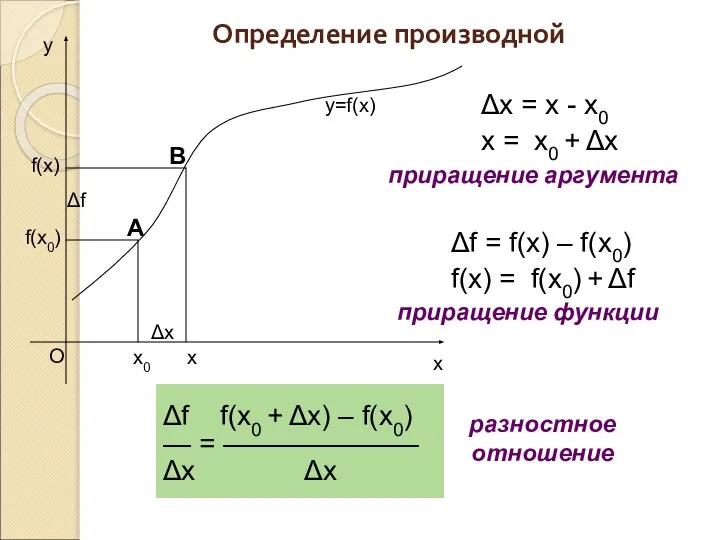
- 4. x0 Δx f(x0) x f(x) Δf y=f(x) Δx = x - x0 x = x0 +
- 5. Производной функции f в точке x0 называется число, к которому стремится разностное отношение при Δx →
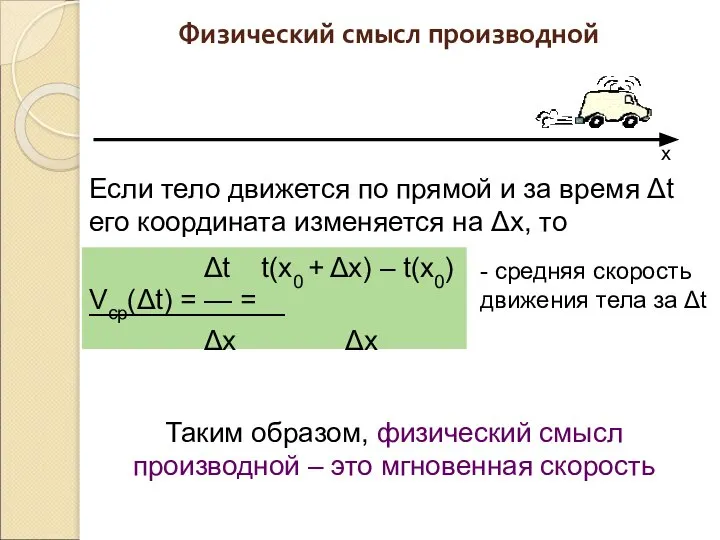
- 6. x Если тело движется по прямой и за время Δt его координата изменяется на Δx, то
- 7. Правила дифференцирования Если функция y = f(x) имеет производную, то она называется дифференцируемой; операция нахождения производной
- 8. Основные формулы производных
- 9. Примеры взятия производной
- 10. Производные элементарных функций
- 11. Производная сложной функции Пусть f(x) , g(x) – дифференцируемые функции. Тогда: Пример:
- 12. Задания для закрепления материала Найдите производные, используя образцы. Образец: Образец:
- 13. Образец: Образец:
- 14. Для каждой из функций, графики которых изображены в верхнем ряду, найдите график ее производной.
- 15. Задания для самоанализа Задание 1. Найдите производные функций:
- 17. Скачать презентацию












 Арифметический квадратный корень. Самостоятельная работа
Арифметический квадратный корень. Самостоятельная работа Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Наибольшее и наименьшее значение функций
Наибольшее и наименьшее значение функций Презентация на тему Готфрид Вильгельм Лейбниц
Презентация на тему Готфрид Вильгельм Лейбниц 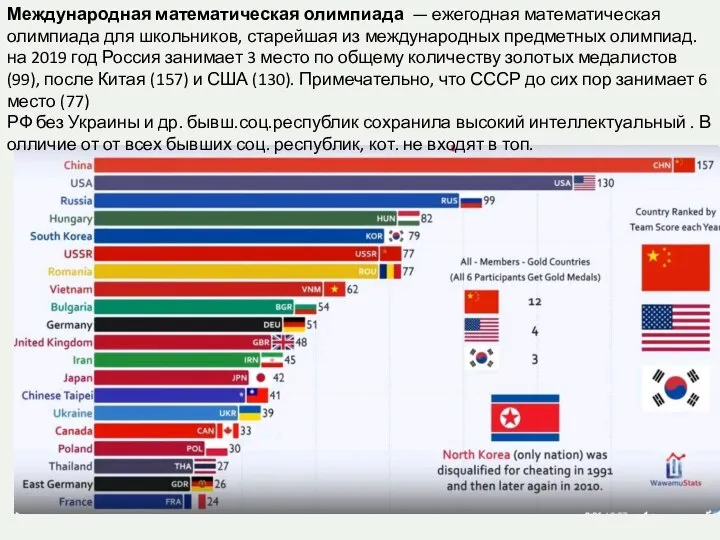 Международная математическая олимпиада
Международная математическая олимпиада Многоугольники в нашей жизни
Многоугольники в нашей жизни Формирование математических представлений, умений и навыков у дошкольников
Формирование математических представлений, умений и навыков у дошкольников Геометрический смысл производной. Производная и её геометрический смысл
Геометрический смысл производной. Производная и её геометрический смысл Согласные звуки [в],[ в’], буквы В, в
Согласные звуки [в],[ в’], буквы В, в Векторы в пространстве
Векторы в пространстве Пример записи решения задания к Части I РГР №1
Пример записи решения задания к Части I РГР №1 Презентация на тему Неопределенный интеграл
Презентация на тему Неопределенный интеграл  Статистический анализ случайных погрешностей
Статистический анализ случайных погрешностей Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Понятие области
Понятие области Проценты. 5 класс
Проценты. 5 класс Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Окружность и круг
Окружность и круг Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Презентация на тему Формулы дифференцирования
Презентация на тему Формулы дифференцирования  Прибавить и вычесть 4
Прибавить и вычесть 4 Проценты. Устная работа
Проценты. Устная работа Реляционная алгебра
Реляционная алгебра Системы неравенств
Системы неравенств Задачи о зиме
Задачи о зиме Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ  Способы задания арифметической прогрессии
Способы задания арифметической прогрессии Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7
Презентация на тему ГИА 2013. Модуль АЛГЕБРА №7