Экспертная система поддержки принятия решений в оценке риска генетического бесплодия и спонтанного прерывания беременности

Задача классифика́ции
формализованная задача, в которой имеется множество объектов (ситуаций), разделённых некоторым образом на классы. Задано конечное множество объектов, для которых известно, к каким классам они относятся. Это множество называется выборкой. Классовая принадлежность остальных объектов неизвестна. Требуется построить алгоритм, способный классифицировать произвольный объект из исходного множества.

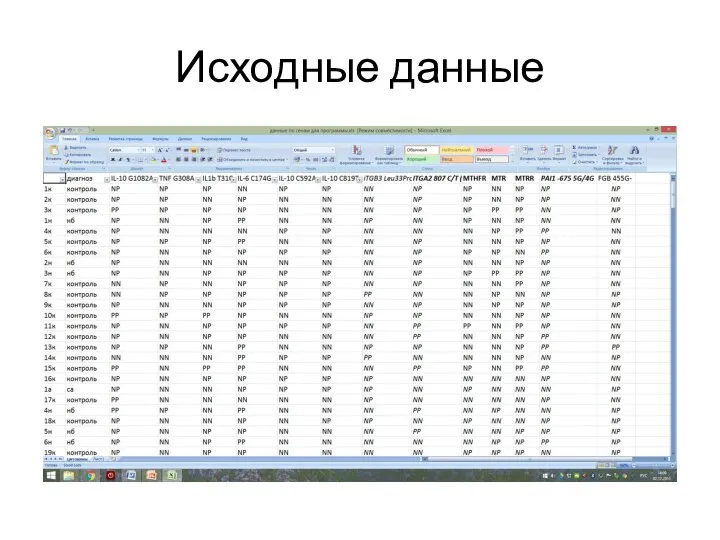
Исходные данные

Оценка риска является задачей классификации, признаковое пространство генетического бесплодия и самопроизвольного прерывания беременности представляет собой множество данных генетических исследований супругов (мужчины У и женщины Х):
а признаковое описание пары принимает вид:
(z1(y),…,z16(y),z1(x),…,z16(x))=(k1(у),…,k4(у),f1(х),…,f3(х),c1(у),…,c5(у) g1(х),…,g4(х),g1(у),…,g4(у),c1(х),…,c5(х),f1(у),…, f3(у),k1(х),…, k4(х)),
где
k1..k4– признаки генов системы контроля клеточного цикла и репарации;
c1..c5– признаки генов цитокинов;
g1..g4– признаки генов системы гемостаза;
f1..f3 –признаки генов фолатного цикла.

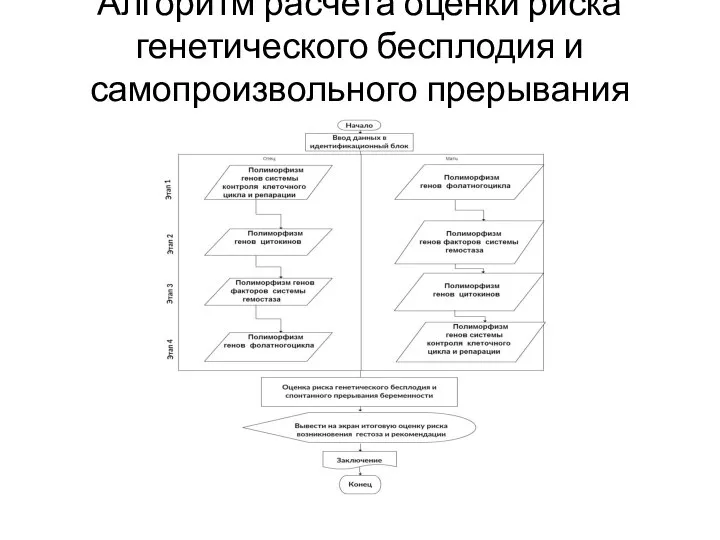
Алгоритм расчета оценки риска генетического бесплодия и самопроизвольного прерывания беременности

1этап: f1(х),…, f3(х), k1(у),…, k4(у);
2 этап: g1(х),…, g4(х),c1(у),…, c5(у);
3 этап: c1(х),…, c5(х), g1(у),…, g4(у);
4 этап: k1(х),…, k4(х), f1(у),…, f3(у).
Алгоритм расчета оценки риска генетического бесплодия и самопроизвольного прерывания беременности

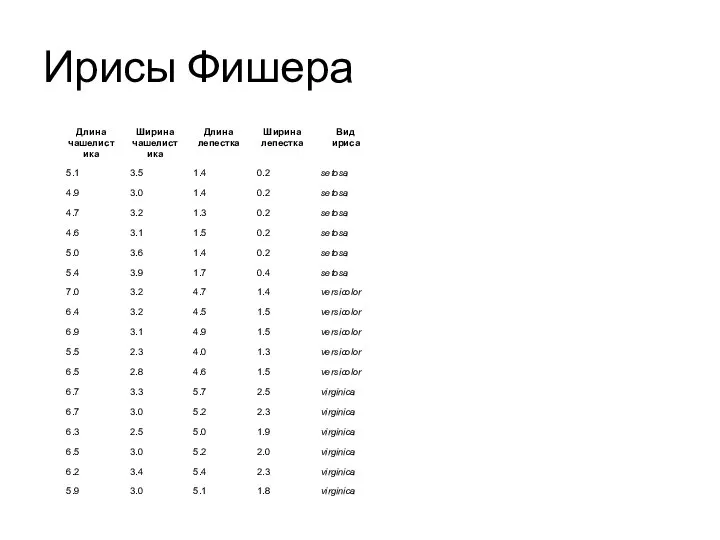
Ирисы Фишера
Ирисы Фишера — это набор данных для задачи классификации, на примере которого Рональд Фишер в 1936 году продемонстрировал работу разработанного им метода дискриминантного анализа. Иногда его также называют ирисами Андерсона, так как данные были собраны американским ботаником Эдгаром Андерсоном. Этот набор данных стал уже классическим, и часто используется в литературе для иллюстрации работы различных статистических алгоритмов.
Ирисы Фишера состоят из данных о 150 экземплярах ириса, по 50 экземпляров из трёх видов — Ирис щетинистый (Iris setosa), Ирис виргинский (Iris virginica) и Ирис разноцветный (Iris versicolor). Для каждого экземпляра измерялись четыре характеристики (в сантиметрах):
Длина наружной доли околоцветника (англ. sepal length);
Ширина наружной доли околоцветника (англ. sepal width);
Длина внутренней доли околоцветника (англ. petal length);
Ширина внутренней доли околоцветника (англ. petal width).
На основании этого набора данных требуется построить правило классификации, определяющее вид растения по данным измерений. Это задача многоклассовой классификации, так как имеется три класса — три вида ириса.
Один из классов (Iris setosa) линейно-разделим от двух остальных.

Ирисы Фишера

Диаграмма рассеяния
ирисов Фишера
«Anderson's Iris data set» участника Indon - собственная работа. Под лицензией CC BY-SA 3.0 с сайта Викисклада - https://commons.wikimedia.org/wiki/File:Anderson%27s_Iris_data_set.png#/media/File:Anderson%27s_Iris_data_set.png

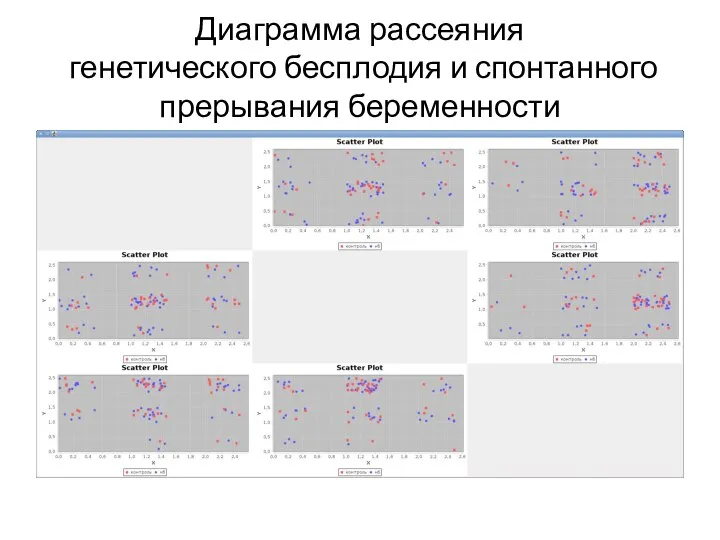
Диаграмма рассеяния
генетического бесплодия и спонтанного прерывания беременности

Визуализация многомерных данных с помощью диаграмм Эндрюса
Дэвид Эндрюс (Andrews, David F.) в 1972-м году описал удобный способ визуализации многомерных данных.
Суть данного метода такова:
Каждая точка представляется в виде тригонометрического ряда Фурье:
Получившаяся функция изображается на графике в промежутке

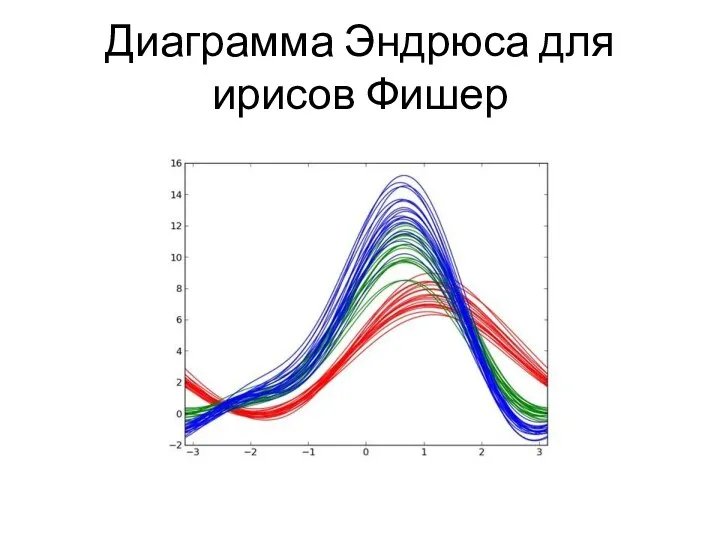
Диаграмма Эндрюса для ирисов Фишер

Анализ признаков xi в осуществляется в порядке убывания их информативности
IDi (x1)> IDi(x2) > IDi(x3) >…. >IDi(xm).

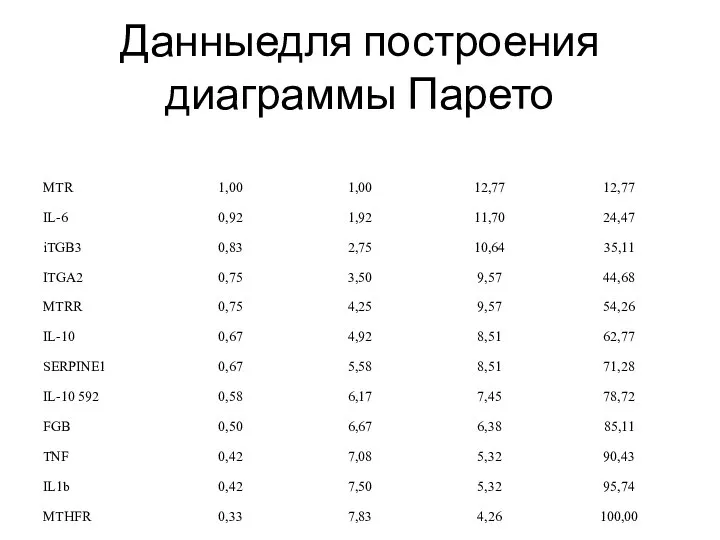
Данныедля построения диаграммы Парето

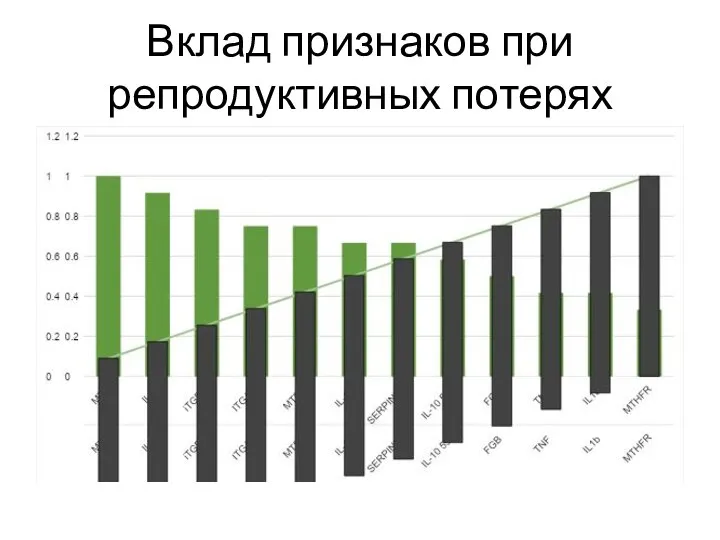
Вклад признаков при репродуктивных потерях

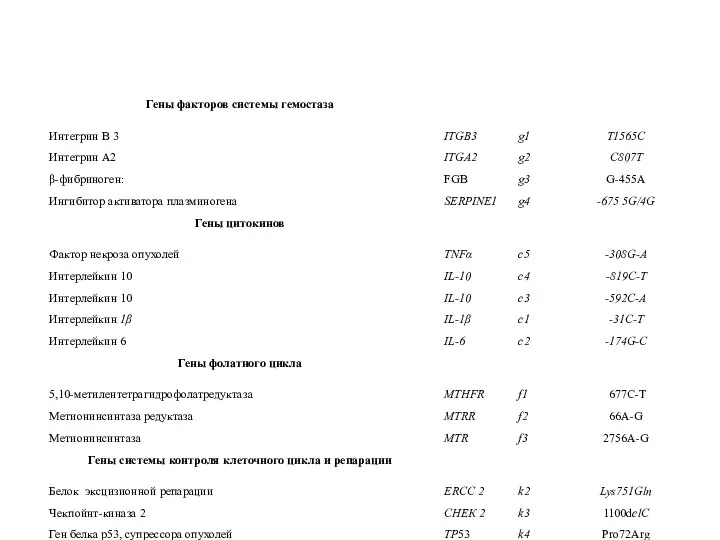
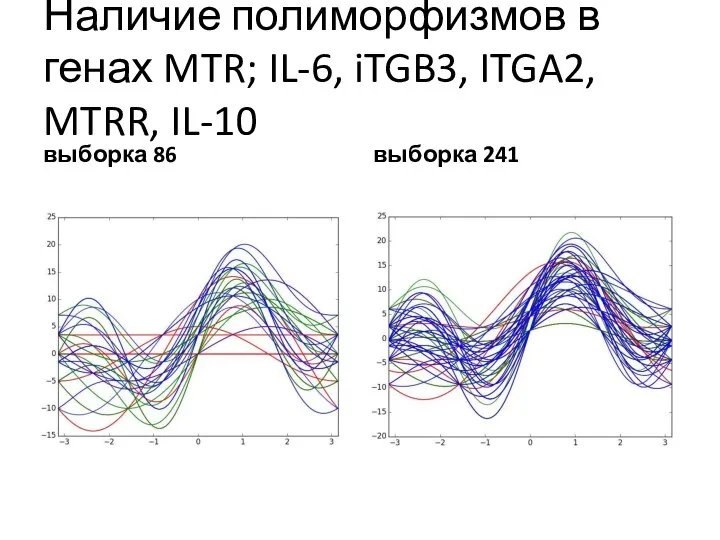
Наличие полиморфизмов в генах MTR; IL-6, iTGB3, ITGA2, MTRR, IL-10
выборка 86
выборка 241

Многослойная искусственная нейронная сеть
Для решения проблемы с линейной неразделимостью образов была предложена двуслойная искусственная нейронная сеть . В качестве архитектуры сети была выбрана сеть с 13 входными нейронами (по количеству признаков), 1 скрытым слоем, содержащим 100 нейронов, и 1 выходным. Классу «0» соответствовал сигнал «0» выходного нейрона, а классу «1» - сигнал «1». В качестве пороговой функции был выбран сигмоид f(x)=1/(exp(-x)+1).
Программная реализация была выполнена на Java с использованием свободной библиотеки neuroph. Чтение исходного файла с выборкой было реализовано с использованием свободной библиотеки supercsv для работы с файлами в формате tsv.
На обучающей выборке число верно классифицированных примеров составило 239 из 240, что составляет 0.99, что является превосходным результатом, но может свидетельствовать о переобучении. Чтобы избежать этого был использован метод перекрестной проверки .

Перекрестная проверка
Исходное обучающее множество было перемешано и разбито на k=10 частей равного размера. Затем последовательно выбиралась каждая из 10 частей и служила проверочным множеством, в то время как остальное множество использовалось для обучения.
Результаты перекрестной проверки приведены.

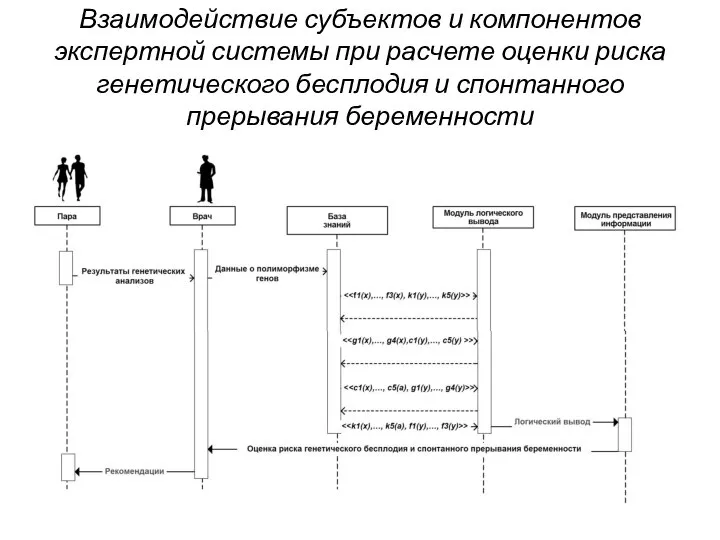
Взаимодействие субъектов и компонентов экспертной системы при расчете оценки риска генетического бесплодия и спонтанного прерывания беременности

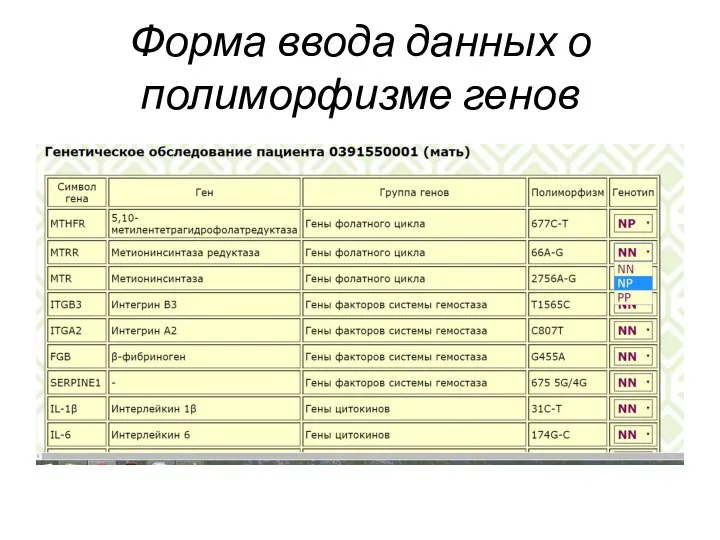
Форма ввода данных о полиморфизме генов