Лечение и понимание результатов исследования. Проверка гипотез

План
Роль случайных факторов
Величина р (пи)
Вероятность того, что существующие различия останутся незамеченными
Внесение поправок на исходные различия
Использование доверительных интервалов при интерпретации результатов клинических исследований
Лечение и понимание результатов исследования: измерение корреляции

Как уже отмечалось на предыдущих занятиях, истинный размер эффекта лечения можно оценить только в ходе эксперимента.

Для более точной оценки истинного эффекта лечения исследователи применяют различные статистические методы.
Статистические методы используются главным образом для проверки той или иной гипотезы, начиная с нулевой гипотезы, которую нужно рассмотреть и, возможно, опровергнуть.
Как правило, нулевая гипотеза предполагает отсутствие различий между сравниваемыми методами лечения.
В рандомизированных контролируемых испытаниях (РКИ), в которых сравнивается эффективность изучаемого метода лечения и плацебо, нулевая гипотеза будет звучать так: истинное различие по частоте наступления определенного клинического исхода в основной и контрольной группах отсутствует (т.е. равно 0).

При проверке гипотезы статистический анализ призван ответить на вопрос, соответствуют ли полученные данные нулевой гипотезе.
Логика подобного подхода такова: даже если изучаемое лечение в действительности не оказывает ни положительного ни отрицательного влияния на клинические исходы (т.е. его эффективность равна 0), результаты, полученные в основной и контрольной группах, редко совпадают полностью.
Чем больше различаются полученные данные, тем менее достоверна нулевая гипотеза.
В случае получения значительных различий между группами лечения и контроля исследователи вправе от нее отказаться.

Роль случайных факторов
При сравнении одинаково эффективных препаратов частота наступления того или иного клинического исхода в 2 группах может также оказаться различной под влиянием случайных факторов.
Статистическая обработка данных направлена на определение степени, в которой подобные различия можно объяснить влиянием случайных факторов, а в каких случаях необходимо искать другие причины (например, большая или меньшая эффективность того или иного метода лечения).
Результаты статистического анализа в большой мере зависят от размера выборки.

ВЕЛИЧИНА Р
При сравнении двух методов лечения исследователи задаются вопросом: ≪Какова вероятность того, что наблюдаемые различия обусловлены только влиянием случайных факторов?≫
Если принять р<0,05 (для биомедицинских исследований), следует отвергнуть нулевую гипотезу и сделать вывод о большей (или меньшей) эффективности изучаемого вмешательства, когда при проведении эксперимента такие же или более выраженные различия будут наблюдаться менее чем в 5% случаев.
Исследователь может ошибочно предположить, что между группами лечения и контроля существуют различия, хотя на самом деле они отсутствуют. Согласно статистической терминологии, подобные ошибки называют ошибкой I рода (а-ошибкой), а их вероятность соответствует уровню а.

Пример
В результате проведенного РКИ, в котором сравнивали эффективность эналаприла и гидралазина в сочетании с нитратами у 804 мужчин с сердечной недостаточностью, получены следующие данные.
В течение периода наблюдения от 6 мес. до 5,7 года в группе эналаприла умерли 132 из 403 (33%) больных, а в группе гидралазина 153 из 401 (38%) больных.
При сравнении полученных результатов (доли умерших больных) с помощью статистического критерия хи-квадрат Пирсона было показано, что если нулевая гипотеза верна (т.е. уровень смертности в обеих группах одинаков), то указанные или более выраженные различия между группами могут встретиться в 11 из 100 случаев (р=0,11). Таким образом, приняв за точку разделения величину р<0,05, мы не можем отвергнуть нулевую гипотезу и вынуждены считать, что наблюдаемые различия случайны.

Некоторые врачи могут прокомментировать полученные результаты следующим образом: ≪Нулевую гипотезу отвергнуть нельзя (так как р>0,05), однако нельзя утверждать, что эналаприл не более эффективен, чем комбинированная терапия (гидралазин в сочетании с нитратами). Полученные результаты все же неубедительны≫.

ВЕРОЯТНОСТЬ ТОГО, ЧТО СУЩЕСТВУЮЩИЕ РАЗЛИЧИЯ
ОСТАНУТСЯ НЕЗАМЕЧЕННЫМИ
Исследование показало, что прием эналаприла все же снижает уровень смертности на 5% (38%-33%) по сравнению с применением вазодилататоров (гидралазин в сочетании с нитратами).
Если бы различие по уровню смертности на самом деле составляло 5%, следовало бы сделать заключение, что эналаприл имеет важные преимущества.
Несмотря на это, мы вынуждены придерживаться нулевой гипотезы, так как различия между группами статистически незначимы (р>0,05).

Почему же исследователи, наблюдая такие различия по уровню смертности, не могут сделать вывод о том, что эналаприл эффективнее гидралазина в сочетании с нитратами?
Потому что число участников исследования было недостаточным для подтверждения истинности этих различий.
Вероятность того, что клинически значимые различия останутся незамеченными (иначе, вероятность возникновения ошибки II рода – не обнаружить различия там, где на самом деле они существуют), уменьшается по мере увеличения размера выборки.
Чем больше выборка, тем меньше риск совершения ошибки II рода и тем выше его статистическая мощность.

Поэтому следует различать статистическую и клиническую значимость результатов исследования.
Следует учитывать, что чем более выражены (хотя и статистически незначимые) различия между группами лечения и контроля, тем выше вероятность того, что истинный эффект терапии остался незамеченным.

ВНЕСЕНИЕ ПОПРАВОК НА ИСХОДНЫЕ РАЗЛИЧИЯ
В процессе рандомизации больные распределяются случайным образом; при этом, как правило, формируются сопоставимые группы.
Другой способ поправки исходных различий между группами сравнения – это расчет стандартизованных показателей.

При проверке гипотез определяют вероятность того, что наблюдаемые результаты случайны, если верна нулевая гипотеза, т.е. гипотеза, согласно которой чаще всего подразумевается отсутствие различий между основной и контрольной группами.
Если вероятность наблюдаемых различий менее 5% (р<0,05), то нулевая гипотеза отвергается, т.е. различия между группами есть.

Все больше авторов медицинских исследований и преподавателей медицинских дисциплин понимают ограничения проверки гипотез; теперь становится более популярным альтернативный подход к сравнению данных, полученных в группах сравнения, а именно расчет точечных значений и доверительных интервалов (ДИ).

ТРУДНОСТИ ПРИ ИНТЕРПРЕТАЦИИ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ.
Вернемся к примеру
Авторы двойного слепого рандомизированного контролируемого испытания (РКИ), в котором участвовали 804 мужчины с сердечной недостаточностью, сравнивали применение эналаприла и лечение гидралазином в сочетании с нитратами. За период наблюдения, длительность которого составила от 6 мес до 5,7 года, умерли 132 из 403, или 33%, больных в группе эналаприла, и 153 из 401, или 38%, больных в группе комбинированного лечения. Величина р, характеризующая статистическую значимость различий по смертности между группами, составила 0,11.

Если согласиться с рекомендуемым значением вероятности того, что наблюдаемые различия обусловлены влиянием случайных факторов (р>0,05), нулевую гипотезу отвергать нельзя, т.е. можно заключить, что между группами сравнения не было существенных различий. Исследователи также провели анализ, в ходе которого помимо выживаемости сравнивали сроки наступления смерти в группах. В результате такого анализа дожития, который в целом более чувствителен, чем оценка различий по частоте развития клинического исхода, была рассчитана величина р=0,08 (что указывает на отсутствие статистически значимых различий между группами). Это подтвердило результаты более простого анализа.

Вместе с тем авторы сообщают о том, что различие по уровню смертности между группами через 2 года (который рассматривался в качестве одного из основных критериев оценки) достигло уровня статистической значимости (р=0,016). Подобные противоречия способны запутать любого. На этом этапе врач должен спросить себя, указывают ли результаты исследования на преимущества эналаприла - ингибитора ангиотензинпревращающего фермента (АПФ)-перед гидралазином в сочетании с нитратами, либо на отсутствие различий между двумя вмешательствами.

РЕШЕНИЕ ПРОБЛЕМЫ: ЧТО ТАКОЕ ДОВЕРИТЕЛЬНЫЕ
ИНТЕРВАЛЫ?
Доверительный интервал представляет собой интервал значений, рассчитанный для какого-либо параметра по выборке и с определенной вероятностью (в медицине, как правило, 95%), включающий истинное значение этого параметра во всей генеральной совокупности
Для нашего примера абсолютное различие по смертности равно 5%, а 95% ДИ значений этого показателя составляет от -1,2 до 12%

Как теперь можно интерпретировать результат исследования?
Наиболее вероятное различие по смертности равно 5%, хотя истинное значение может оказаться в непосредственной близости от -1,2% (т.е. комбинированная терапия гидралазином и нитратами уменьшает смертность на 1,2% по сравнению с применением ингибиторов АПФ) или от 12% (ингибиторы АПФ более эффективны, чем комбинированная терапия).
Чем дальше предполагаемая величина от точечного значения (5%), тем менее она вероятна. Можно заключить, что продолжительность жизни у больных, принимающих ингибиторы АПФ, скорее всего выше, чем на фоне приема гидралазина в сочетании с нитратами; но эти различия могут быть несущественными или же, напротив, весьма значительными.
Можно сделать вывод о том, что при прочих равных условиях ингибитор АПФ более эффективен при сердечной недостаточности, чем гидралазин в сочетании с нитратами, однако доказательства того малоубедительны.

На окончательное решение повлияют данные о токсичности и стоимости препарата, а также результаты других исследований.
Поскольку в нескольких крупных РКИ было показано снижение смертности на фоне приема ингибиторов АПФ при сердечной недостаточности, можно с уверенностью рекомендовать препараты этого фармакологического класса как средство выбора у таких больных.
Найти и читать: GargR YusufS. Overview of randomized trials of angiotensin-converting enzyme inhibitors on mortality and morbidity in patients with heart failure Collaborative Group on ACE Inhibitor Trials JAMA 1995 273 1450-1456.

Из этого примера видно, что при оценке результатов исследований, следует обратить внимание на верхнюю границу ДИ, которая характеризует наибольшую возможную эффективность изучаемого вмешательства.
Если верхняя граница ДИ исключает какой-либо существенный эффект лечения, можно смело утверждать, что польза сравниваемых методов одинакова. Если, напротив, ДИ включает значения, соответствующие клинически значимому эффекту изучаемого вмешательства, нельзя отрицать его преимущества.

Подобный подход к интерпретации результатов исследований, в которых выявляют различия между основной и контрольной группами с использованием ДИ, крайне полезен, когда надо определить, нужно ли заменять существующее вмешательство новым, которое дешевле, проще или менее токсично.
Результаты исследований эквивалентности вмешательств свидетельствуют о целесообразности такой замены, только если обычное лечение не обладает существенными дополнительными преимуществами по сравнению с менее дорогостоящим или более простым.
Мы будем уверены, что исключили вероятность наличия существенной дополнительной пользы стандартного лечения, если верхняя граница ДИ вокруг точечного значения размера эффекта ниже порога клинической значимости.

В другом двойном слепом РКИ с участием больных с сердечной недостаточностью сравнивали эффективность эналаприла и плацебо.
Из 1285 больных в группе эналаприла умерли или были госпитализированы в связи с сердечной недостаточностью 613 (48%), а из 1284 больных в группе плацебо — 736 (57%).
Точечное значение различия по комбинированному показателю смертности и частоты госпитализаций в связи с сердечной недостаточностью составляет 10% при 95% ДИ от 6 до 14%.
Наименьший возможный эффект эналаприла в данном случае заключается в уменьшении частоты развития неблагоприятных исходов на 6%, что соответствует ЧБНЛ, равному 17.
Если вы считаете такой размер эффекта клинически значимым, выборка достаточна, в противном случае необходимо проведение более крупного исследования (с более узкими ДИ значений размера эффекта).
Ссылка на источник: The SOLVD Investigators Effect of enalapnl on survival in patients with reduced left ventricular ejection fractions and congestive heart failure N Engl J Med 1991,325 293—302

Выводы по ДИ
Если в исследовании были выявлены различия между группами сравнения, следует обратить внимание на нижнюю границу ДИ, чтобы определить, был ли достаточным размер выборки.
Если эта нижняя граница, которая соответствует наименьшему возможному эффекту лечения при правдоподобности полученных результатов, выше порога клинической значимости, размер выборки достаточен; поэтому проведения дополнительных РКИ не требуется. Если же нижняя граница ДИ не достигает этого порога, размер выборки недостаточен, и необходимо проведение новых, более крупных РКИ.

Выводы по ДИ
В случае с исследованием, в котором не было показано различий между группами сравнения, обратите внимание на верхнюю границу ДИ, чтобы определить, достаточное ли количество больных участвовало в исследовании.
Если эта верхняя граница, которая соответствует наибольшему возможному эффекту лечения при правдоподобности полученных результатов, не достигает порога клинической значимости, размер выборки достаточен; поэтому проведения дополнительных РКИ не требуется. Если же верхняя граница ДИ выше этого порога, размер выборки недостаточен, и необходимо проведение новых, более крупных РКИ.

Измерение корреляции
Врачи изучают результаты клинических испытаний, чтобы оценить связь между лечением и клиническим исходом.
В ходе исследования такая связь может быть подтверждена или отвергнута; например, полученные результаты могут свидетельствовать о том, что изучаемое вмешательство уменьшает риск развития осложнений или, напротив, не влияет на него.

Информацию о корреляции между вмешательством и клиническим исходом получают, измерив
относительный риск (ОР),
снижение относительного риска (СОР),
снижение абсолютного риска (САР),
отношение шансов (ОШ),
число больных, которых необходимо лечить определенным методом в течение определенного времени, чтобы достичь определенного благоприятного эффекта или предотвратить определенный неблагоприятный исход у одного больного (ЧБНЛ), или индекс потенциального вреда (ИПВ).

Дихотомические и непрерывные данные
Основой для первичного анализа обычно служат данные о доле участников в группах контроля и вмешательства, у которых выявлен тот или иной клинический исход.
В качестве благоприятных или неблагоприятных клинических исходов могут быть выбраны наличие или отсутствие инсульта, инфаркта миокарда, метастазов злокачественных опухолей, смерть или выживание, заживление язвы или исчезновение симптомов (это дихотомические данные: «есть» или «нет»).
Количественные данные (число приступов стенокардии в месяц, частота обращений в отделение неотложной помощи, лабораторные показатели) обычно представляют в виде средних величин в группах сравнения.

Количественные данные можно преобразовать в дихотомические, если определить пороговые значения или степень изменения, отражающую существенное улучшение или ухудшение состояния, с последующим подсчетом доли участников, у которых был достигнут означенный порог или отмечались соответствующие изменения.

ТАБЛИЦА СОПРЯЖЕННОСТИ

Пример РКИ
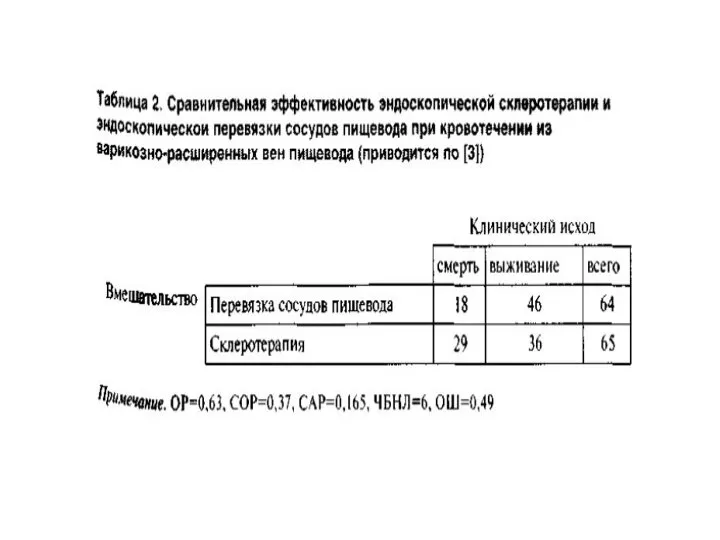
Предположим, что в рандомизированном контролируемом испытании (РКИ) оценивали смертность при кровотечении из варикозно-расширенных вен пищевода после их эндоскопической перевязки по сравнению с эндоскопической склеротерапией. Средняя продолжительность наблюдения составила 10 мес; к концу испытания в группах перевязки сосудов и склеротерапии умерли 18 из 64 и 29 из 65 больных соответственно.

АБСОЛЮТНЫЙ РИСК
Определение абсолютного риска (АР) служит наиболее простым способом оценки связи между вмешательством и исходом.
АР смерти в группе перевязки сосудов пищевода составляет 28% (18 из 64 больных, или а/a+b), а в группе склеротерапии — 45% (29 из 65 больных, или c/c+d).
Риск развития неблагоприятного исхода в контрольной группе обычно называют исходным риском, или частотой развития исхода в контрольной группе.

СНИЖЕНИЕ АБСОЛЮТНОГО РИСКА
Величины АР можно соотнести путем определения разницы между ними. Этот показатель получил название САР; он рассчитывается по формуле:
с/(с+ d)—а/(а+b)
и позволяет оценить, насколько реже тот или иной неблагоприятный исход наступает в основной группе по сравнению с контрольной. В нашем примере САР=0,446-0,281=0,165 или 16,5%.

ОТНОСИТЕЛЬНЫЙ РИСК
Другой способ оценки связи между величинами АР заключается в определении отношения между ними, т.е. ОР, или отношения риска. Этот показатель позволяет судить, во сколько раз изменилась вероятность клинического исхода в группе изучаемого вмешательства (в нашем примере эндоскопической перевязки сосудов пищевода) по сравнению с контрольной группой (склеротерапии).
ОР рассчитывают по формуле:
[a/(a+ b)]/[с/(с+d)]
В рассмотренном примере в группе перевязки умерли 18 из 64 больных, а в группе склеротерапии — 29 из 65, т.е. ОР=63%.
Другими словами, АР смерти при перевязке сосудов пищевода примерно в 1,6 раза, ниже, чем при склеротерапии.

СНИЖЕНИЕ ОТНОСИТЕЛЬНОГО РИСКА
Оценить эффективность вмешательства можно и с помощью СОР, которое отражает уменьшение исходного риска в группе изучаемого вмешательства и рассчитывается путем деления САР на АР в контрольной группе.
В нашем примере для определения СОР необходимо 16,5% (САР) разделить на 44,6% (АР смерти в группе склеротерапии); таким образом, СОР составляет 0,37.
СОР можно подсчитать и другим способом: 1,0—ОР; в рассмотренном случае 1,0-0,63=0,37 или 37%.
Т.о., эндоскопическая перевязка сосудов пищевода по сравнению со склеротерапией сопровождается уменьшением риска смерти на 37%.

ОТНОШЕНИЕ ШАНСОВ
Вместо оценки риска возникновения того или иного клинического исхода мы можем определить отношение шанса его развития к шансу того, что он не возникнет.
В медицинских исследованиях ОШ определяется как отношение доли участников исследования, у которых выявлен тот или иной клинический исход, к доле больных, у которых данный исход не развился.
В большинстве случаев шансы и ОР приблизительно равны, поэтому многие авторы, фактически рассчитывая ОШ, представляют полученные результаты в виде ОР.
Такое толкование может приводить к ошибочным выводам.

Рассмотрим следующий пример. Предположим, что у 20% больных, включенных в испытание, развился инсульт; следовательно, шанс составляет (1/5)/(4/5) или 0,20/0,80=0,25.

В нашем примере для расчета шансов смерти в группе перевязки сосудов пищевода следует разделить 18 (число умерших) на 46 (число выживших), а в группе склеротерапии — 29 на 46.
ОШ определяется по формуле (а / b) / (с / d) = (18 / 46) / (29 / 36) = 0,49.
Подобно тому, как отношение показателей риска получило название ОР, найденное значение можно было бы назвать относительными шансами, однако эпидемиологи, не склонные к аналогиям, предпочли другой термин, а именно отношение шансов.

Любой врач, наверное, предпочел бы заменить несколько расплывчатое ОШ интуитивно понятным показателем ОР.
Для такой замены необходимо, чтобы значение ОР = [а / (а + b)] / [с / (с + d)] было близко к значению ОШ = (а / b) / (с / d).
Это условие будет соблюдено, если «а» будет значительно меньше, чем «b», а «с» значительно меньше, чем «d»; другими словами, если частота изучающегося исхода в обеих группах будет небольшой.
По мере уменьшения ОР его величина приближается к значению шансов. В большинстве РКИ частота развития изучаемого клинического исхода достаточно мала, поэтому значения ОР и ОШ практически совпадают. Аналогично показатели ОР и ОШ окажутся почти одинаковыми, если размер эффекта лечения невелик (т.е. ОР и ОШ приблизительно равны 1), но при выраженном эффекте эти показатели различаются.

Чтобы лучше понять взаимосвязь между ОР, ОШ и САР, несколько видоизменим нашу таблицу сопряженности.
Предположим, что смертность в обеих группах уменьшилась приблизительно на 50%, т.е. в группе перевязки сосудов умерли 9 из 64 больных, а в группе склеротерапии — 14 из 65.
АР смерти при этом снизился с 28 до 14% в группе перевязки сосудов и с 44,6 до 21,5% в группе склеротерапии.
ОР составляет 14 / 21,5 = 0,65 (почти не отличается от ранее 0,63).
ОШ равняется (9 / 55) / (14 / 51) или 0,60, что несколько отличается от прежнего значения (0,49) и приближается к показателю ОР.
Значение же САР изменилось кардинально — с 16,5 до 8% (21,5 % - 14%=8%).
Таким образом, уменьшение смертности в обеих группах в 2 раза не повлияло на ОР, привело к небольшому увеличению ОШ и уменьшению САР в 2 раза.
Данный пример показывает, что ОР может быть одинаковым при различных показателях САР; и в то время как ОР не дает никакой информации о риске развития неблагоприятного исхода в контрольной группе (в нашем примере в группе менее эффективного лечения), САР в значительной степени зависит от исходного АР.

ЧИСЛО БОЛЬНЫХ, КОТОРЫХ НЕОБХОДИМО ЛЕЧИТЬ
Эффект вмешательства можно выразить и при помощи подсчета числа больных, которых необходимо лечить, чтобы предотвратить определенный неблагоприятный исход у одного больного (ЧБНЛ)

Смертность в группе перевязки сосудов пищевода составляет 28,1%, а в группе склеротерапии — 44,6%.
На нашем примере мы можем сказать, что перевязка сосудов у 100 больных позволяет предотвратить 16 дополнительных смертей по сравнению со склеротерапией (при таком размере выборки этот показатель равен САР, т.е. разнице между частотой развития клинического исхода в контрольной и основной группах: 44,6-28,1=16,5).

Если проведение лечения 100 больным способствует увеличению числа выживших на 16, скольких больных необходимо лечить, чтобы избежать одной смерти?
Для ответа на этот вопрос разделим 100 на 16 (САР в %) и получим ЧБНЛ, приблизительно равное 6.
Данное значение можно определить и другим способом, а именно как величину, обратную САР (в виде дроби), по формуле
1 / САР