Как подготовиться к олимпиадам?

План вебинара
История перечневых олимпиад и зачем они нужны
Подробное описание олимпиад всех уровней
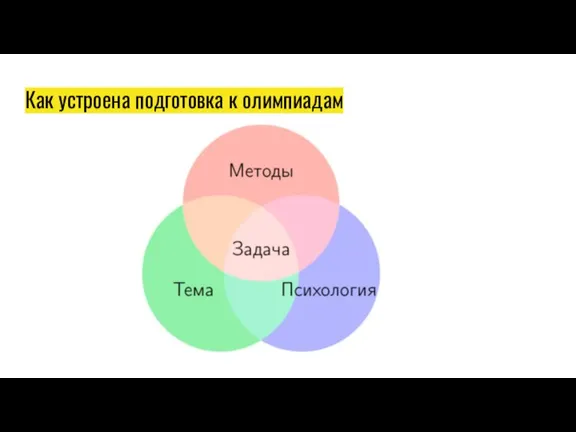
Как устроена подготовка к олимпиадам
Как участвовать в олимпиадах
Пример разбора задач. Как проходит занятие
Ответы на вопросы

Виды олимпиад и их особенности
Всероссийская олимпиада. Предназначена в первую очередь не для поступления, а для спортивного состязания.

Виды олимпиад и их особенности
Для интереса («Медвежонок», «Кенгуру» и тому подобное).

Виды олимпиад и их особенности
Перечневые олимпиады (Высшая Проба, Физтех, Ломоносов, ОММО ….., очень много их).

Виды олимпиад и их особенности
Перечневые олимпиады, являющиеся спортивными по содержанию. Олимпиада СПбГУ, Высшая Проба, Турнир Городов, ММО, Петербургская олимпиада школьников – они все первого уровня.

История перечневых олимпиад. 3 этапа
Можно приближённо выделить три этапа:
Примерно около 2005-2007-х годов олимпиады были в основном при конкретных вузах и давали льготы только в конкретный вуз.
Система совершенствовалась, ввели уровни олимпиад – вузы выбирали, какую льготу даёт какой уровень олимпиады.
Вузы стали больше выбирать не только уровень олимпиады, но и сами конкретные олимпиады (последние годы).

Особенности перечневых олимпиад
Формально соответствует школьной программе.
Разнообразие критериев оценивания.
Уровни и правила поступления. Виды льгот: БВИ, 100 баллов по предмету, дополнительные бонусные баллы.
Процент призеров и победителей от общего числа участников заключительного тура – 15% -25 %, только победителей – около 5% и меньше.

Олимпиады МГУ: ПВГ, Ломоносов
Огромное сходство с ДВИ и бывшими вступительными в МГУ.
Очень важно правильно оформлять, хорошо обосновывать каждый шаг решения, сильно снижают баллы.
При составлении этих олимпиад можно увидеть очень много использования идей задач старых вступительных.
Преобладают абитуриентские темы, олимпиадные темы выражены очень слабо.
Очень хорошая организация олимпиад (строгий контроль).

ПВГ
Сложный отборочный этап (есть творческое задание и тест).
Заключительный тур состоит из 5 равноценных задач. Максимальный балл за олимпиаду – 100. Длительность очного тура составляет 3 часа.
За каждую задачу дают от 0 до 20 баллов. Простота задач компенсируется достаточно жесткими критериями.
Для того, чтобы получить диплом призера, нужно набрать минимум 75 баллов (бывает и 90). На диплом победителя, в свою очередь, нужно набрать 95 баллов, иногда 100 баллов.

Олимпиада Ломоносов
На отборочном этапе нужно набрать много баллов (около 90 % от максимально возможного количества), есть сложные задачи.
На заключительном этапе предлагается решить 7 задач.
Обычно за каждую задачу дают до 15 баллов (плюс – 15 баллов, плюс-минус – 10 баллов, минус-плюс – 5 баллов).
Максимум, который можно получить на олимпиаде – 100 баллов.
Обычно для призёра нужно 60-70 баллов, победителя – от 80.

Высшая проба
Много олимпиадных тем.
У Высшей пробы низкие проходные баллы (дают 7-8 задач, для призёра обычно достаточно решить 2 задачи, победителю – 3).
За каждую задачу возможно получить от 17 до 38 баллов. Система оценивания предоставляет возможность получить какие-то баллы, не имея абсолютно правильного решения.

Олимпиада СПбГУ
Сложная спортивная олимпиада.
На заочном туре вам предоставят 4 задачи и 1 час на их решение.
Длительность очного тура – 4 часа, всего 5 задач, максимум 100 баллов.
Призером можно стать, если набрать чуть больше половины, но это всё равно сложно. Для победителей баллы большие (около 80).

Петербургская олимпиада школьников
Отборочным этапом для этой олимпиады является районный этап ВСОШ. Он проводится в школах Санкт-Петербурга в январе-феврале.
Заключительный этап из года в год проводится в Санкт-Петрбурге и состоит из двух частей: «довывод» и «вывод».
Сначала дается 4 задачи олимпиадного типа и 3 часа времени. Если решить 3 из них, то отведут во вторую аудиторию и дадут оставшиеся ещё 4 задачи вместе с дополнительным часом времени.
Во внимание берутся только полностью решенные задачи. На диплом призера нужно решить 4 задачи, победителя – 7.

ММО (московская математическая олимпиада)
Заключительный тур проводится только в Москве в два дня. Между ними обычно имеется двухнедельный или месячный интервал.
Всего в каждый день дается по 5-6 задач. Если участник не решает двух задач в первый день, на второй день он не приглашается.
Все задачи имеют одинаковый вес – 1 балл.
Олимпиада примечательна тем, что итоговое количество задач считается не по сумме задач, а по их произведению.
Дипломы призёров третьей степени обычно даются за 5 решённых задач. Дипломы призёров второй степени даются за 8 решённых задач. Дипломы победителей даются за 15 решённых заданий.

Турнир городов
Олимпиада состоит из двух туров: осеннего и весеннего.
Каждый тур делится на два варианта: базовый и сложный. Сложный вариант олимпиады сопоставим по трудности с Всероссийской олимпиадой школьников, базовый — несколько проще.
Финальный тур проводится только для 11-классников, получивших диплом победителя в 10 классе (осенью или весной) или на осеннем туре в 11 классе.
Заключительный этап является устным (в то время как отборочный письменный). Для того, чтобы стать призёром, достаточно решить около половины, чтобы победителем - решить почти всё.

Необычные олимпиады
Необычных олимпиад, представляющих уникальные форматы заданий, довольно много, перечислим те, которые дают наибольшие льготы:
Всероссийская олимпиада школьников «Нанотехнологии - прорыв в будущее!» Олимпиада первого уровня.

Необычные олимпиады
Межрегиональная олимпиада школьников имени И.Я. Верченко – олимпиада по криптографии, второго уровня.

Необычные олимпиады
Олимпиада Кружкового движения Национальной технологической инициативы (олимпиада НТИ) – в зависимости от профиля разные уровни олимпиады и разные предметы.

Необычные олимпиады
Олимпиада Ломоносов по механике и математическому моделированию (только в отдельные вузы и специальности) – математика, второй уровень.

Олимпиады второго уровня по математике
Межрегиональная олимпиада школьников им. И.Я. Верченко по математике и криптографии
Межрегиональная олимпиада школьников на базе ведомственных образовательных организаций (межведомственная)
Объединённая межвузовская математическая олимпиада (ОММО)
Объединённая международная математическая олимпиада «Формула Единства»/«Третье тысячелетие»
Олимпиада Курчатов
Физтех
Олимпиада Юношеской математической школы
РосАтом
Турнир Ломоносова
Всесибирская олимпиада

ОММО
В задачах спользуют школьную программу, но не ЕГЭ-ные темы: векторы, координаты, обратные тригонометрические функции, комбинаторика, задачи на рассуждение...
Есть учебное пособие по подготовке к ОММО в интернете.
Проверка работ разбивается на два этапа. Первая проверка проводится в ВУЗах, где участники писали олимпиаду. На вторую проверку обычно проходят те работы, в которых было правильно решено 3 и более задач.
Призёр - 4-5 задач, для победителя обычно 7 хватает (всего задач 10).

Межрегиональная олимпиада школьников
им. И. Я. Верченко по математике и криптографии
На очном этапе дают 6 задач олимпиадного типа среднего и высокого уровня сложности.
Основные темы задач: комбинаторика и целые числа, также необходимо уделить особое внимание основам шифрования. Организаторы олимпиады проводят бесплатную подготовку для всех желающих.
Каждая задача изначально оценивается от 0 до 3 баллов, а затем, с учётом сложности задач, осуществляется перевод в окончательные баллы.
Максимальное количество баллов за работу равно 100.
Для получения диплома призера необходимо набрать 60 баллов (3-4 задачи), победителя – 90 баллов (6 задач).

Олимпиада Физтех
На олимпиаде участникам предлагается решить 6 задач за 4 часа. Все задачи имеют различный вес (в зависимости от сложности). Задачи несложные, очень похожи на ЕГЭ-шные.
Для призёра часто достаточно меньше половины максимального количества баллов набрать (для победителя – немного больше половины). На апелляции часто поднимают баллы.
Первые годы МФТИ продолжал повторять делать свои вступительные, потом добавили немного комбинаторики и теории чисел.

Олимпиада Курчатов
Поздний отборочный этап, заключительный тоже проводится позже, чем у остальных олимпиад.
На очном туре участникам предстоит решить по 6 равновесных задач. Каждая из которых оценивается в 7 баллов.
Для призёра нужно примерно 28 баллов из 42, для победителя 35.
Составляют следующим образом – за основу берут прошлые года олимпиады физтех или вступительных в МФТИ, пытаются из этого собрать спортивную олимпиаду, выбрать наименее стандартные задачи и идеи. Иногда берут с прошлых лет регионального этапа идеи задач.

Всесибирская открытая олимпиада школьников
Отборочный этап проводится в 2 тура: первый очный и второй заочный. Туры независимые, достаточно стать призером или победителем одного, чтобы попасть на заключительный этап.
Заочный тур проводится только для жителей Сибири, это сделано, чтобы в ней участвовало меньше школьников не из Сибири.
Каждая задача оценивается в 7 баллов, максимально возможный балл за работу – 35. Для призёра достаточно решить около половины задач, баллы победителя около 27.

Олимпиада Росатом
Росатом по математике очень похож на олимпиаду Физтех.
На очном туре каждому участнику предлагается 6 задач и 4 часа времени. Задачи не очень сложные, в основном вычислительные.
Все задачи имеют одинаковый вес – 2 балла . Критерии проверки очень строгие: за отсутствие пояснений или за обсчет оценку могут очень сильно снизить.
Многие участники говорят, что, по их мнению, решили олимпиаду очень хорошо, но получили совсем не те баллы, которые ожидали.

Межведомственная олимпиада
На очном этапе участникам предлагается решить 8 задач олимпиадного типа среднего уровня сложности.
Организаторы олимпиады проводят бесплатную подготовку для всех желающих!
Каждая задача изначально оценивается по следующей системе: «-» – 0 баллов, «-+»– 1 балл, «+-» – 2 балла, «+»– 3 балла. Затем, с учётом сложности задач, осуществлялся перевод уже в окончательные баллы для каждой задачи баллы индивидуальные).
Максимальное количество баллов равно 100.

Олимпиада ЮМШ
Заключительный этап традиционно проводится в СПбГУ и состоит из двух частей: «довывод» и «вывод».
Сначала дается 3 сюжета (по 2 задачи в каждом) олимпиадного типа и 2,5-3 часа времени. Каждый сюжет состоит из двух задач схожей тематики.
Если решить 4 задачи, то отведут во вторую аудиторию и дадут оставшиеся задачи вместе с дополнительным часом времени.
Олимпиада устная, то есть решения задач нужно рассказывать члену жюри. По ходу рассказа можно дополнять и исправлять решение, но нужно это делать быстро, иначе засчитывается неверный подход.

Формула Единства
На очном туре вам будет предложено решить 6 равновесных задач. Эта олимпиада больше подходит для абитуриентов, искренне заинтересованных математикой, так как задачи очень сложные.
За каждую задачу дается по 7 баллов, в сумме 42 балла. Оценивают задачи лояльно, часто идут навстречу.
Для призёра обычно достаточно баллов 26, победителя – ближе к 40.

Турнир Ломоносова
Проходит осенью в сентябре-октябре.
В Турнире может поучаствовать любой школьник; задания рассчитаны на учеников 6–11 классов. Состязание многопредметное.
Ученики 10–11 классов, награждённые грамотой турнира, приглашаются на заключительный тур.
Задачи похожи на региональный тур всеросса по математике. Дают 5 задач на 4 часа.
Задачи, за которые выставлены «+» или «±», считаются решёнными и приносят по 1 баллу, остальное просто не учитывается.
Для призёра достаточно 2-3 задачи решить, победителя – все 5.

Как устроена подготовка к олимпиадам

Психология

Подробнее
Надо знать все темы школьной программы. И методы решения.
При подготовке сначала пройти все темы, затем разбирать более сложные задачи по темам и олимпиадные варианты.
В зависимости от вида олимпиады будет разное соотношение прорешивания вступительных прошлых лет / изучения тем.
Нужно тренировать умение распределять время на олимпиаде.
Составить расписание – небольшие порции тем раз в 3-4 дня. По итогам каждой половины недели отмечать, что успел сделать.
Правильно распределить усилия между предметами.
Важна психологическая подготовка – её даёт опыт в олимпиадах. Может помочь психолог или психотерапевт. Многих губит излишняя самоуверенность, или наоборот, страх перед задачами.