Содержание
- 2. 24.11.2017 1. Изменение силы тока I в зависимости от времени t задано уравнением ( I –
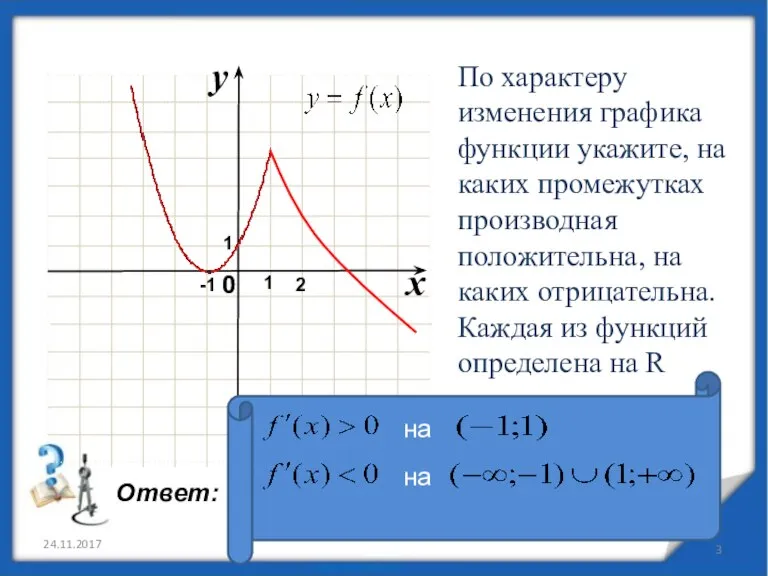
- 3. 24.11.2017 По характеру изменения графика функции укажите, на каких промежутках производная положительна, на каких отрицательна. Каждая
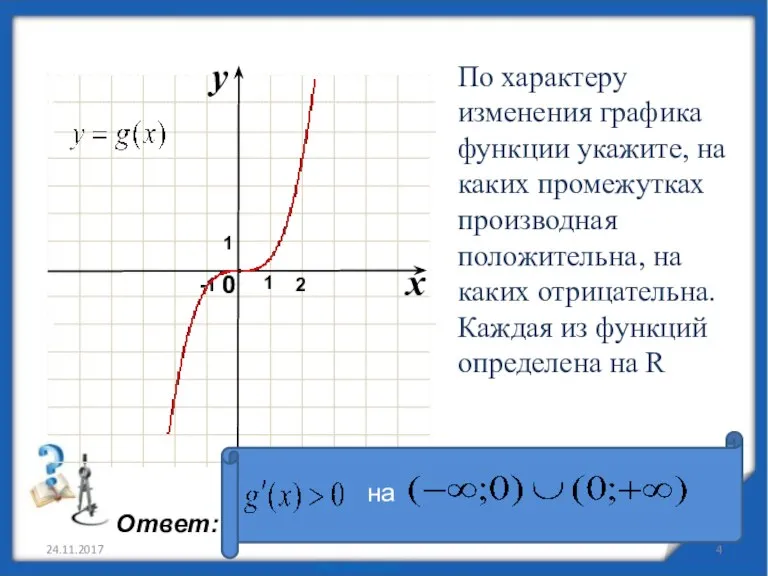
- 4. 24.11.2017 По характеру изменения графика функции укажите, на каких промежутках производная положительна, на каких отрицательна. Каждая
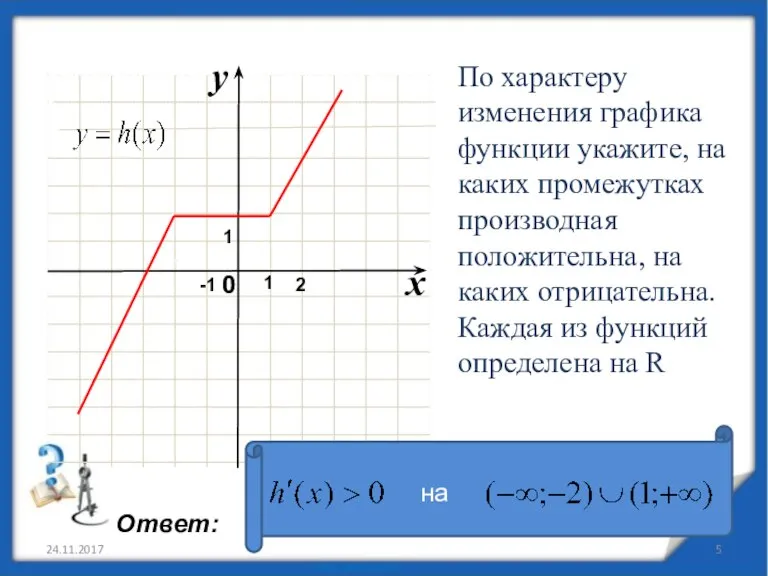
- 5. 24.11.2017 По характеру изменения графика функции укажите, на каких промежутках производная положительна, на каких отрицательна. Каждая
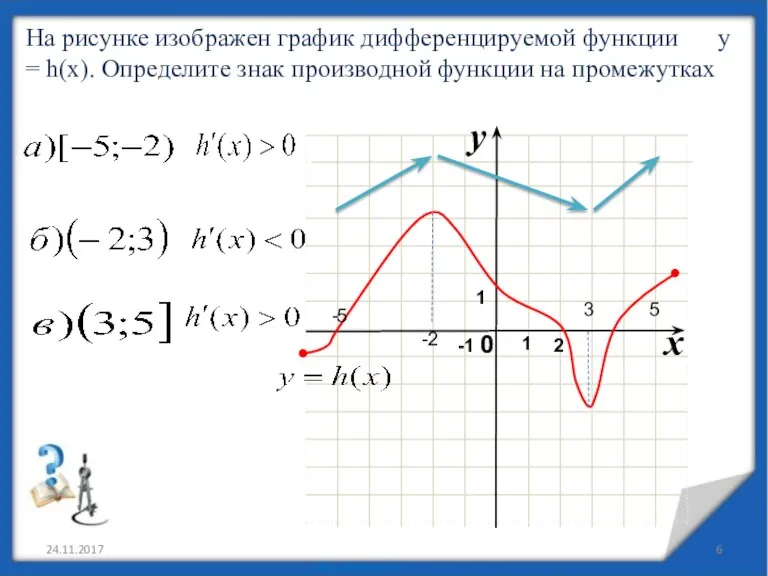
- 6. 24.11.2017 На рисунке изображен график дифференцируемой функции y = h(x). Определите знак производной функции на промежутках
- 7. Дан график производной одной из перечисленных функций. Определите какой? 24.11.2017 Верно Подумай Подумай Подумай Подумай 1
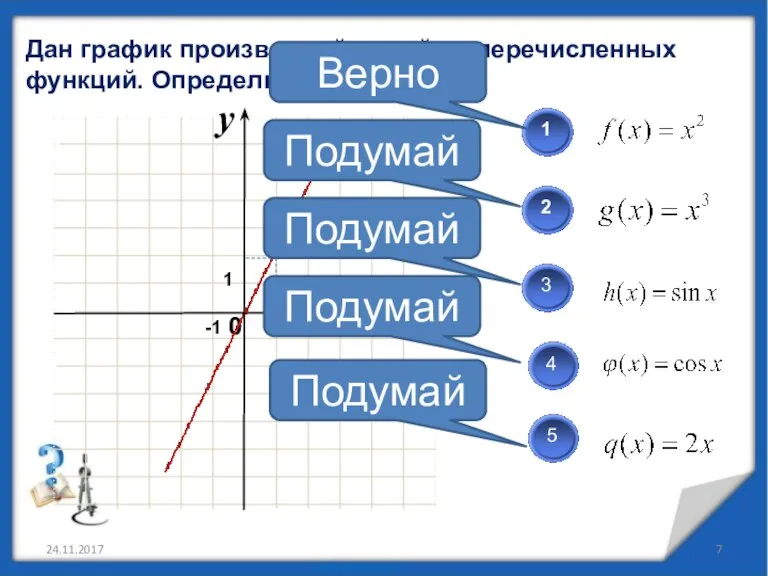
- 8. Дан график производной одной из перечисленных функций. Определите какой? 24.11.2017 Верно Подумай Подумай Подумай Подумай 1
- 9. Дан график производной одной из перечисленных функций. Определите какой? 24.11.2017 Подумай Подумай Подумай Верно Подумай 1
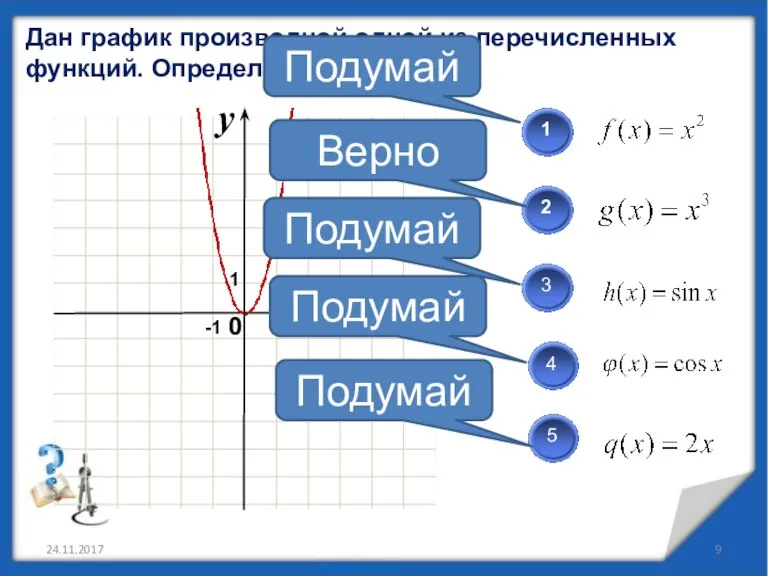
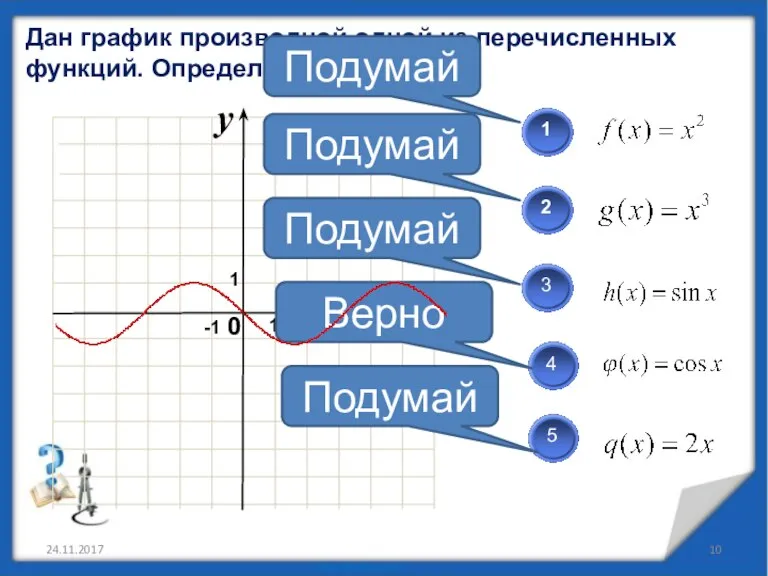
- 10. Дан график производной одной из перечисленных функций. Определите какой? 24.11.2017 Подумай Подумай Подумай Подумай Верно 1
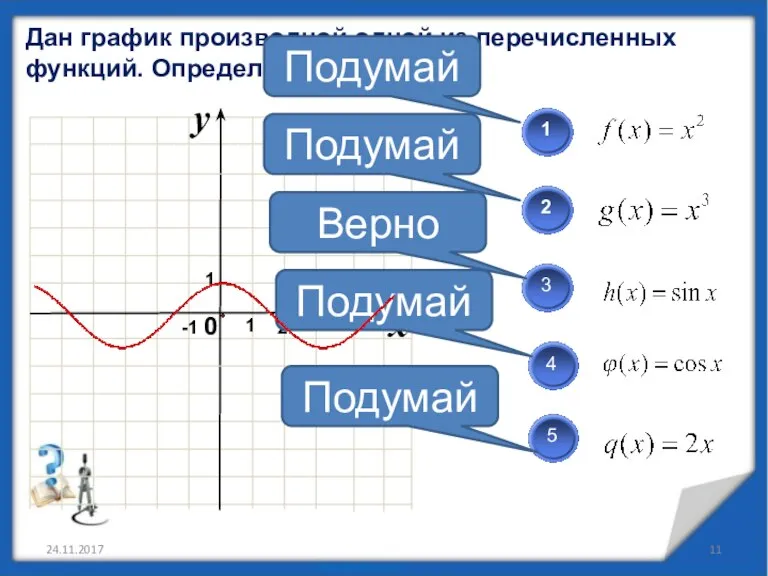
- 11. Дан график производной одной из перечисленных функций. Определите какой? 24.11.2017 Подумай Подумай Подумай Подумай Верно 1
- 12. 24.11.2017 Функция f(x) задана на [a; b]. Определите max и min функции, и точки локального экстремума
- 13. 24.11.2017 Л.Н.Толстой «Много ли человеку земли надо?» …Крестьянин Пахом очень мечтал о собственной земле и собрал
- 14. 24.11.2017 А В С D 2 13 10 15 P = AB + BC + CD
- 15. 24.11.2017 Начертите четырехугольник с периметром 40 км и наибольшей площадью 1 ряд 2 ряд 3 ряд
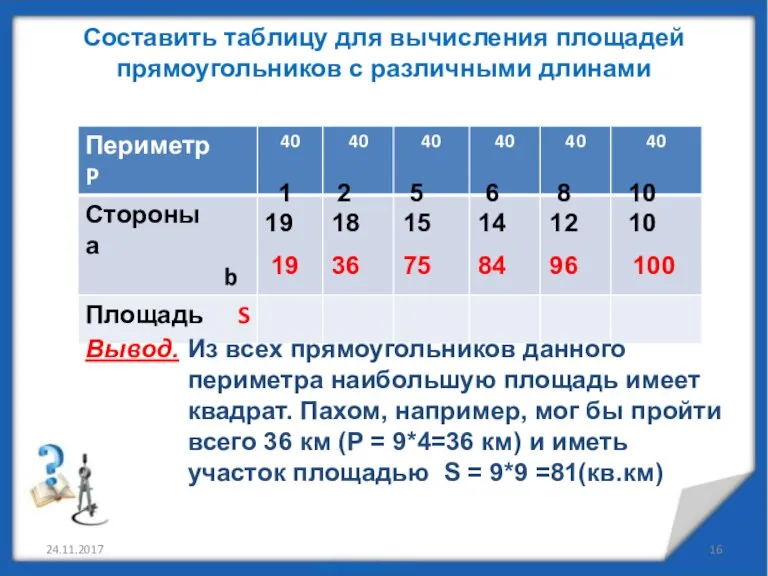
- 16. 24.11.2017 Составить таблицу для вычисления площадей прямоугольников с различными длинами 1 19 19 100 2 18
- 17. 24.11.2017 Схема исследования на наибольшее и наименьшее значения функции 1. Ввести переменную х, от значения которой
- 18. 24.11.2017 В круг радиуса а вписать прямоугольник наибольшей площади. А В С D x O a
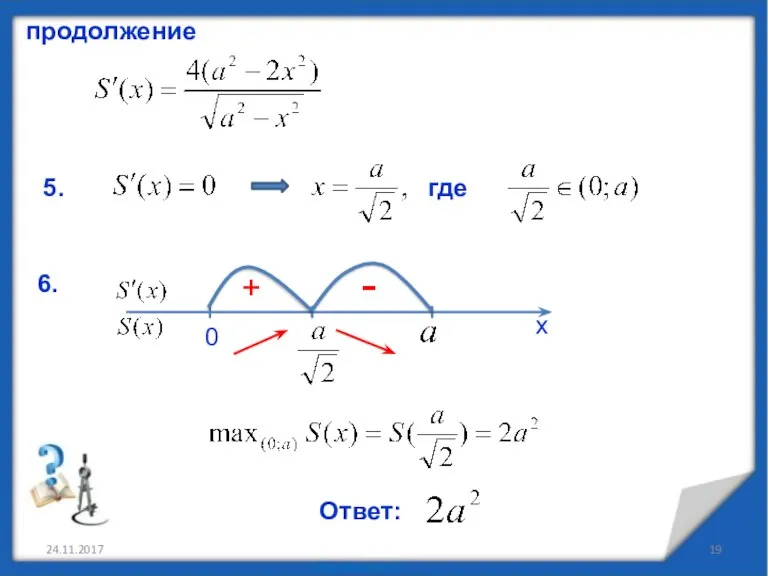
- 19. 24.11.2017 продолжение 5. где 6. х 0 + -
- 20. 24.11.2017 А В С D х 20 - х Наибольшую ли площадь при данном периметре (40
- 21. 24.11.2017 Если бы Пахом при Р=40 км, пробежал бы по периметру квадрата, то площадь была бы
- 22. 24.11.2017 Задача 5.100 В некотором царстве, в некотором государстве подорожала жесть, идущая на изготовление консервных банок.
- 23. 24.11.2017 продолжение на интервале (0; +∞) на интервале (0; +∞) функция имеет единственную критическую точку х1
- 24. 24.11.2017 продолжение Ответ:
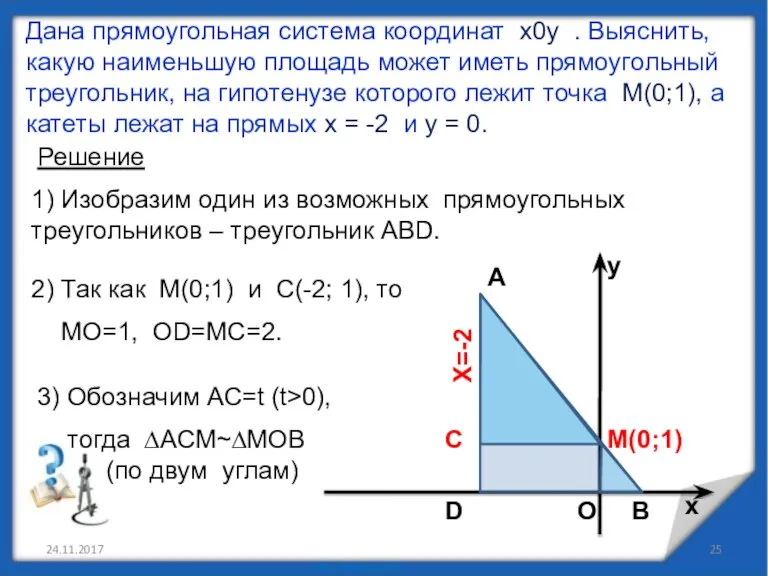
- 25. 24.11.2017 Дана прямоугольная система координат х0у . Выяснить, какую наименьшую площадь может иметь прямоугольный треугольник, на
- 26. 24.11.2017 Дана прямоугольная система координат х0у . Выяснить, какую наименьшую площадь может иметь прямоугольный треугольник, на
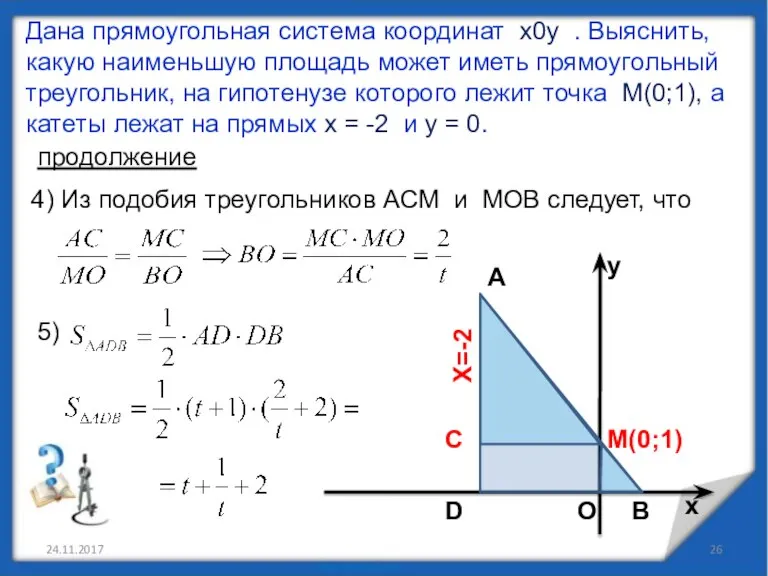
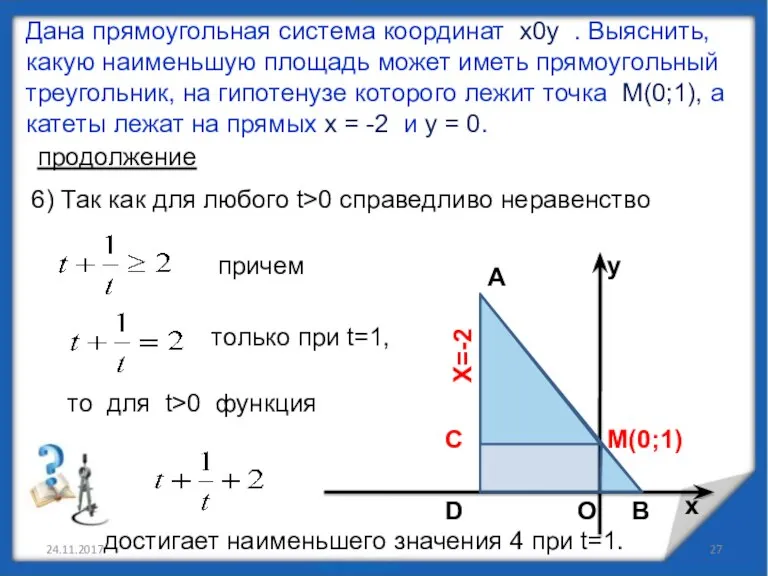
- 27. 24.11.2017 Дана прямоугольная система координат х0у . Выяснить, какую наименьшую площадь может иметь прямоугольный треугольник, на
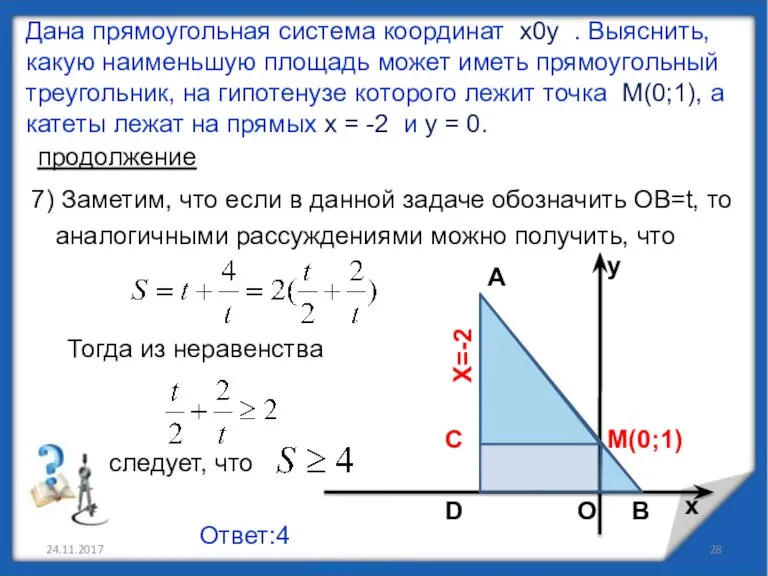
- 28. 24.11.2017 Дана прямоугольная система координат х0у . Выяснить, какую наименьшую площадь может иметь прямоугольный треугольник, на
- 29. 24.11.2017 Д/З: п.5.9 – выучить; выучить алгоритм решить №№5.94*, 5.95 + творческое задание (необязательное) Придумать прикладную
- 30. Продолжите фразы: Сегодня на уроке я узнал… Сегодня на уроке я научился… Сегодня на уроке я
- 32. Скачать презентацию


![24.11.2017 Функция f(x) задана на [a; b]. Определите max и min функции,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1143943/slide-11.jpg)












 Квадратный метр и квадратный сантиметр. 3 класс
Квадратный метр и квадратный сантиметр. 3 класс Формулы приведения
Формулы приведения Иррациональные неравенства. Неравенства с модулем
Иррациональные неравенства. Неравенства с модулем Function as one of the fundamental concepts at secondary school mathematics
Function as one of the fundamental concepts at secondary school mathematics Теория и практика статистических выводов. Лекция 3
Теория и практика статистических выводов. Лекция 3 Множество и его элементы
Множество и его элементы Центральные углы
Центральные углы Математические загадки
Математические загадки Интерактивная игра. Математический футбол
Интерактивная игра. Математический футбол Преобразование графика квадратичной функции
Преобразование графика квадратичной функции Презентация на тему ГИА 2013 Модуль «Геометрия» № 11
Презентация на тему ГИА 2013 Модуль «Геометрия» № 11  Производная и дифференциал функции
Производная и дифференциал функции Решение квадратных неравенств
Решение квадратных неравенств Презентация на тему Начертательная геометрия
Презентация на тему Начертательная геометрия  Самостоятельная работа к урокам 31-34
Самостоятельная работа к урокам 31-34 Квадратные уравнения. Задания
Квадратные уравнения. Задания Готовимся к новому учебному году. Повторяем математику
Готовимся к новому учебному году. Повторяем математику Обратные матрицы. Системы уравнений
Обратные матрицы. Системы уравнений Прогрессии
Прогрессии Работа с числами
Работа с числами Урок математики (2 класс)
Урок математики (2 класс) Алгоритмы. Понятие и свойства алгоритмов
Алгоритмы. Понятие и свойства алгоритмов Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Координатная плоскость
Координатная плоскость Параллельность прямых и плоскостей в пространстве с решением
Параллельность прямых и плоскостей в пространстве с решением Презентация на тему Полупрямая
Презентация на тему Полупрямая  Степени с рациональными показателями, их свойства
Степени с рациональными показателями, их свойства Преобразование иррациональных выражений
Преобразование иррациональных выражений