Слайд 2Цель работы:
Выяснить, каким способом можно составить алгоритмы для нахождения числа Пи с

помощью компьютера и узнать, какой способ поможет более точно вычислить это число.
Слайд 3Задачи работы
Ознакомиться с историей числа Пи
Найти необходимые формулы для вычисления числа Пи
Преобразовать

найденные формулы в алгоритмы в системе программирования PascalABC
Узнать, какой способ вычисления наиболее точный
Слайд 4Число Пи (греческая буква π) –
это математическая константа,
выражающая отношение длины
окружности

к длине её диаметра.
Число Пи иррационально и
бесконечно.
Слайд 5Формулы для нахождения числа пи
Ряд Мадхавы
Формула Джона Валлиса
Формула Вильгельма Лейбница
Формула Леонарда

Эйлера
Нахождение числа Пи с помощью рядов
Формула Джона Мэчина
Алгоритм Брента-Саламина
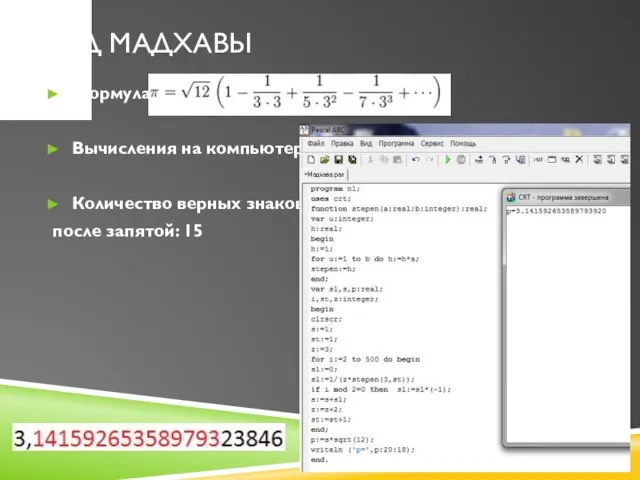
Слайд 6Ряд Мадхавы
Формула:
Вычисления на компьютере:
Количество верных знаков
после запятой: 15
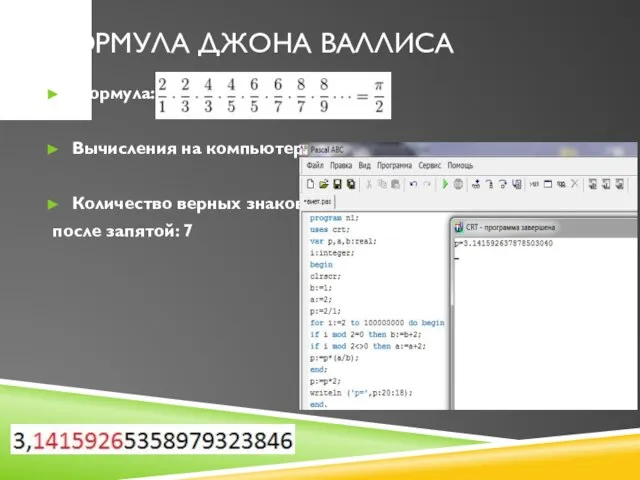
Слайд 7Формула Джона Валлиса
Формула:
Вычисления на компьютере:
Количество верных знаков
после запятой: 7
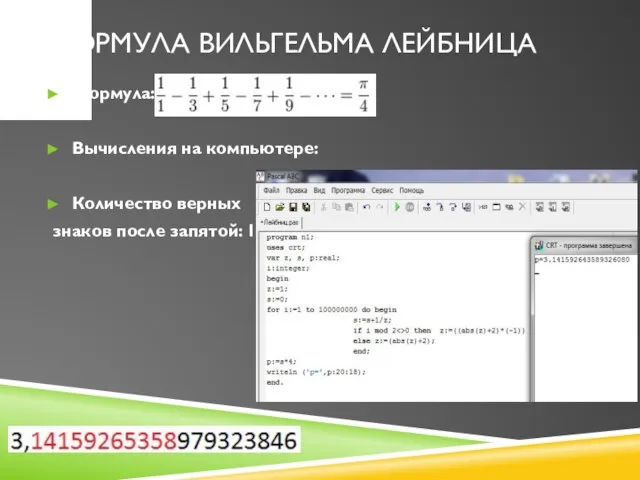
Слайд 8Формула Вильгельма Лейбница
Формула:
Вычисления на компьютере:
Количество верных
знаков после запятой: 11
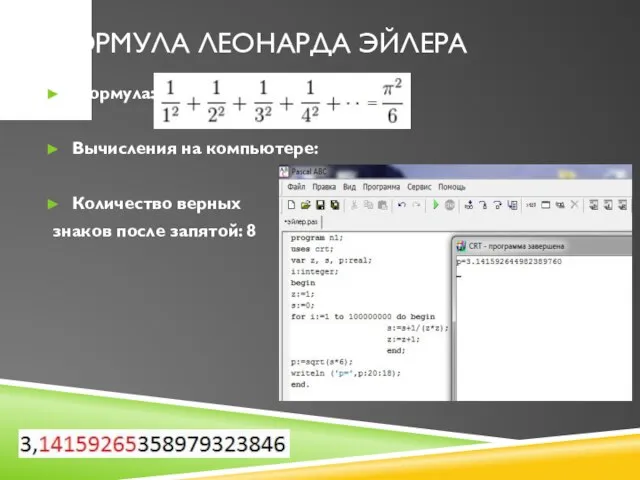
Слайд 9Формула Леонарда Эйлера
Формула:
Вычисления на компьютере:
Количество верных
знаков после запятой: 8
Слайд 10Нахождение числа Пи с помощью рядов
Формула:
Вычисления на компьютере:
Количество верных
знаков после запятой: 7
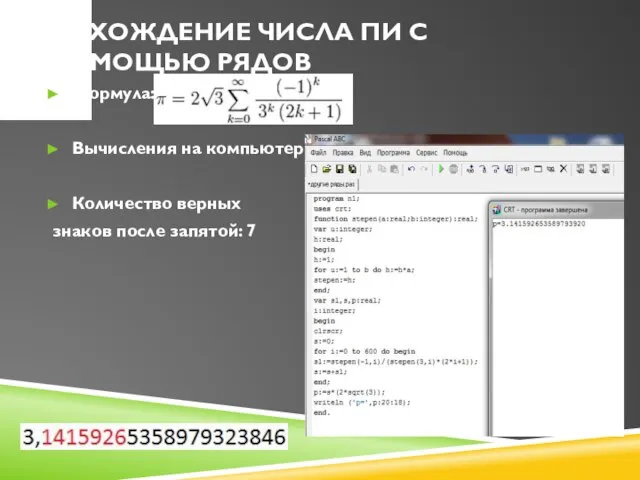
Слайд 11Нахождение числа Пи с помощью рядов
Формула:
Вычисления на компьютере:
Количество верных
знаков после запятой:
4
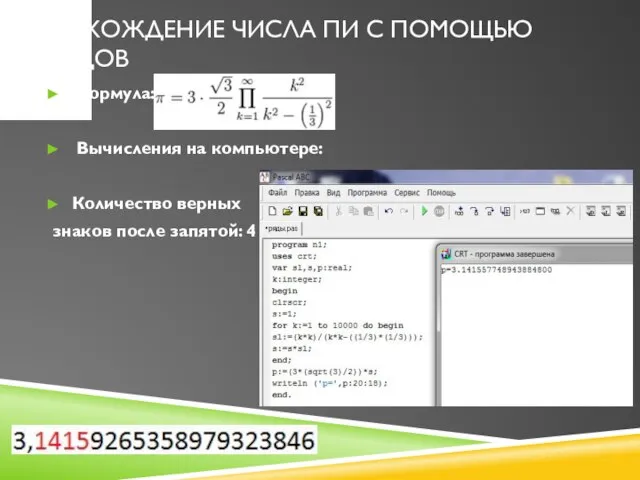
Слайд 12Нахождение числа Пи с помощью рядов
Формула:
Вычисления на компьютере:
Количество верных
знаков после запятой: 3
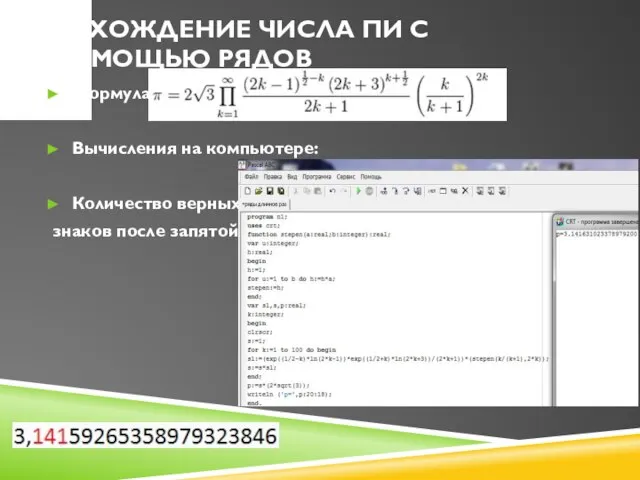
Слайд 13Формула Джона Мэчина
Формула:
Вычисления на компьютере:
Количество верных
знаков после запятой: 1
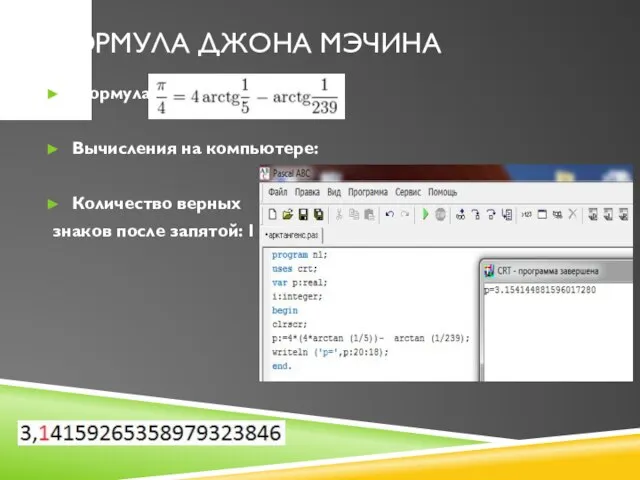
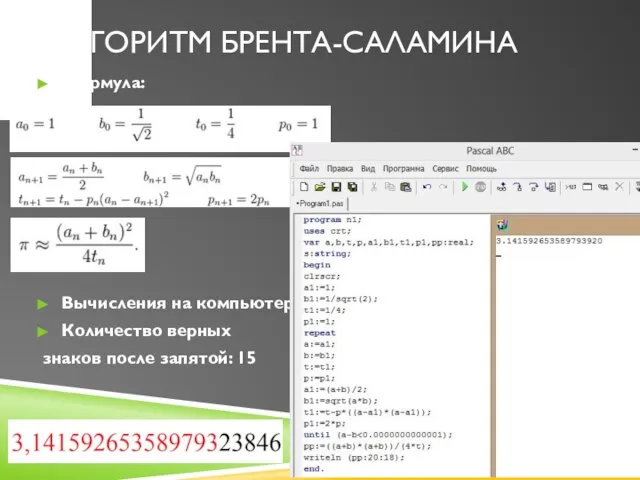
Слайд 14Алгоритм Брента-Саламина
Формула:
Вычисления на компьютере:
Количество верных
знаков после запятой: 15
Слайд 15Вывод
Проанализировав решенные мною задачи, я выяснила, что наиболее точными способами нахождения числа

Пи на компьютере являются:
Ряд Мадхавы (15 знаков)
Формула Лейбница (11 знаков)
Алгоритм Брента-Саламина (15 знаков)
Классические системы программирования, к которым
относится Pascal, не пригодны для вычислений больших и
очень маленьких чисел, поэтому, в приведенных мною
примерах, я не достигла точности, описанной в
литературе.














 «Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами»
«Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами» Роспись петуха по мотивам Филимоновской росписи
Роспись петуха по мотивам Филимоновской росписи Гражданское право. Понятие и виды сроков в гражданском праве
Гражданское право. Понятие и виды сроков в гражданском праве Модернизм
Модернизм Какие фигуры изображены на рисунке ?
Какие фигуры изображены на рисунке ? Перенос слова переносятся по слогам
Перенос слова переносятся по слогам Принтеры
Принтеры Методическая разработка «Создание презентаций» Элективный курс для 10 класса.
Методическая разработка «Создание презентаций» Элективный курс для 10 класса. Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне
Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне Федеральное Собрание РФ
Федеральное Собрание РФ Инжиниринг нефтехимии и нефтегазопереработки
Инжиниринг нефтехимии и нефтегазопереработки Китайский клуб МИИТа
Китайский клуб МИИТа Мой город, с тебя начинается Родина (город Сатка)
Мой город, с тебя начинается Родина (город Сатка) Спартакиада пенсионеров муниципального образования Город Гатчина
Спартакиада пенсионеров муниципального образования Город Гатчина Эры. Основные события органического мира
Эры. Основные события органического мира Презентация на тему Операционные системы на мобильных устройствах
Презентация на тему Операционные системы на мобильных устройствах  Живопись
Живопись Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы
Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70
Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70 МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942)
МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942) Векторы в пространстве и не только
Векторы в пространстве и не только Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники Трансформация изображения через трансформацию формы - серия открыток
Трансформация изображения через трансформацию формы - серия открыток ОРНАМЕНТЫ в национальном костюме
ОРНАМЕНТЫ в национальном костюме Цветник для солнечного места “Степной бриз ”
Цветник для солнечного места “Степной бриз ” Презентация на тему Тургенев. Стихи в прозе
Презентация на тему Тургенев. Стихи в прозе 287 Воскресшему служу я
287 Воскресшему служу я Берлину заменить Северный поток-2 другим проектом
Берлину заменить Северный поток-2 другим проектом