Элементы теории графов. Способы обходов графов

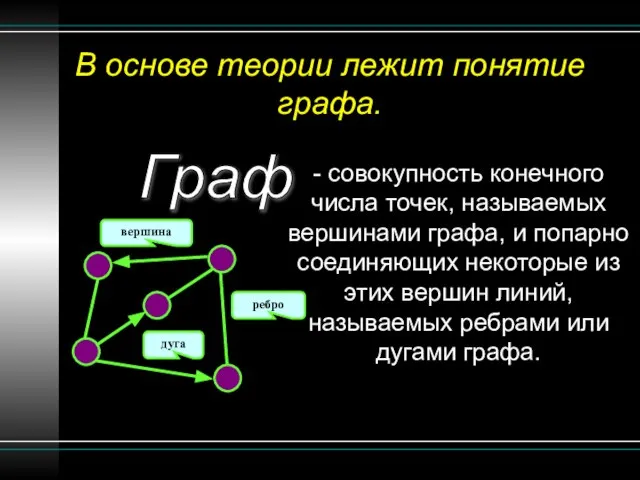
В основе теории лежит понятие графа.
- совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из этих вершин линий, называемых ребрами или дугами графа.
Граф

Первая работа по теории графов, принадлежащая известному швейцарскому математику Л. Эйлеру, появилась в 1736 г., связанная с решением известной головоломки о мостах Кёнигсберга. Толчок к развитию теория графов получила на рубеже ХIX и ХХ столетий, когда резко возросло число работ в области топологии и комбинаторики.

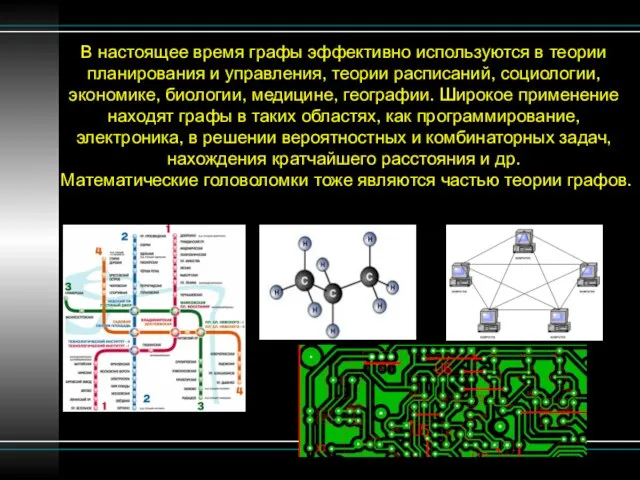
В настоящее время графы эффективно используются в теории планирования и управления, теории расписаний, социологии, экономике, биологии, медицине, географии. Широкое применение находят графы в таких областях, как программирование, электроника, в решении вероятностных и комбинаторных задач, нахождения кратчайшего расстояния и др.
Математические головоломки тоже являются частью теории графов.

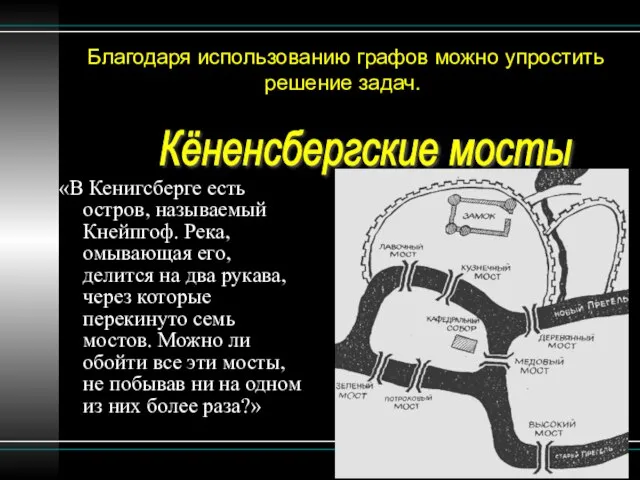
Благодаря использованию графов можно упростить решение задач.
«В Кенигсберге есть остров, называемый Кнейпгоф. Река, омывающая его, делится на два рукава, через которые перекинуто семь мостов. Можно ли обойти все эти мосты, не побывав ни на одном из них более раза?»
Кёненсбергские мосты

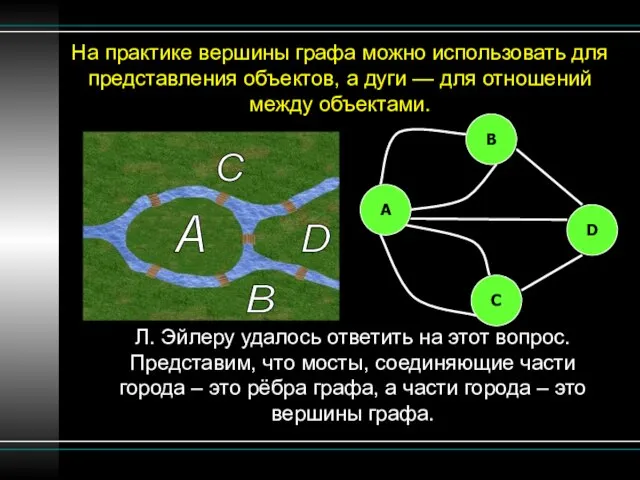
На практике вершины графа можно использовать для представления объектов, а дуги — для отношений между объектами.
Л. Эйлеру удалось ответить на этот вопрос.
Представим, что мосты, соединяющие части города – это рёбра графа, а части города – это вершины графа.
A
A
C
B
D

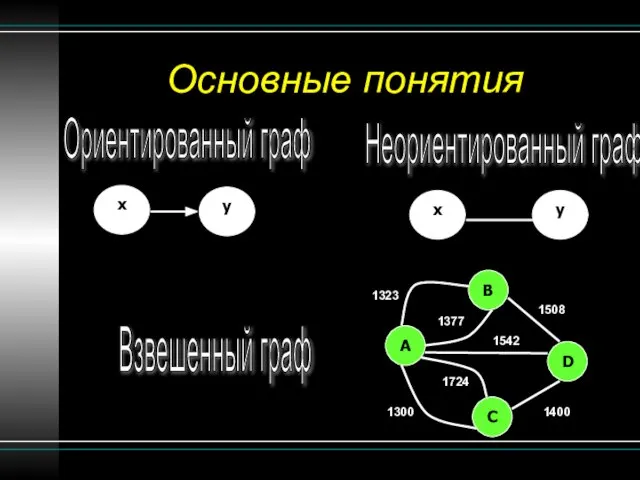
Основные понятия
Ориентированный граф
Неориентированный граф
x
y
x
y
Взвешенный граф

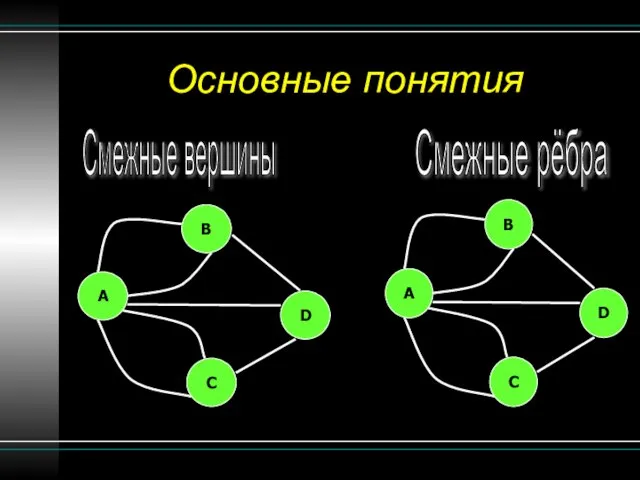
Основные понятия
Смежные вершины
Смежные рёбра
B
A
C
D
B
A
C
D

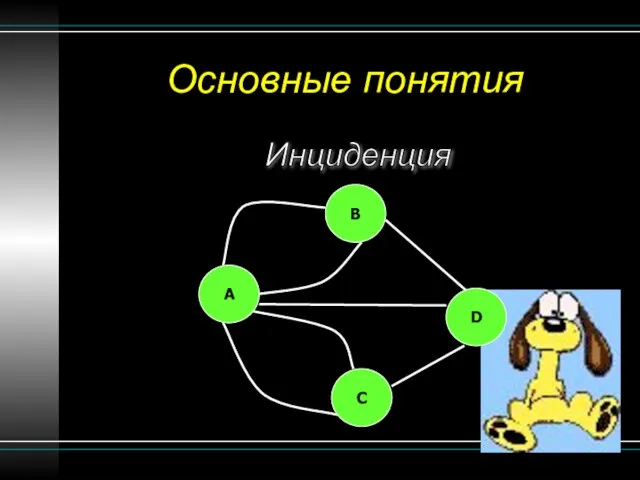
Основные понятия
Инциденция
B
A
C
D

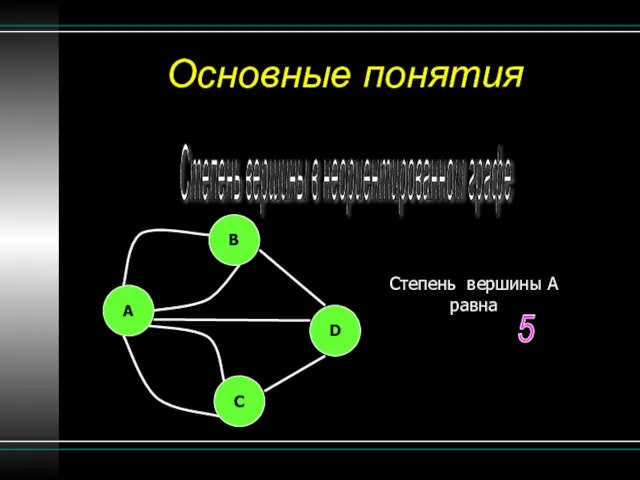
Основные понятия
Степень вершины в неориентированном графе
Степень вершины A равна
B
A
C
D
5

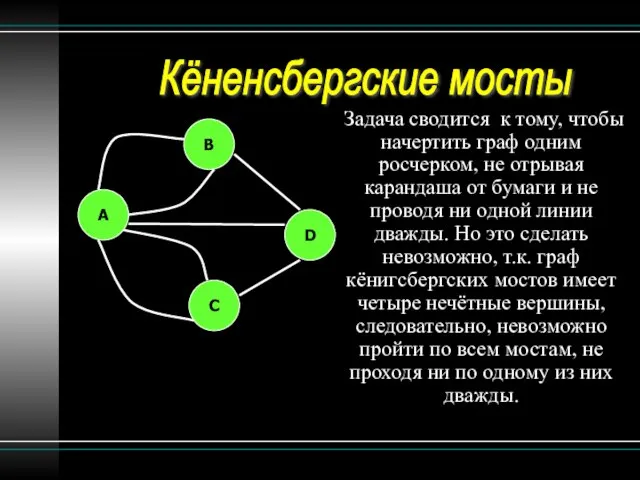
Задача сводится к тому, чтобы начертить граф одним росчерком, не отрывая карандашa от бумаги и не проводя ни одной линии дважды. Но это сделать невозможно, т.к. граф кёнигсбергских мостов имеет четыре нечётные вершины, следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Кёненсбергские мосты
B
A
C
D

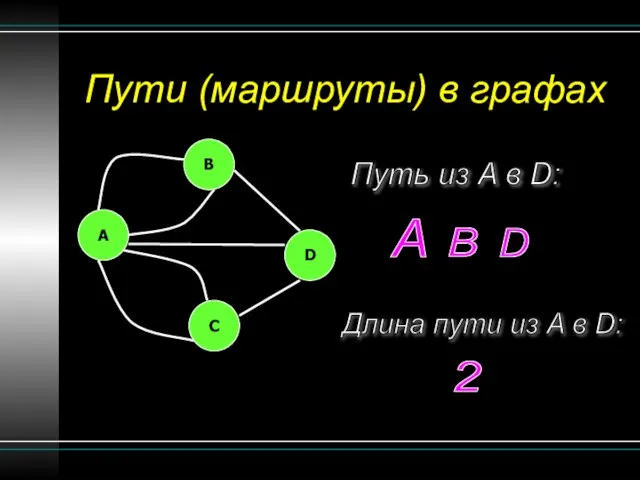
Пути (маршруты) в графах
Путь из A в D:
Длина пути из A в D:
B
A
C
D
A
B
D
2

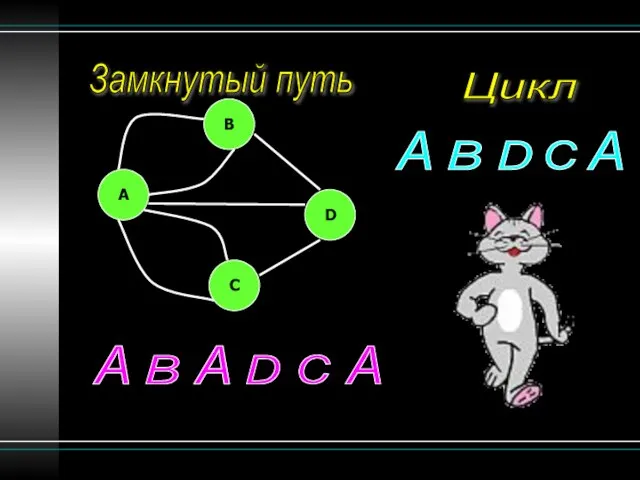
Замкнутый путь
Цикл
B
A
C
D
A
B
A
D
C
A
A
A
A
B
D
C
A

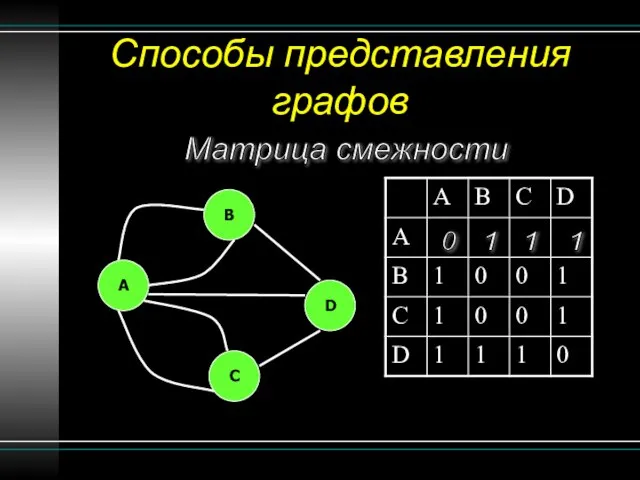
Способы представления графов
Матрица смежности
B
A
C
D
0
1
1
1

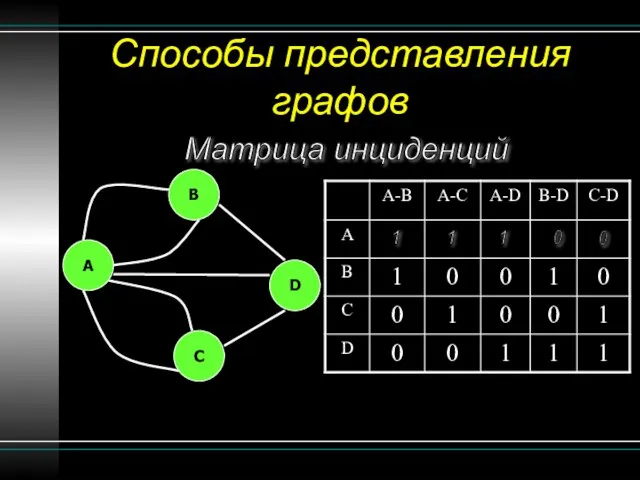
Способы представления графов
Матрица инциденций
1
B
A
C
D
1
1
0
0

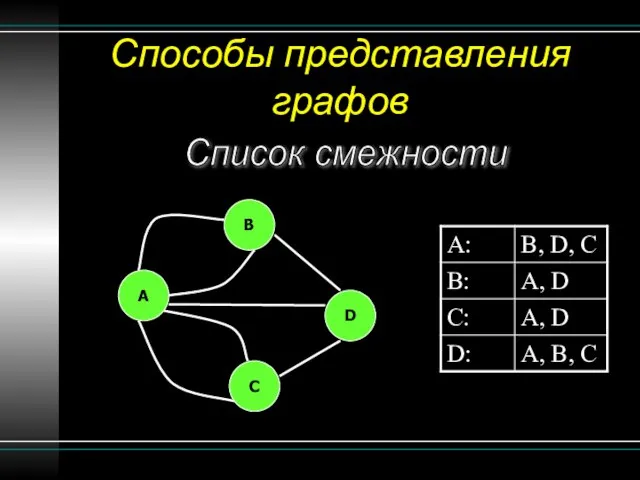
Способы представления графов
Список смежности

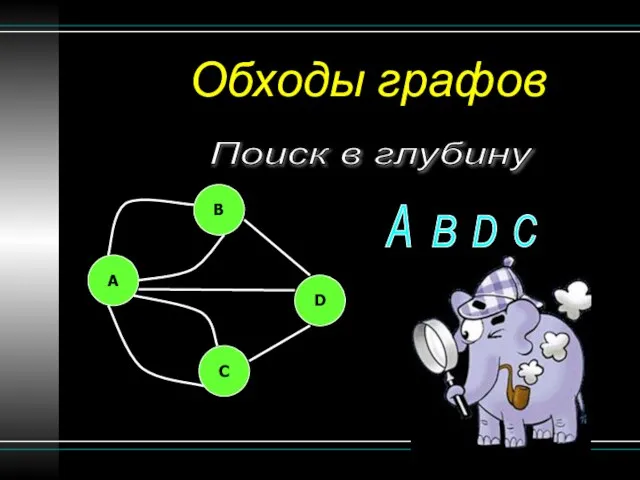
Обходы графов
Поиск в глубину
B
A
C
D
A
B
D
C

Program graf;
Var n,v,u: integer;
gr: array [1..30, 1..30] of integer;
nov: array [1..15] of boolean;
procedure dfs (v: integer);
var u: integer;
Begin
Readln;
Write (v,’ ’);
nov [v]:=false;
For u:=1 to n do
If (gr[v,u]=1) and (nov[u]) then dfs (u);
End;
Begin
n:=4;
for v:=1 to n do
begin
nov [v]:= true;
Writeln;
For u:=1 to n do begin nov [u]:=true;
Write (‘ gr [‘ ,v,u, ‘ ]=‘);
Read (gr [v,u]);
Размерность массива
n =4
End;
End;
For v:=1 to n do begin
IF nov [v] then dfs (v);
End;
Readln;
End.

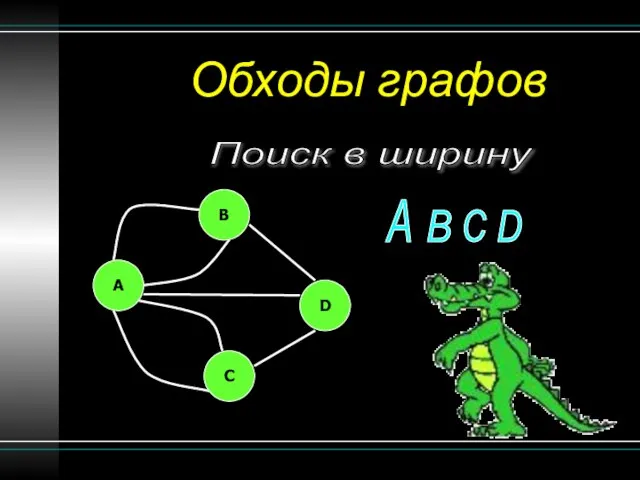
Обходы графов
Поиск в ширину
B
A
C
D
A
B
C
D