favorskiIVM

Основные направления математического моделирования гемодинамики
Моделирование течения крови в отдельном сосуде
2D и 3D модели течения в крупных сосудах (уравнения Навье-Стокса)
(моделирование упругости стенки сосуда, турбулентность течения, многокомпонентность крови (не ньютоновская жидкость), взаимодействие со стенками сосуда, области бифуркации сосудов, моделирование тромбообразования, стенозов, аневризмов и т.д.)
2D и 3D модели течения крови в мелких сосудах (капиллярах)с учетом реологии.
Моделирование течения крови в сердце (2D и 3D модели)
Моделирование течения крови в сети сосудов (дерево сосудов, замкнутая система) для исследования общих закономерностей течения крови.
- На основе балансных соотношений
- На аналогиях с «электрической цепью»
Квазиодномерное приближение:
- соответствует типу сосудистой сети
- дает возможность описать систему кровообращения в целом
позволяет отслеживать параметры течения крови вдоль сосуда
- позволяет учесть особенности каждого сосуда
- является основой для построения разномасштабных моделей
-предоставляет возможность расчета переноса веществ кровью
-предоставляет возможность использовать различные модели сосудов и органов
-использует доступные физиологические данные
-обладает хорошей точностью
-предъявляет разумные требования к вычислительным мощностям

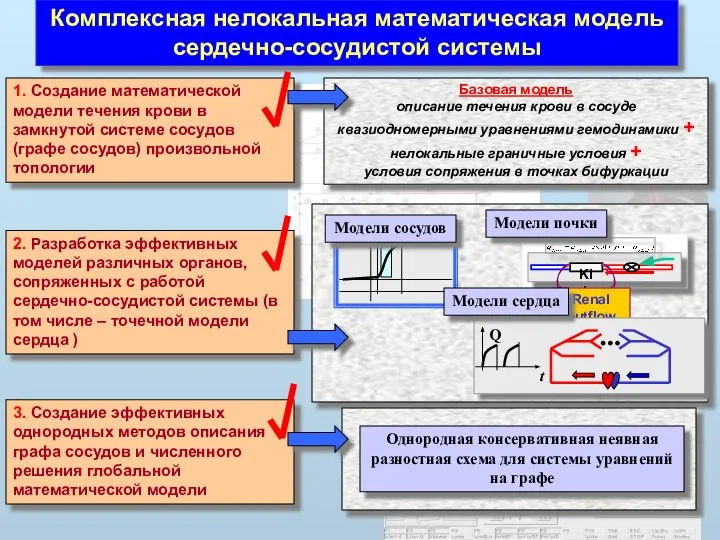
Комплексная нелокальная математическая модель сердечно-сосудистой системы
Базовая модель
описание течения крови в сосуде квазиодномерными уравнениями гемодинамики + нелокальные граничные условия +
условия сопряжения в точках бифуркации
1. Создание математической модели течения крови в замкнутой системе сосудов (графе сосудов) произвольной топологии
2. Разработка эффективных моделей различных органов, сопряженных с работой сердечно-сосудистой системы (в том числе – точечной модели сердца )
3. Создание эффективных однородных методов описания графа сосудов и численного решения глобальной математической модели
Модели сосудов
Модели почки
Модели сердца
Однородная консервативная неявная разностная схема для системы уравнений на графе

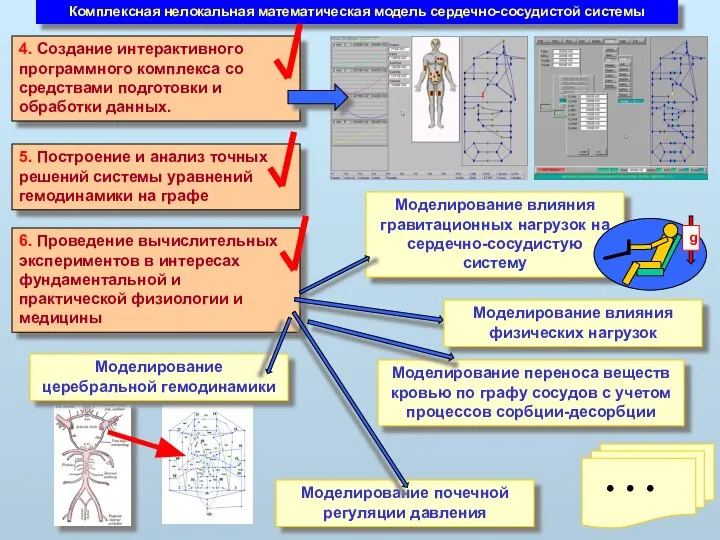
Комплексная нелокальная математическая модель сердечно-сосудистой системы
6. Проведение вычислительных экспериментов в интересах фундаментальной и практической физиологии и медицины
5. Построение и анализ точных решений системы уравнений гемодинамики на графе
4. Создание интерактивного программного комплекса со средствами подготовки и обработки данных.
Моделирование церебральной гемодинамики
Моделирование влияния гравитационных нагрузок на сердечно-сосудистую систему
Моделирование почечной регуляции давления
Моделирование влияния физических нагрузок
. . .
Моделирование переноса веществ кровью по графу сосудов с учетом процессов сорбции-десорбции

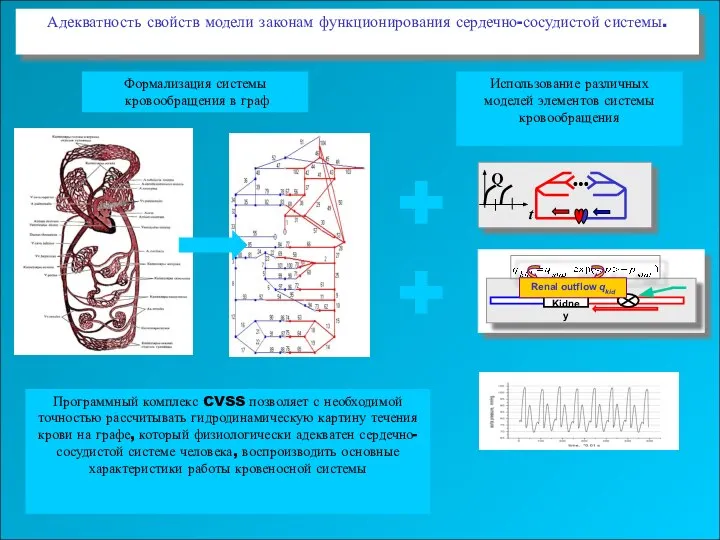
Адекватность свойств модели законам функционирования сердечно-сосудистой системы.
+
+
Renal outflow qkid
Программный комплекс CVSS позволяет с необходимой точностью рассчитывать гидродинамическую картину течения крови на графе, который физиологически адекватен сердечно-сосудистой системе человека, воспроизводить основные характеристики работы кровеносной системы
Формализация системы
кровообращения в граф
Использование различных моделей элементов системы кровообращения

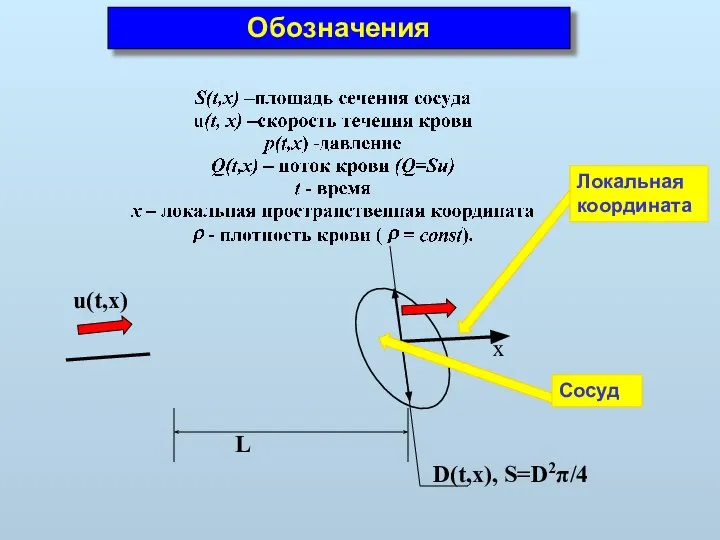
Обозначения
x
u(t,x)
L
D(t,x), S=D2π/4
Сосуд
Локальная координата

x- координата вдоль оси сосуда, t - время, S(x,t) - площадь сечения сосуда, u(x,t) - скорость движения крови (направлена вдоль оси сосуда), p(x,t) - давление в крови, ρ=const - плотность крови, L- длина сосуда, F(x,t) объемная плотность силы.
Одиночный сосуд рассматриваем как трубку кругового сечения, протяженную по сравнению со своими поперечными размерами. Под эластичностью стенок понимается возможность изменения сечения сосуда под действием давления.
В основу описания движения крови в сосуде положены законы сохранения массы и импульса (количества движения).
Интегральный вид уравнений
S=S(p) – Эмпирическая зависимость площади сечения сосуда от давления.
Система уравнений гемодинамики в квизиодномерном приближении
Модель гемодинамики в одном сосуде

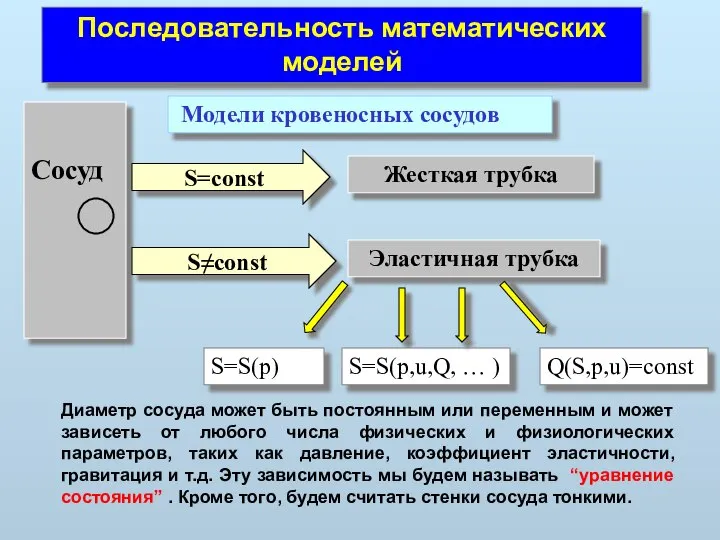
Последовательность математических моделей
Модели кровеносных сосудов
Сосуд
Жесткая трубка
Эластичная трубка
S=const
S≠const
S=S(p)
S=S(p,u,Q, … )
Диаметр сосуда может быть постоянным или переменным и может зависеть от любого числа физических и физиологических параметров, таких как давление, коэффициент эластичности, гравитация и т.д. Эту зависимость мы будем называть “уравнение состояния” . Кроме того, будем считать стенки сосуда тонкими.
Q(S,p,u)=const

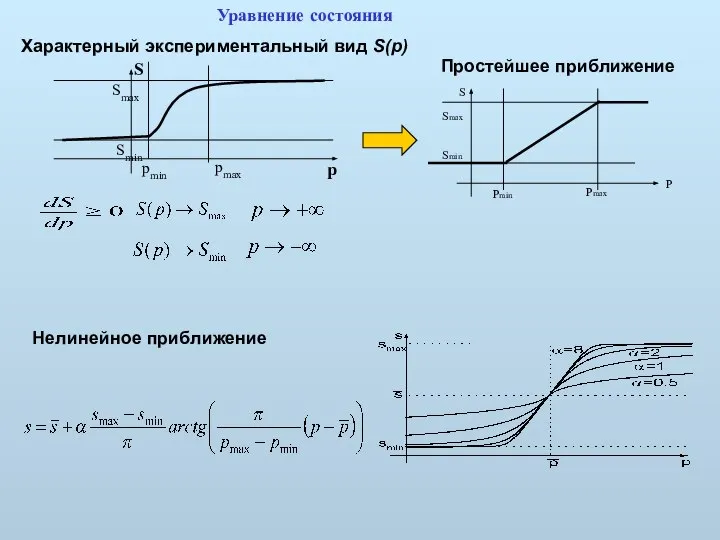
Характерный экспериментальный вид S(p)
Простейшее приближение
Нелинейное приближение
Уравнение состояния

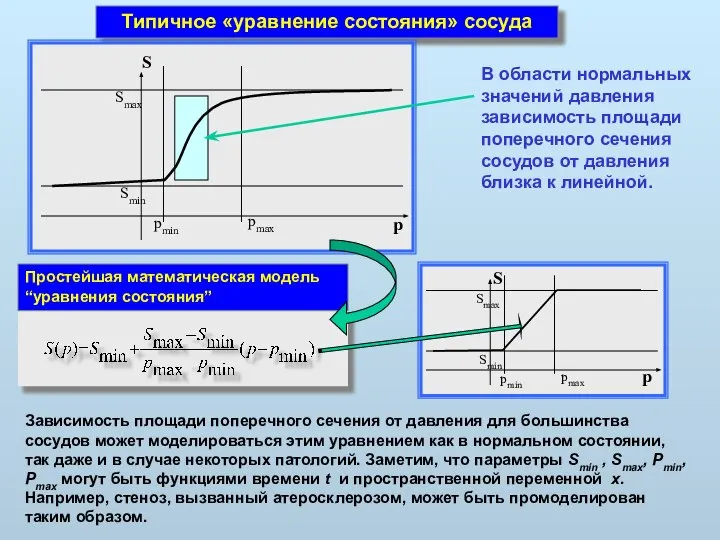
Типичное «уравнение состояния» сосуда
В области нормальных значений давления зависимость площади поперечного сечения сосудов от давления близка к линейной.
Простейшая математическая модель “уравнения состояния”
Зависимость площади поперечного сечения от давления для большинства сосудов может моделироваться этим уравнением как в нормальном состоянии, так даже и в случае некоторых патологий. Заметим, что параметры Smin , Smax, Pmin, Pmax могут быть функциями времени t и пространственной переменной x. Например, стеноз, вызванный атеросклерозом, может быть промоделирован таким образом.

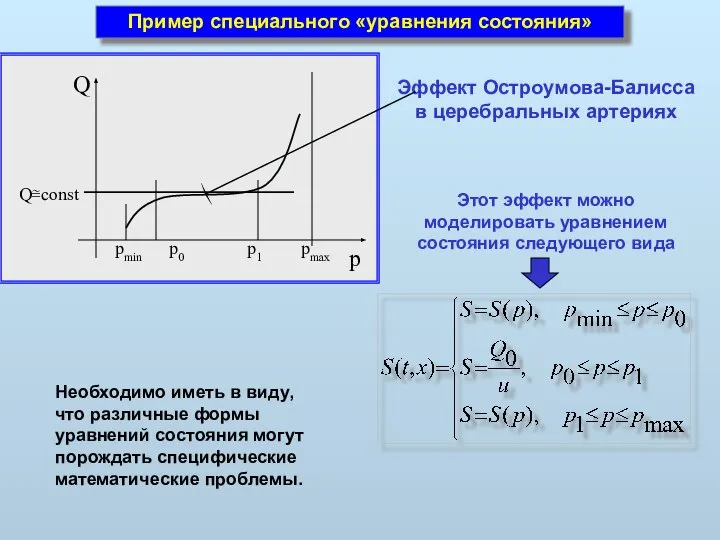
Пример специального «уравнения состояния»
p0
Эффект Остроумова-Балисса в церебральных артериях
Этот эффект можно моделировать уравнением состояния следующего вида
Необходимо иметь в виду, что различные формы уравнений состояния могут порождать специфические математические проблемы.

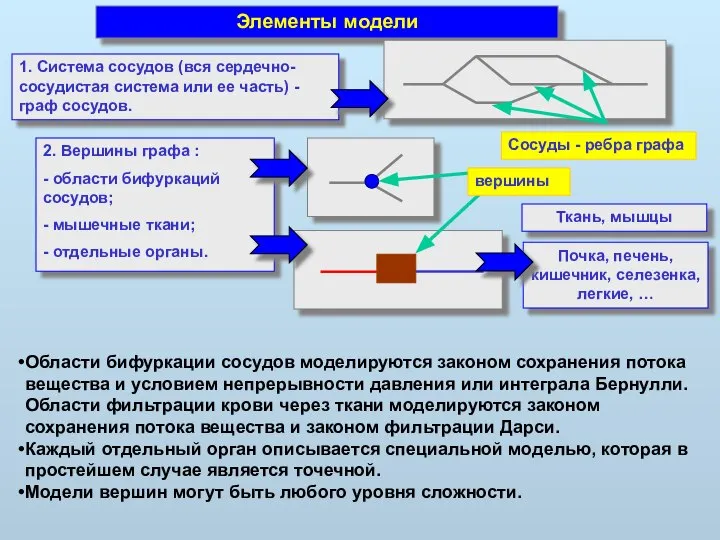
Сосуды - ребра графа
Элементы модели
1. Система сосудов (вся сердечно-сосудистая система или ее часть) - граф сосудов.
2. Вершины графа :
- области бифуркаций сосудов;
- мышечные ткани;
- отдельные органы.
вершины
Области бифуркации сосудов моделируются законом сохранения потока вещества и условием непрерывности давления или интеграла Бернулли. Области фильтрации крови через ткани моделируются законом сохранения потока вещества и законом фильтрации Дарси.
Каждый отдельный орган описывается специальной моделью, которая в простейшем случае является точечной.
Модели вершин могут быть любого уровня сложности.

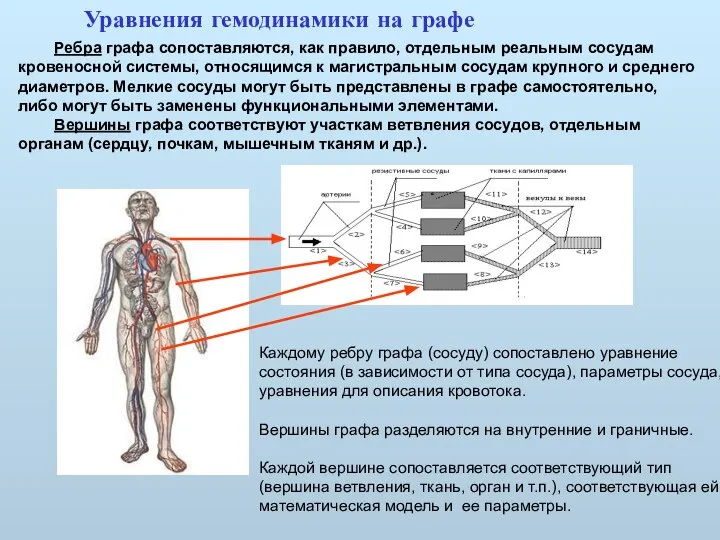
Ребра графа сопоставляются, как правило, отдельным реальным сосудам кровеносной системы, относящимся к магистральным сосудам крупного и среднего диаметров. Мелкие сосуды могут быть представлены в графе самостоятельно, либо могут быть заменены функциональными элементами.
Вершины графа соответствуют участкам ветвления сосудов, отдельным органам (сердцу, почкам, мышечным тканям и др.).
Уравнения гемодинамики на графе
Каждому ребру графа (сосуду) сопоставлено уравнение состояния (в зависимости от типа сосуда), параметры сосуда, уравнения для описания кровотока.
Вершины графа разделяются на внутренние и граничные.
Каждой вершине сопоставляется соответствующий тип (вершина ветвления, ткань, орган и т.п.), соответствующая ей математическая модель и ее параметры.

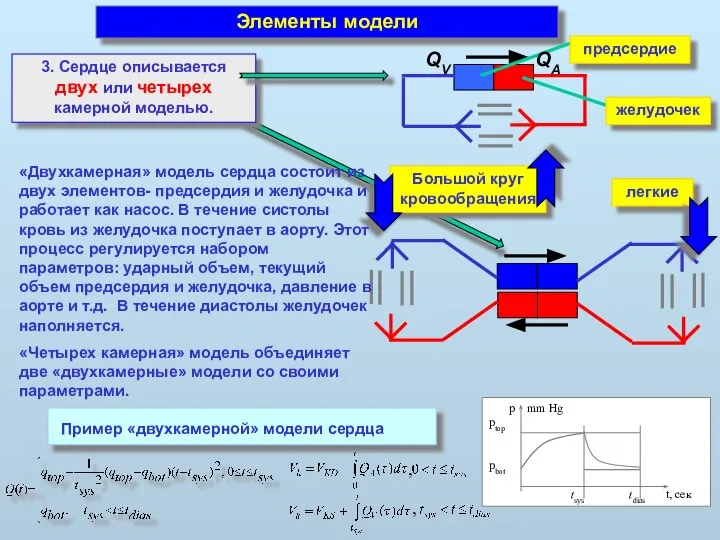
Элементы модели
3. Сердце описывается двух или четырех
камерной моделью.
легкие
Большой круг кровообращения
желудочек
предсердие
«Двухкамерная» модель сердца состоит из двух элементов- предсердия и желудочка и работает как насос. В течение систолы кровь из желудочка поступает в аорту. Этот процесс регулируется набором параметров: ударный объем, текущий объем предсердия и желудочка, давление в аорте и т.д. В течение диастолы желудочек наполняется.
«Четырех камерная» модель объединяет две «двухкамерные» модели со своими параметрами.
Пример «двухкамерной» модели сердца
QV
QA
,
,

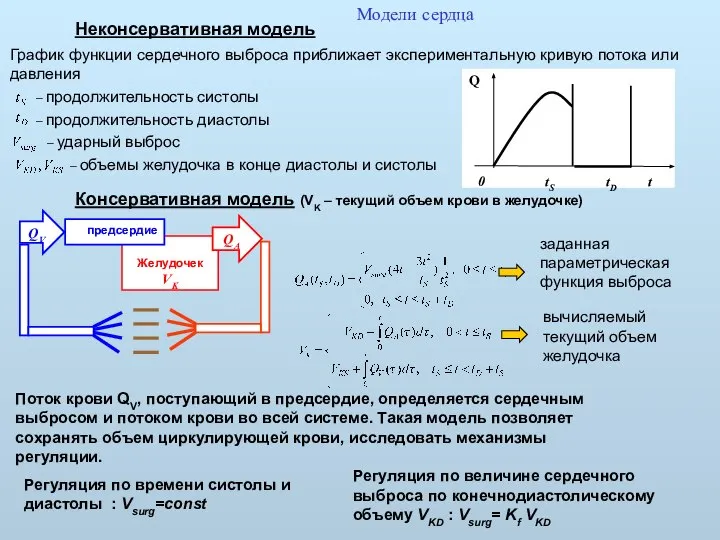
Модели сердца
Неконсервативная модель
График функции сердечного выброса приближает экспериментальную кривую потока или давления
– продолжительность систолы
– продолжительность диастолы
Консервативная модель (VK – текущий объем крови в желудочке)
Желудочек
VK
QA
предсердие
QV
Регуляция по величине сердечного выброса по конечнодиастолическому объему VKD : Vsurg= Kf VKD
Регуляция по времени систолы и диастолы : Vsurg=const
– ударный выброс
– объемы желудочка в конце диастолы и систолы
заданная параметрическая функция выброса
вычисляемый текущий объем желудочка
Поток крови QV, поступающий в предсердие, определяется сердечным выбросом и потоком крови во всей системе. Такая модель позволяет сохранять объем циркулирующей крови, исследовать механизмы регуляции.

Математическая модель на графе
ОБОЗНАЧЕНИЯ
S(t,x) –площадь поперечного сечения
u(t, x) -скорость потока крови
p(t,x) -давление
t - время
x - локальная пространственная координата
ρ - плотность крови ( ρ = const).
FT – сила трения
FT – сила тяжести
2. Каждой вершине графа, соответствующей области бифуркации сосудов, сопоставлено уравнение неразрывности и условие непрерывности интеграла Бернулли.
3. Каждой вершине графа, соответствующей тканям, сопоставлено уравнение сохранения вещества и уравнение фильтрации Дарси.
1. Каждому ребру графа сопоставлена система уравнений гемодинамики

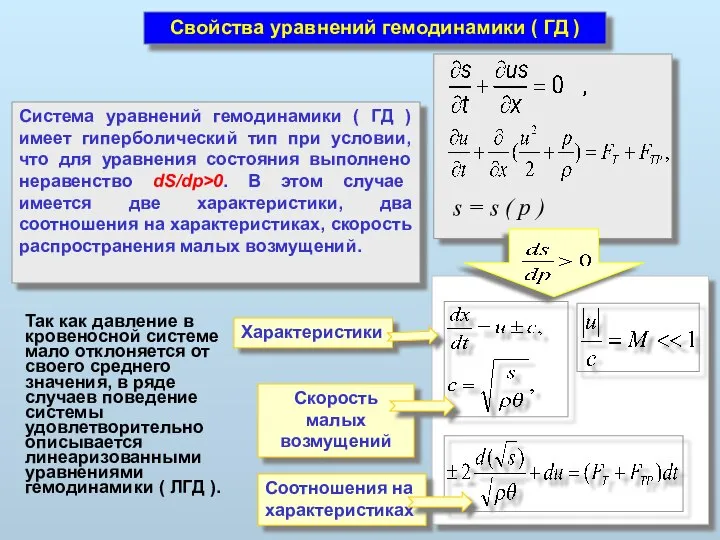
Свойства уравнений гемодинамики ( ГД )
Система уравнений гемодинамики ( ГД ) имеет гиперболический тип при условии, что для уравнения состояния выполнено неравенство dS/dp>0. В этом случае имеется две характеристики, два соотношения на характеристиках, скорость распространения малых возмущений.
Соотношения на характеристиках
Характеристики
Скорость малых возмущений
Так как давление в кровеносной системе мало отклоняется от своего среднего значения, в ряде случаев поведение системы удовлетворительно описывается линеаризованными уравнениями гемодинамики ( ЛГД ).

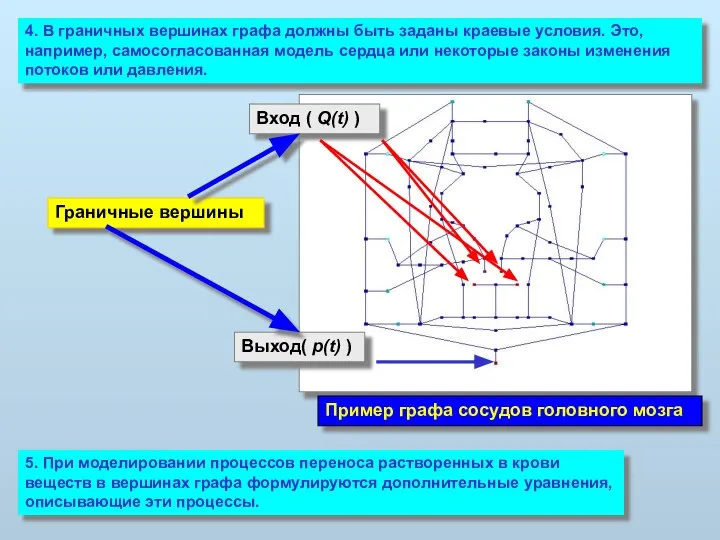
4. В граничных вершинах графа должны быть заданы краевые условия. Это, например, самосогласованная модель сердца или некоторые законы изменения потоков или давления.
Граничные вершины
Вход ( Q(t) )
Выход( p(t) )
Пример графа сосудов головного мозга
5. При моделировании процессов переноса растворенных в крови веществ в вершинах графа формулируются дополнительные уравнения, описывающие эти процессы.

Перенос вещества с массовой концентрацией C с учетом диффузии (D=const- коэффициент диффузии) по сосуду с переменным сечением описывается дифференциальным уравнением
число Маха М<<1 , сечение сосудов ограничено снизу
Уравнения переноса вещества для графа
Сl,k – концентрация l-ого вещества в k –ом сосуде, f – источник , ϕ - химические реакции.
В вершинах ветвления - закон Киргхофа с учетом диффузии и равенство соответствующих концентраций.
Здесь t – время начала диастолы, а Δt изменяется от нуля до величины равной продолжительности диастолы. Индекс a обозначает аорту. Аналогичное выражение выписывается для концентраций во время систолы.
Уравнения для концентраций в сердце
Рассматривается случай полного перемешивания веществ Cl в желудочке. Позволяют рассматривать замкнутую систему кровообращения с сохранением количества веществ во всей системе.
Перенос веществ по графу сосудов

Уравнения гемодинамики на ребре i
Уравнения сопряжения и граничные условия
Неявная разностная схема
, i=1,2,3,4 - весовые коэффициенты
(на каждом ребре)
Неявная аппроксимация уравнений сопряжения и граничных условий
aS ,au – коэффициенты искусственной вязкости
λi , βI – коэффициенты искусственной дисперсии, например β2 =
Численный алгоритм и программный комплекс
Разностная схема апробирована на точных аналитических решениях

Линеаризация по Ньютону
Линеаризованное разностное уравнение неразрывности в каждом внутреннем узле j дискретной сетки на каждом ребре графа
Линеаризованное разностное уравнение движения

задавать граф сосудов произвольной сложности;
задавать параметры сосудов графа, как по отдельности, так и групповым образом;
выбирать модели для описания сосудов и органов и задавать их параметры;
выбирать метод расчета и его параметры;
осуществлять контроль за корректностью и непротиворечивостью задания начальных данных, как физиологических, так и вычислительных;
отображать в ходе расчета необходимую информацию в численном или графическом виде, как локальную в любой точке рассматриваемого графа так и интегральную и записывать численные данные для дальнейшей обработки;
в режиме текущего расчета изменять топологию графа, параметры моделей и алгоритма;
обрабатывать результаты численного расчета после окончания или прерывания данной сессии моделирования;
реализовать расширяемость комплекса за счет включения новых моделей и процессов.
Разработан программный комплекс, который позволяет:

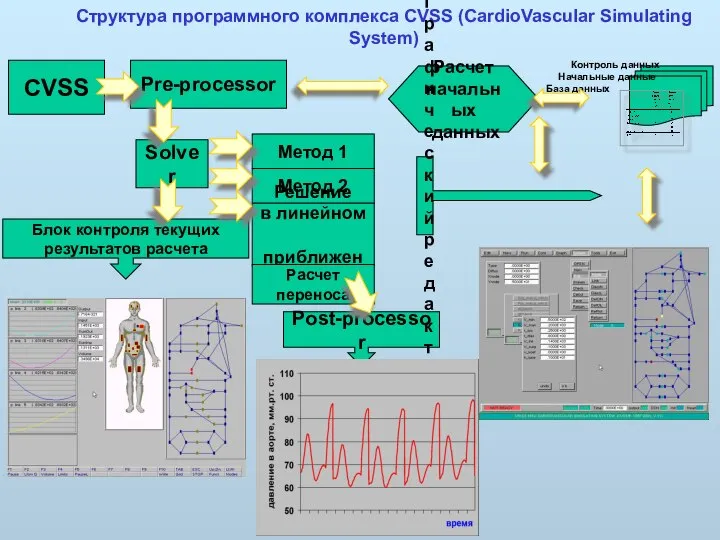
Структура программного комплекса CVSS (CardioVascular Simulating System)
CVSS
Pre-processor
Расчет
начальных
данных
Блок контроля текущих
результатов расчета
Post-processor
Solver
Графический
редактор
Расчет
переноса

Численные методы и алгоритмы
3. Разработана упрощенная конечно - разностная схема для решения уравнений гемодинамики.
1. Разработан специальный формат описания произвольного графа сосудов.
4. Полная нелинейная система разностных уравнений решается с использованием итерационных методов (метод Ньютона).
5. Линеаризованная система разностных уравнений решается с использованием прямых методов.
2. На каждом ребре графа использована однородная консервативная разностная схема второго порядка аппроксимации.

Эволюция малых возмущений средних стационарных значений скорости и давления в потоке крови описывается на каждом ребре графа сосудистой системы линеаризованными уравнениями гемодинамики:
Эта система уравнений замыкается линеаризованными условиями сопряжения во внутренних вершинах графа:
и линеаризованными краевыми условиями в граничных вершинах графа.
Линейное приближение для уравнений гемодинамики (ЛГД)

Общее решение ЛГД уравнений на любом i-ом ребре графа представляет собой суперпозицию двух произвольных волн, распространяющихся в противоположных направлениях (|u|<с):
Волны скорости и давления, проходя через вершины графа, меняют
величину своих амплитуд и фазу

Коэффициент прохождения волны скорости через вершину графа из ребра j в ребро i
Бегущие волны определяются следующей формулой:
Коэффициент отражения волны скорости от вершины графа на ребре i
j
i
i

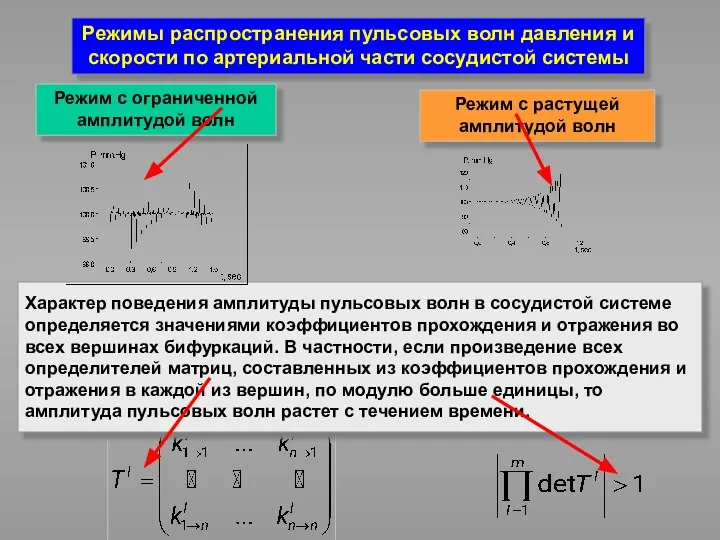
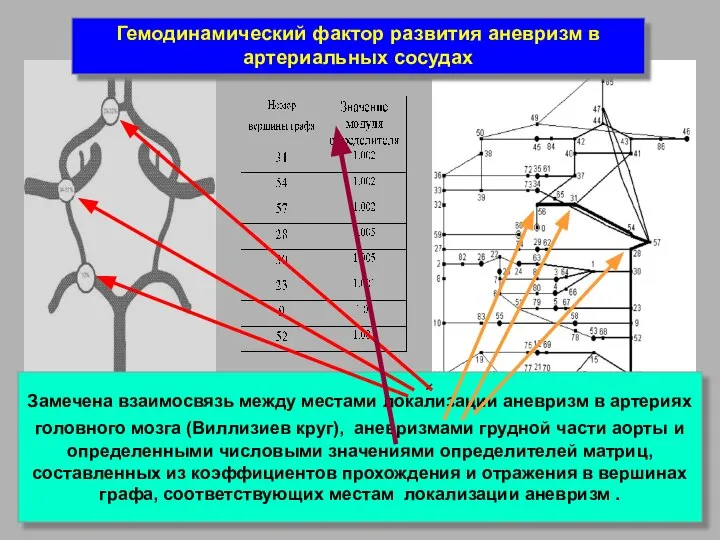
Характер поведения амплитуды пульсовых волн в сосудистой системе
определяется значениями коэффициентов прохождения и отражения во
всех вершинах бифуркаций. В частности, если произведение всех
определителей матриц, составленных из коэффициентов прохождения и
отражения в каждой из вершин, по модулю больше единицы, то
амплитуда пульсовых волн растет с течением времени.
Режим с растущей амплитудой волн
Режимы распространения пульсовых волн давления и скорости по артериальной части сосудистой системы
Режим с ограниченной амплитудой волн

Замечена взаимосвязь между местами локализации аневризм в артериях
головного мозга (Виллизиев круг), аневризмами грудной части аорты и
определенными числовыми значениями определителей матриц,
составленных из коэффициентов прохождения и отражения в вершинах
графа, соответствующих местам локализации аневризм .
Гемодинамический фактор развития аневризм в артериальных сосудах

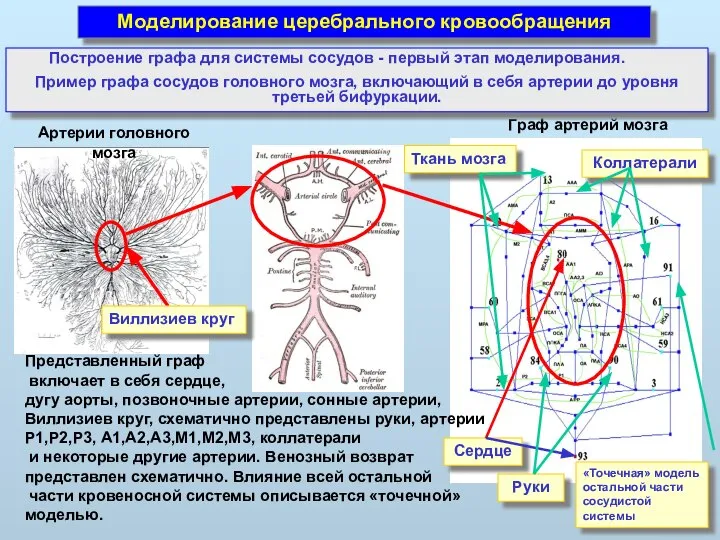
Моделирование церебрального кровообращения
Построение графа для системы сосудов - первый этап моделирования.
Пример графа сосудов головного мозга, включающий в себя артерии до уровня третьей бифуркации.
Ткань мозга
Коллатерали
Сердце
Руки
«Точечная» модель остальной части сосудистой системы
Виллизиев круг
Представленный граф
включает в себя сердце,
дугу аорты, позвоночные артерии, сонные артерии, Виллизиев круг, схематично представлены руки, артерии P1,P2,P3, A1,A2,A3,M1,M2,M3, коллатерали
и некоторые другие артерии. Венозный возврат представлен схематично. Влияние всей остальной
части кровеносной системы описывается «точечной» моделью.

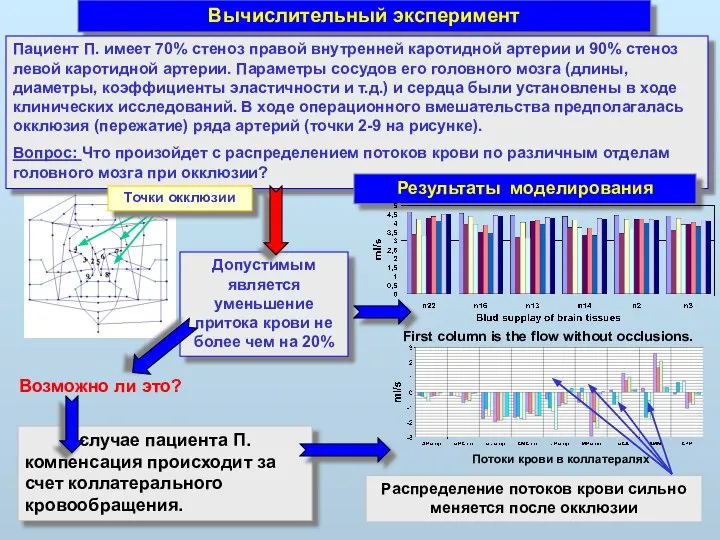
Вычислительный эксперимент
Пациент П. имеет 70% стеноз правой внутренней каротидной артерии и 90% стеноз левой каротидной артерии. Параметры сосудов его головного мозга (длины, диаметры, коэффициенты эластичности и т.д.) и сердца были установлены в ходе клинических исследований. В ходе операционного вмешательства предполагалась окклюзия (пережатие) ряда артерий (точки 2-9 на рисунке).
Вопрос: Что произойдет с распределением потоков крови по различным отделам головного мозга при окклюзии?
Результаты моделирования
Допустимым является уменьшение притока крови не более чем на 20%
Возможно ли это?
В случае пациента П. компенсация происходит за счет коллатерального кровообращения.
Распределение потоков крови сильно меняется после окклюзии
Точки окклюзии

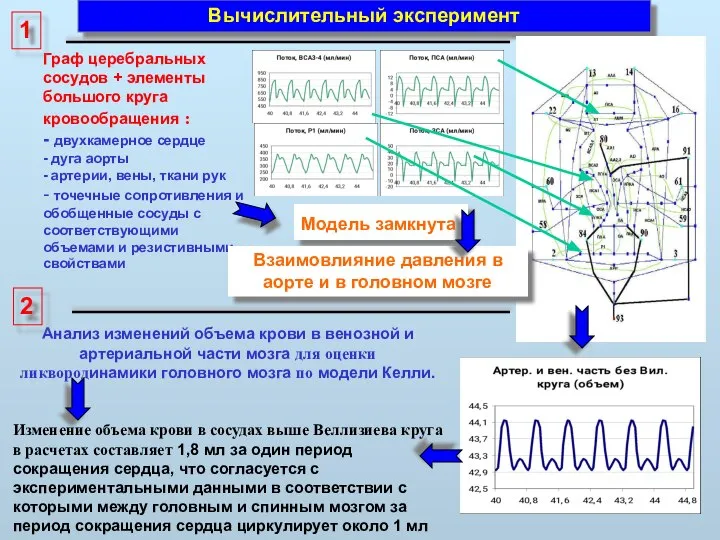
Вычислительный эксперимент
Анализ изменений объема крови в венозной и артериальной части мозга для оценки ликвородинамики головного мозга по модели Келли.
Изменение объема крови в сосудах выше Веллизиева круга в расчетах составляет 1,8 мл за один период сокращения сердца, что согласуется с экспериментальными данными в соответствии с которыми между головным и спинным мозгом за период сокращения сердца циркулирует около 1 мл ликвора.
Граф церебральных сосудов + элементы большого круга кровообращения :
- двухкамерное сердце
- дуга аорты
- артерии, вены, ткани рук
- точечные сопротивления и обобщенные сосуды с соответствующими объемами и резистивными свойствами
Модель замкнута
Взаимовлияние давления в аорте и в головном мозге
1
2

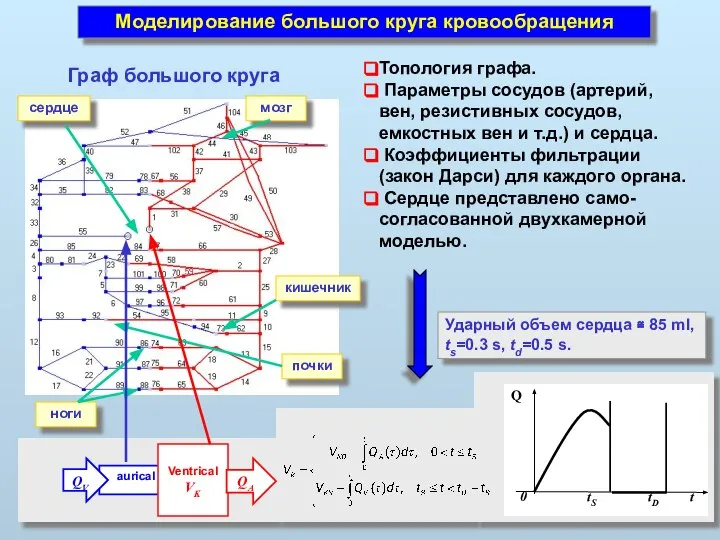
Моделирование большого круга кровообращения
сердце
почки
мозг
ноги
кишечник
Граф большого круга
Топология графа.
Параметры сосудов (артерий, вен, резистивных сосудов, емкостных вен и т.д.) и сердца.
Коэффициенты фильтрации (закон Дарси) для каждого органа.
Сердце представлено само-согласованной двухкамерной моделью.
aurical
Ventrical
VK
QA
QV
Ударный объем сердца ≅ 85 ml,
ts=0.3 s, td=0.5 s.

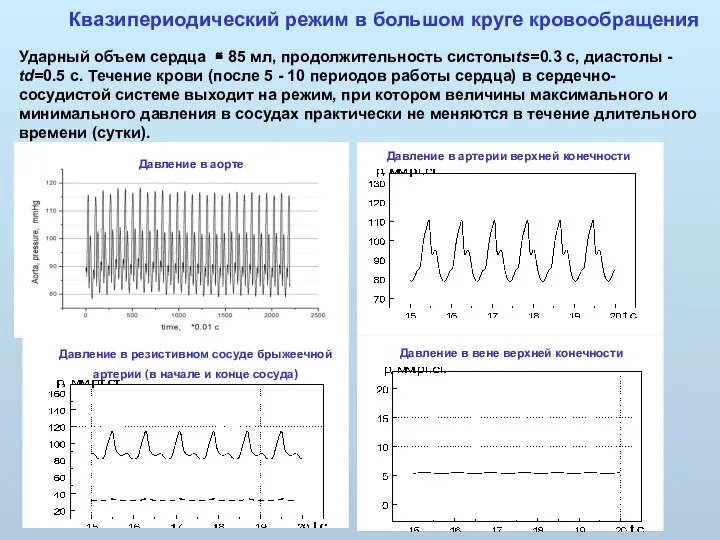
Квазипериодический режим в большом круге кровообращения
Ударный объем сердца ≅ 85 мл, продолжительность систолыts=0.3 с, диастолы - td=0.5 с. Течение крови (после 5 - 10 периодов работы сердца) в сердечно-сосудистой системе выходит на режим, при котором величины максимального и минимального давления в сосудах практически не меняются в течение длительного времени (сутки).
Давление в аорте
Давление в артерии верхней конечности
Давление в вене верхней конечности
Давление в резистивном сосуде брыжеечной артерии (в начале и конце сосуда)

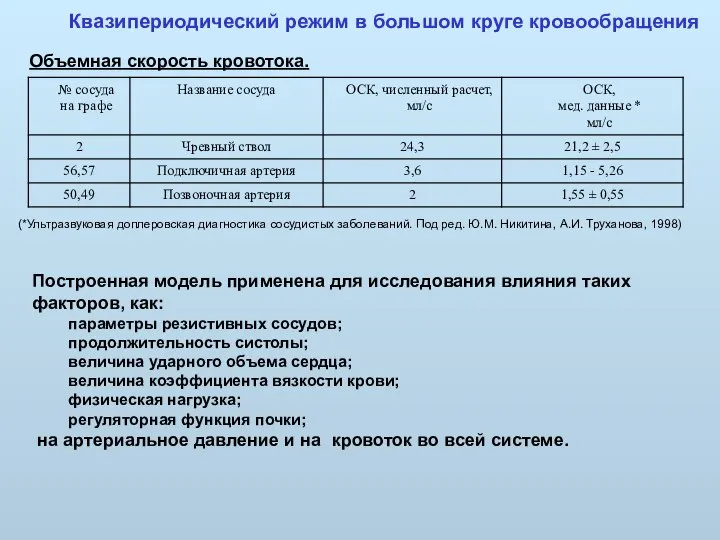
Квазипериодический режим в большом круге кровообращения
Объемная скорость кровотока.
(*Ультразвуковая доплеровская диагностика сосудистых заболеваний. Под ред. Ю.М. Никитина, А.И. Труханова, 1998)
Построенная модель применена для исследования влияния таких факторов, как:
параметры резистивных сосудов;
продолжительность систолы;
величина ударного объема сердца;
величина коэффициента вязкости крови;
физическая нагрузка;
регуляторная функция почки;
на артериальное давление и на кровоток во всей системе.

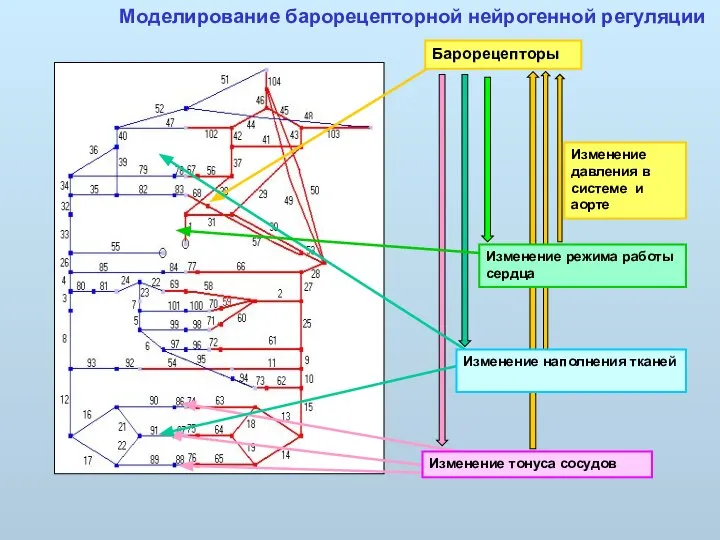
Изменение режима работы сердца
Изменение тонуса сосудов
Изменение наполнения тканей
Изменение давления в системе и аорте
Моделирование барорецепторной нейрогенной регуляции
Барорецепторы

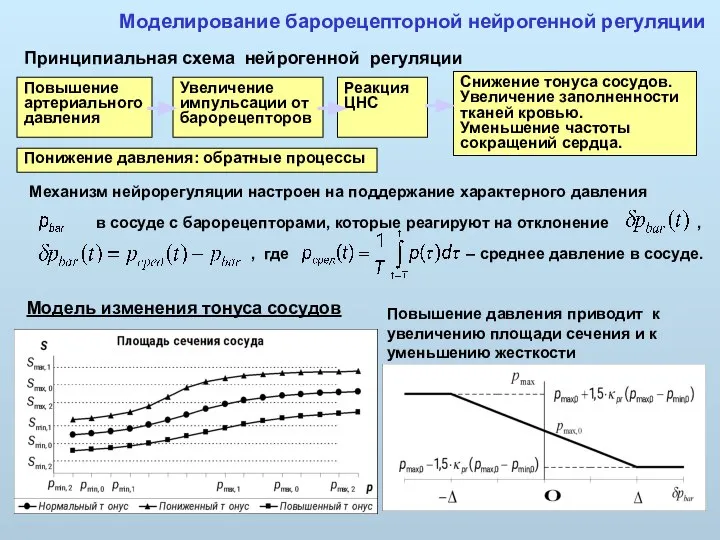
Повышение
артериального
давления
Увеличение
импульсации от
барорецепторов
Реакция
ЦНС
Снижение тонуса сосудов.
Увеличение заполненности тканей кровью.
Уменьшение частоты сокращений сердца.
Механизм нейрорегуляции настроен на поддержание характерного давления
в сосуде с барорецепторами, которые реагируют на отклонение ,
, где – среднее давление в сосуде.
Понижение давления: обратные процессы
Моделирование барорецепторной нейрогенной регуляции
Принципиальная схема нейрогенной регуляции
Модель изменения тонуса сосудов
Повышение давления приводит к увеличению площади сечения и к уменьшению жесткости

Моделирование барорецепторной нейрогенной регуляции
Модель изменения наполненности капилляров (тканей)
Повышение (уменьшение) давления приводит к увеличению (уменьшению) количества капилляров в тканях, заполненных кровью. В рамках точечных моделей это можно интерпретировать как увеличение (уменьшение) коэффициента фильтрации в законе Дарси
Модель изменения частоты сокращения сердца
Повышение (уменьшение) давления приводит к увеличению (уменьшению) продолжительности сердечного цикла tprd .

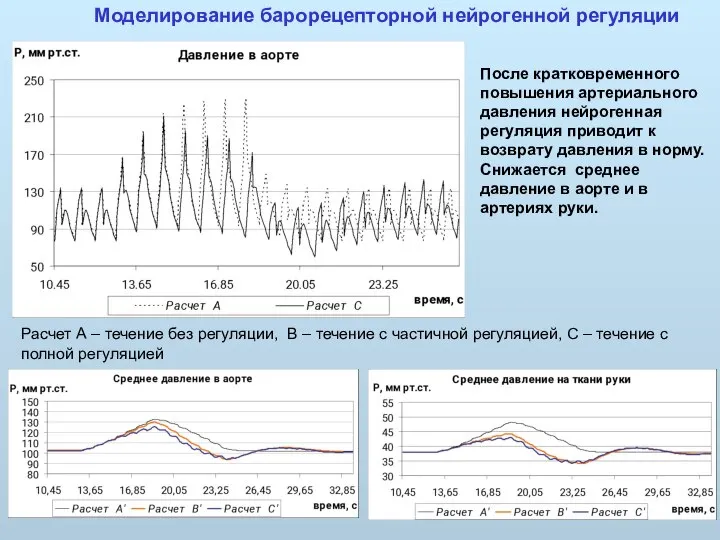
Моделирование барорецепторной нейрогенной регуляции
После кратковременного повышения артериального давления нейрогенная регуляция приводит к возврату давления в норму.
Снижается среднее давление в аорте и в артериях руки.
Расчет А – течение без регуляции, B – течение с частичной регуляцией, С – течение с полной регуляцией

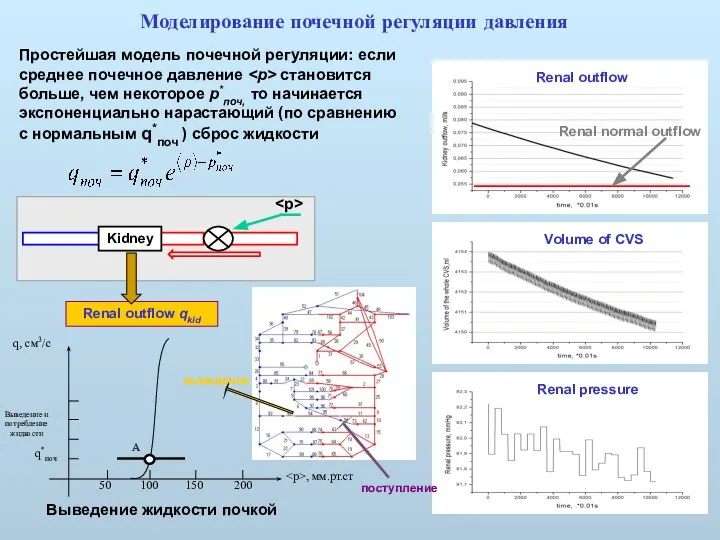
Моделирование почечной регуляции давления
Renal pressure
Volume of CVS
Простейшая модель почечной регуляции: если среднее почечное давление
становится больше, чем некоторое p*поч, то начинается экспоненциально нарастающий (по сравнению с нормальным q*поч ) сброс жидкости
Renal outflow
Выведение жидкости почкой
выведение
поступление

Получены качественные и количественные зависимости симптоматики заболевания от степени поражения сосудистой системы.
Моделирование неспецифического аортоартериита

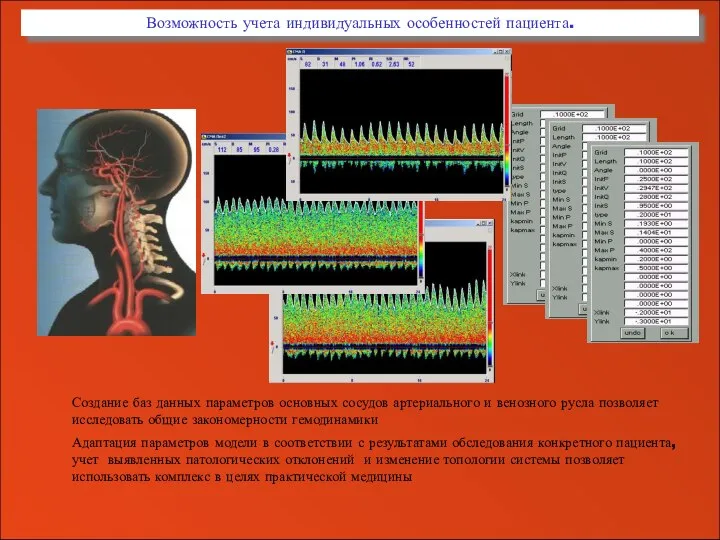
Возможность учета индивидуальных особенностей пациента.
Создание баз данных параметров основных сосудов артериального и венозного русла позволяет исследовать общие закономерности гемодинамики
Адаптация параметров модели в соответствии с результатами обследования конкретного пациента, учет выявленных патологических отклонений и изменение топологии системы позволяет использовать комплекс в целях практической медицины

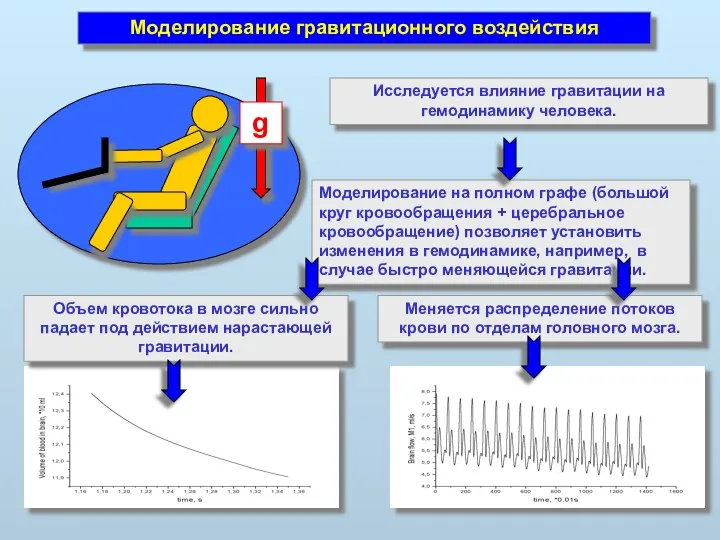
Моделирование гравитационного воздействия
Исследуется влияние гравитации на гемодинамику человека.
Моделирование на полном графе (большой круг кровообращения + церебральное кровообращение) позволяет установить изменения в гемодинамике, например, в случае быстро меняющейся гравитации.
Объем кровотока в мозге сильно падает под действием нарастающей гравитации.
Меняется распределение потоков крови по отделам головного мозга.

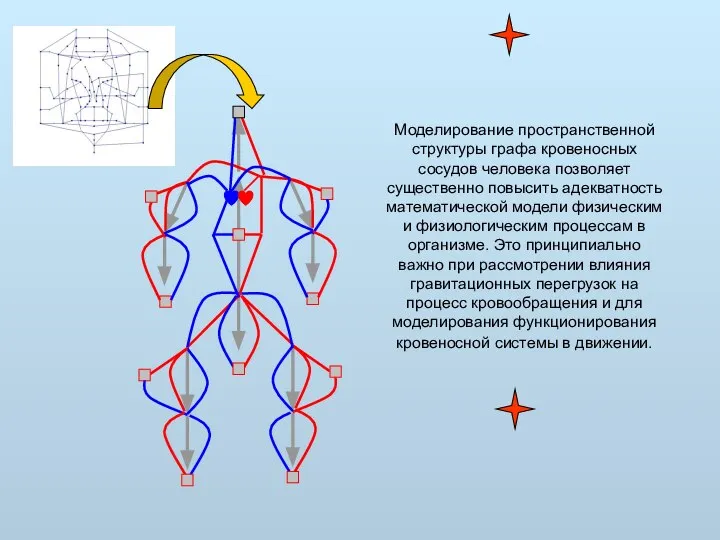
Моделирование пространственной структуры графа кровеносных сосудов человека позволяет существенно повысить адекватность математической модели физическим и физиологическим процессам в организме. Это принципиально важно при рассмотрении влияния гравитационных перегрузок на процесс кровообращения и для моделирования функционирования кровеносной системы в движении.

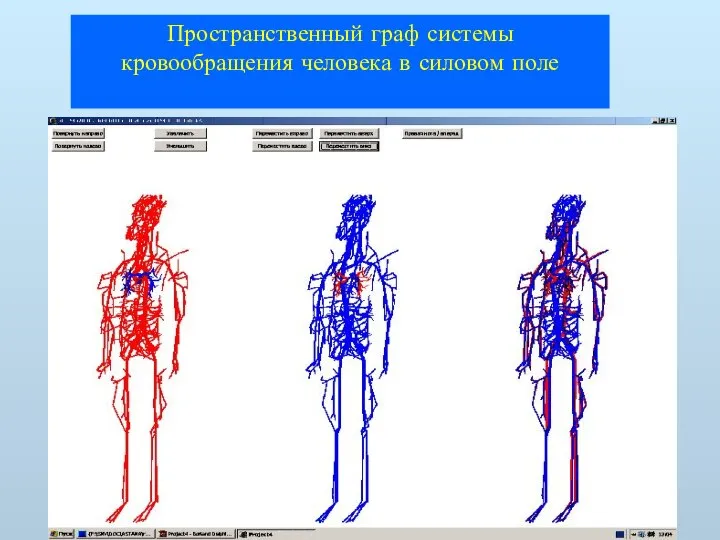
Пространственный граф системы кровообращения человека в силовом поле