Содержание
- 2. Математика – один из предметов, который вызывает значительные затруднения у большинства учащихся. В обучении детей с
- 3. Коррекционные классы созданы для обучения и воспитания детей, у которых при потенциально сохранных возможностях интеллектуального развития
- 4. Коррекционная работа с детьми должна вестись по следующим направлениям: Осуществление индивидуального подхода к детям Предотвращение наступления
- 5. Выделяют 13 этапов урока в коррекционных классах: Организационный этап(начало урока) Этап проверки домашнего задания Этап устного
- 6. Организационный этап (начало урока) Задачи этапа - обеспечить комфортную внешнюю обстановку для работы, обеспечить положительный эмоциональный
- 7. Например, домашним заданием было решить уравнения или найти нули функции 3х²-48=0 х²+4=-5х 4х²+1=0 у=3х²+х Карточки с
- 8. Этап устного счета Задачи этапа – совершенствование навыков устных вычислений; закрепление математических понятий. Если хорошо проведен
- 9. Этап устного счета 5) Возможно использовать графический диктант. Если пример решен верно, то ставим _ ,если
- 10. Этап актуализации субъективного опыта учащихся Задачи этапа- обеспечить мотивацию учения школьников; обеспе- чить включение детей в
- 11. Этап актуализации субъективного опыта учащихся Возможно выяснить тему урока следующим образом: 3+18=? 120:4=? ?·9=630 500-30=? Написать
- 12. Этап изучения нового материала Задачи этапа- обеспечить восприятие, осмысление и первичное запоминание нового материала. При изучении
- 13. Этап закрепления, тренировки и отработки умений Задачи этапа- обеспечить закрепление учащимися знаний и способов действий, которые
- 14. Этап физкультминутки или отдыха Задачи этапа- обеспечить отдых учащихся в зависимости от вида утомления; настроить детей
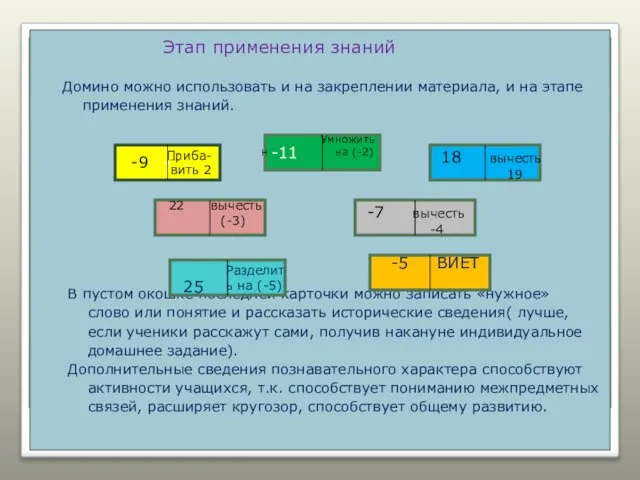
- 15. Этап применения знаний Задачи этапа - обеспечить усвоение учащимися знаний и способов деятельности на уровне их
- 16. Этап применения знаний Домино можно использовать и на закреплении материала, и на этапе применения знаний. В
- 17. Этап обобщения и систематизации знаний Задачи этапа- обеспечить формирование у учащихся не только вычислительных навыков, но
- 18. Этап информации о домашнем задании Задачи этапа- обеспечить понимание учащимися содержания и способов выполнения домашнего задания.
- 20. Скачать презентацию
















 Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит
Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит NXP semiconductors, Москва. Краткий обзор
NXP semiconductors, Москва. Краткий обзор Однофазный TIG-инвертор
Однофазный TIG-инвертор Індекси цін у будівництві
Індекси цін у будівництві Банки и банковская система РФ. Тест
Банки и банковская система РФ. Тест Прикладной Тайм-менеджмент для программистов
Прикладной Тайм-менеджмент для программистов ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет
ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет Кабинет министров
Кабинет министров Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: +
Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: + Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки
Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Перпендикуляр и наклонные
Перпендикуляр и наклонные Однородные члены предложения
Однородные члены предложения Предмет, метод, источники и принципы Трудового права
Предмет, метод, источники и принципы Трудового права Поэты Ставрополья о родном крае и о природе родного края
Поэты Ставрополья о родном крае и о природе родного края Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр
Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр Обзор на персонажа
Обзор на персонажа ВКР: Действительный цикл машины МВВ6 - 1 -2
ВКР: Действительный цикл машины МВВ6 - 1 -2 15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом).
15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом). Правила наложения жгутов повязок и шин
Правила наложения жгутов повязок и шин Вальдорфская система образования
Вальдорфская система образования Social Ecology Sustainable Development
Social Ecology Sustainable Development  Ваш профессиональный маршрут
Ваш профессиональный маршрут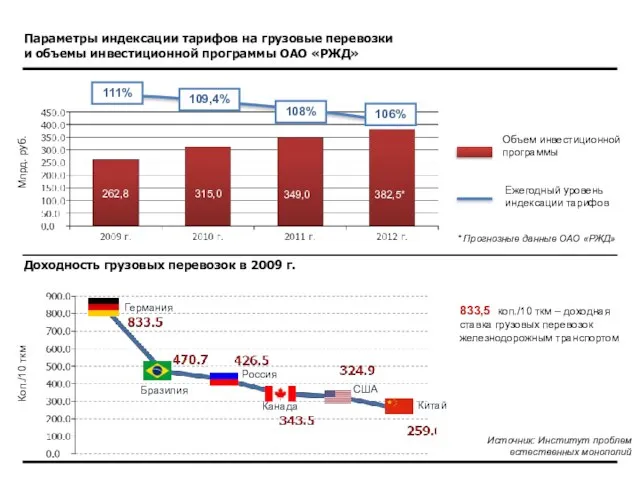 Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД»
Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД» Концепция воспитательной системы
Концепция воспитательной системы Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Презентация на тему Использования краеведческого материала в образовательном процессе
Презентация на тему Использования краеведческого материала в образовательном процессе