Содержание
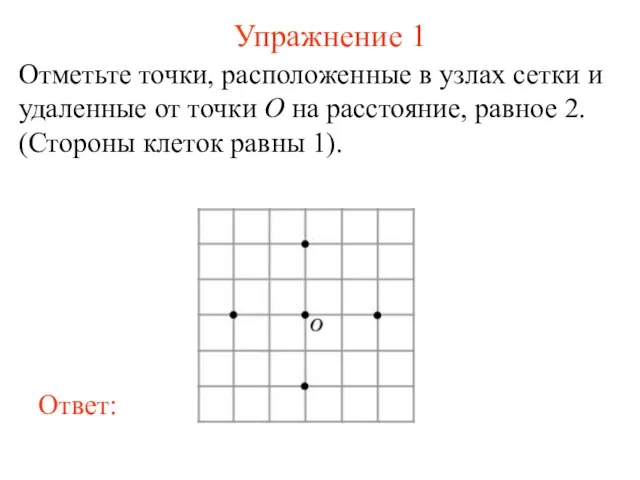
- 2. Упражнение 1 Отметьте точки, расположенные в узлах сетки и удаленные от точки O на расстояние, равное
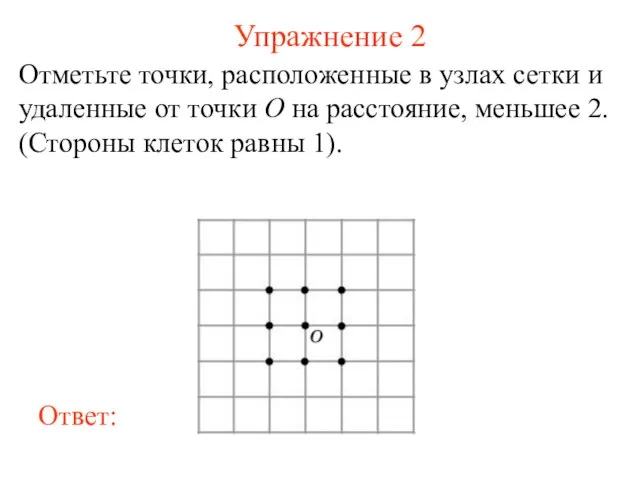
- 3. Упражнение 2 Отметьте точки, расположенные в узлах сетки и удаленные от точки O на расстояние, меньшее
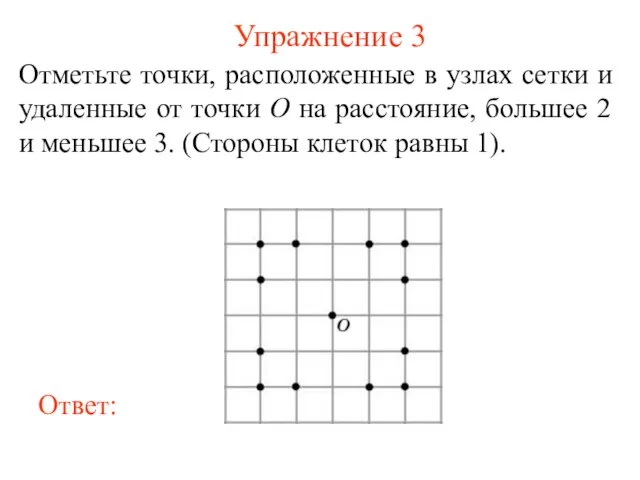
- 4. Упражнение 3 Отметьте точки, расположенные в узлах сетки и удаленные от точки O на расстояние, большее
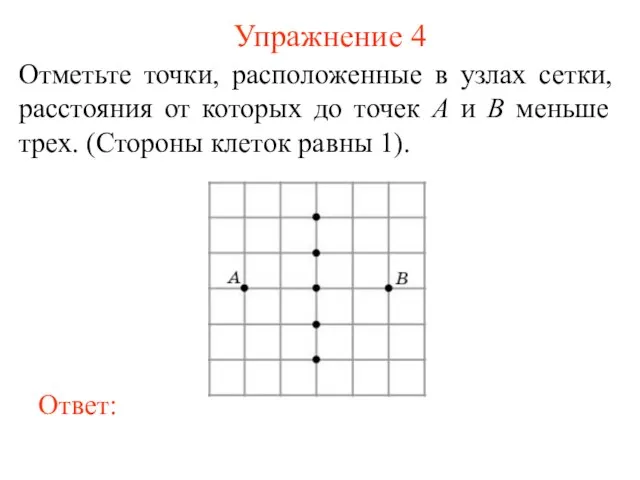
- 5. Упражнение 4 Отметьте точки, расположенные в узлах сетки, расстояния от которых до точек A и B
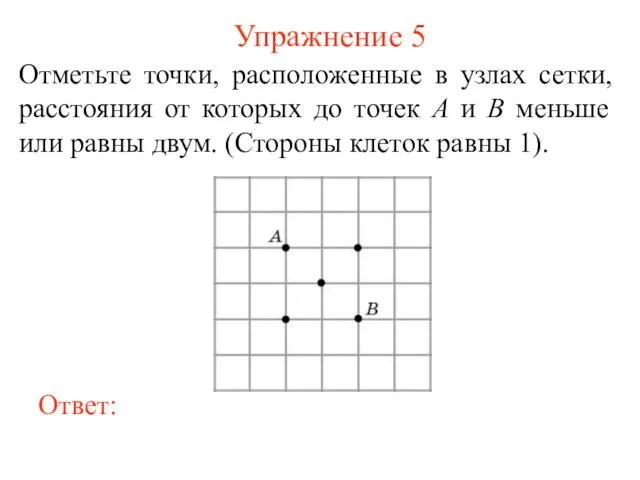
- 6. Упражнение 5 Отметьте точки, расположенные в узлах сетки, расстояния от которых до точек A и B
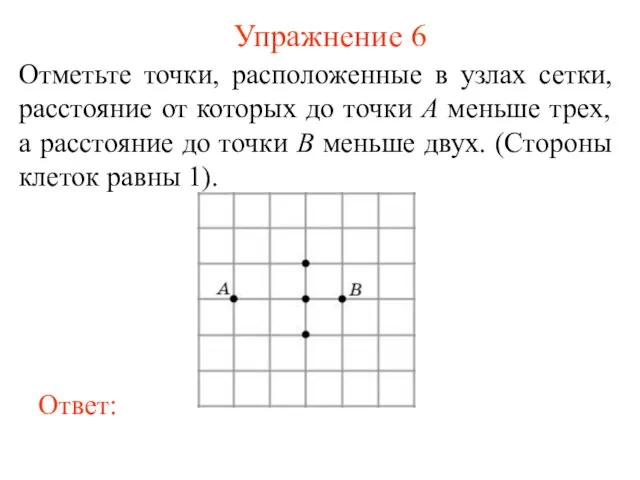
- 7. Упражнение 6 Отметьте точки, расположенные в узлах сетки, расстояние от которых до точки A меньше трех,
- 8. Упражнение 7 Отметьте точки, расположенные в узлах сетки, расстояние от которых до точки A больше двух,
- 9. Упражнение 8 Отметьте точки, расположенные в узлах сетки, расстояние от которых до точки A меньше, чем
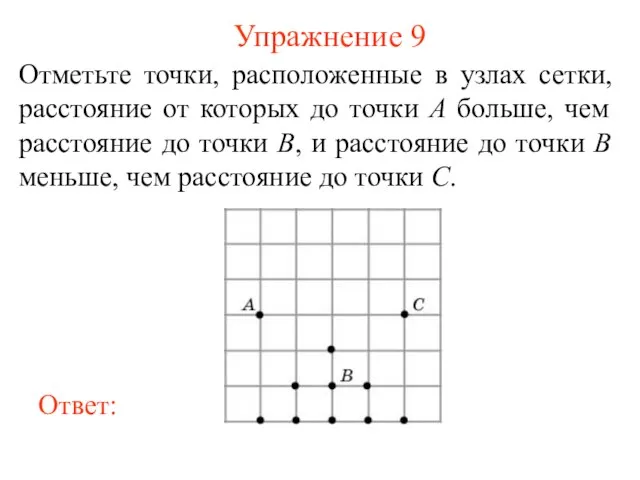
- 10. Упражнение 9 Отметьте точки, расположенные в узлах сетки, расстояние от которых до точки A больше, чем
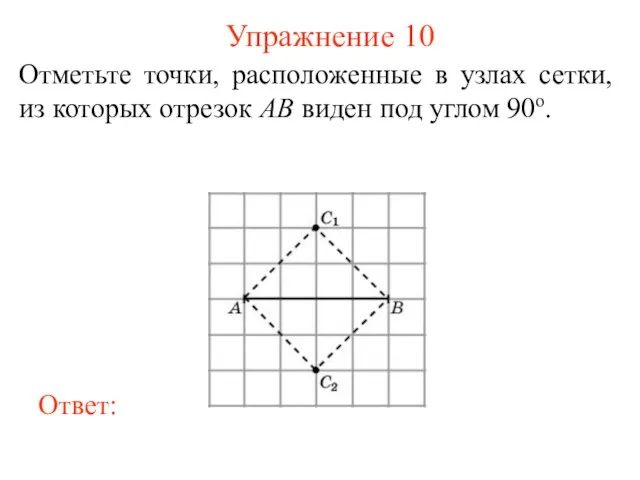
- 11. Упражнение 10 Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 90о.
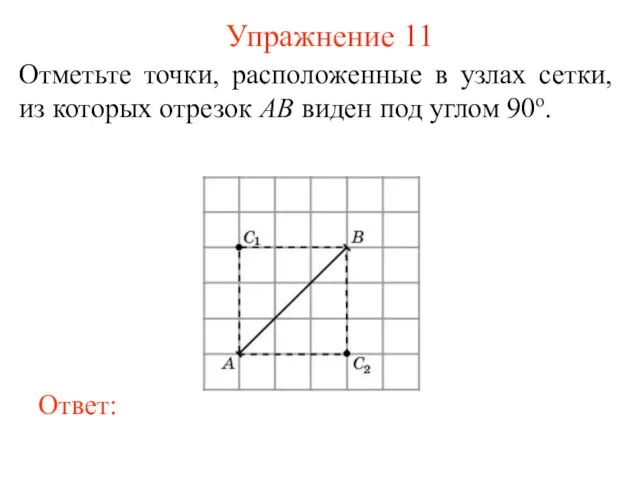
- 12. Упражнение 11 Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 90о.
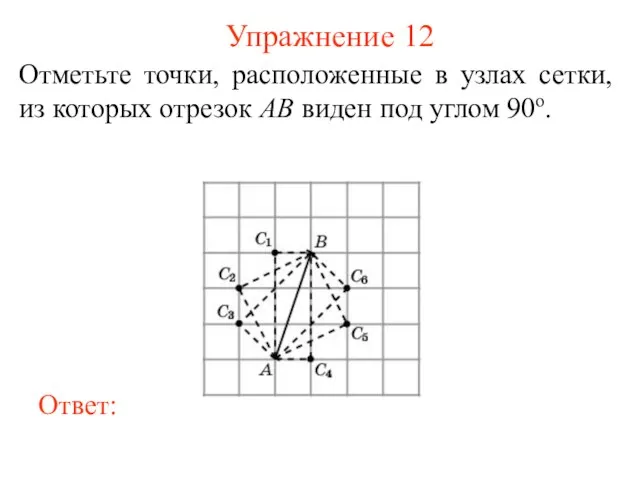
- 13. Упражнение 12 Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 90о.
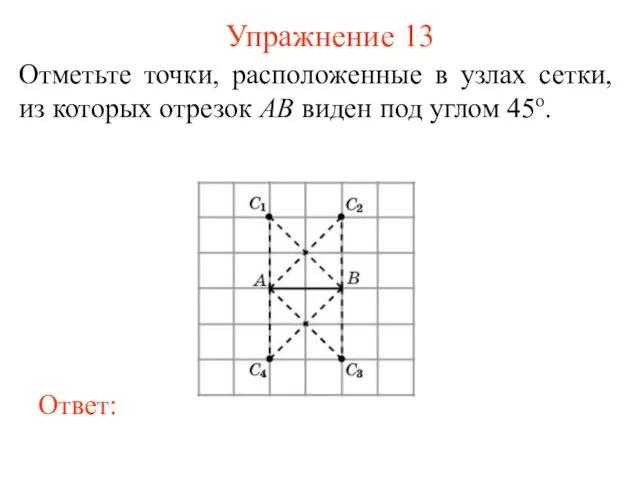
- 14. Упражнение 13 Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 45о.
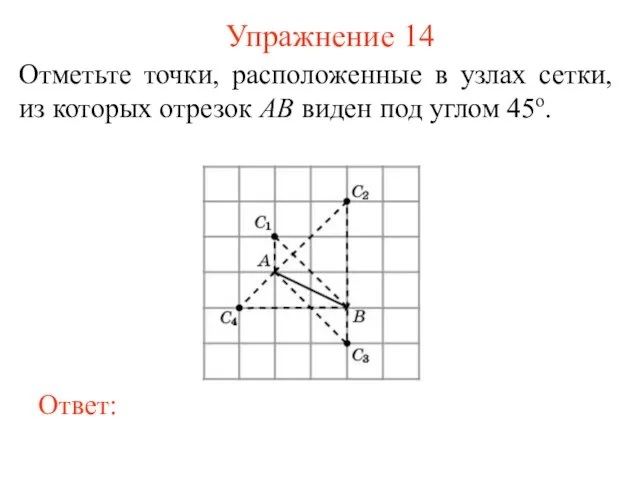
- 15. Упражнение 14 Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 45о.
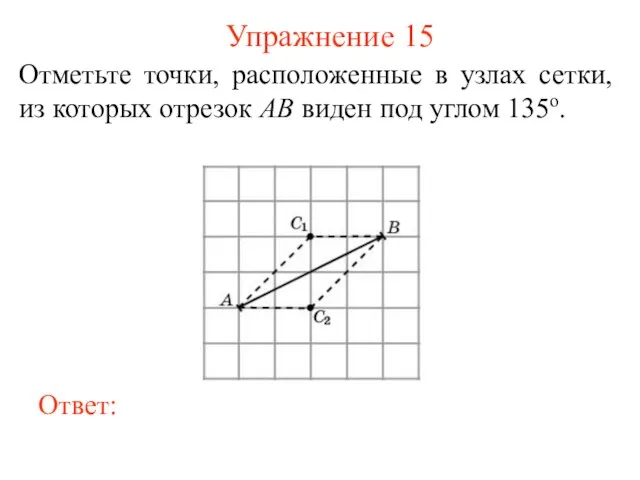
- 16. Упражнение 15 Отметьте точки, расположенные в узлах сетки, из которых отрезок AB виден под углом 135о.
- 17. Серединный перпендикуляр Теорема. Серединный перпендикуляр к отрезку является ГМТ, одинаково удаленных от концов этого отрезка. Доказательство.
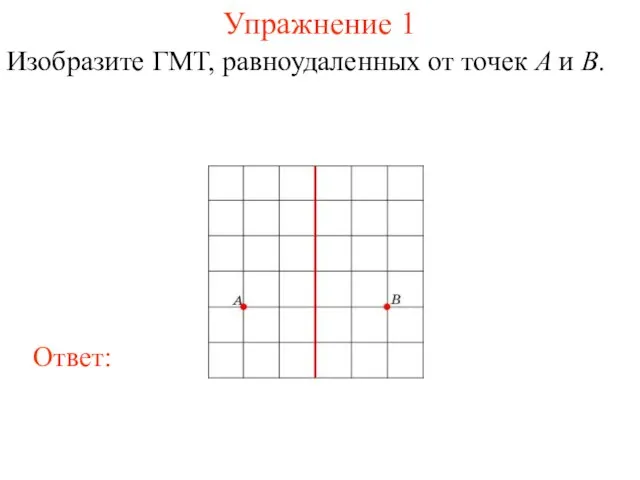
- 18. Упражнение 1 Изобразите ГМТ, равноудаленных от точек A и B.
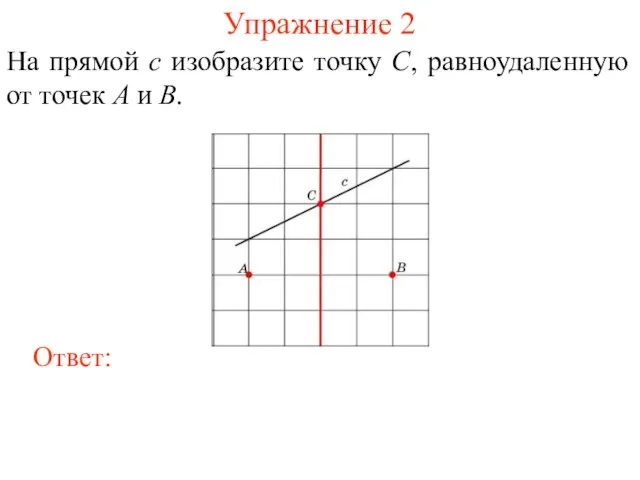
- 19. Упражнение 2 На прямой c изобразите точку C, равноудаленную от точек A и B.
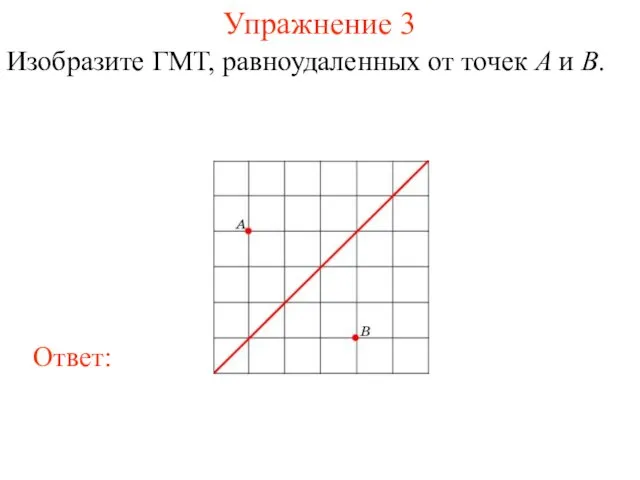
- 20. Упражнение 3 Изобразите ГМТ, равноудаленных от точек A и B.
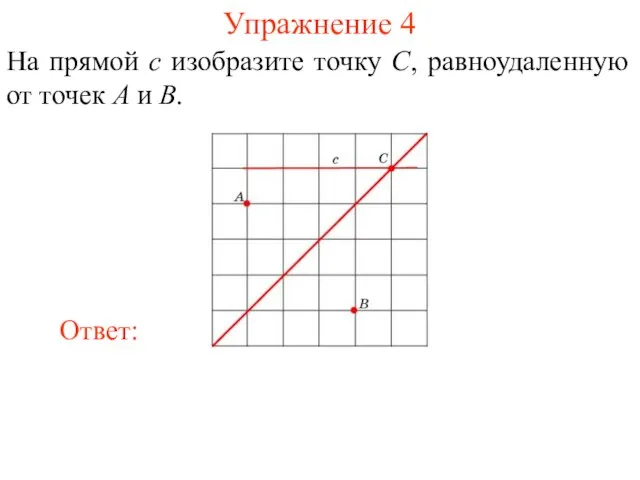
- 21. Упражнение 4 На прямой c изобразите точку C, равноудаленную от точек A и B.
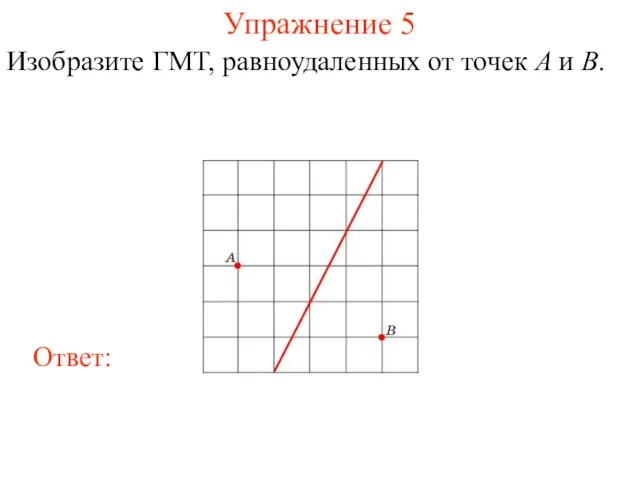
- 22. Упражнение 5 Изобразите ГМТ, равноудаленных от точек A и B.
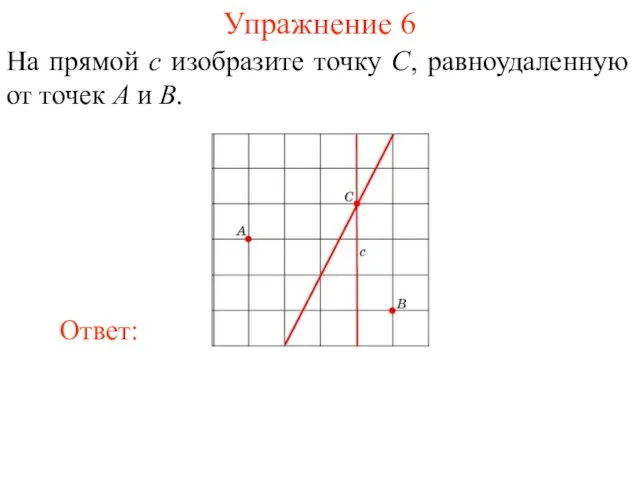
- 23. Упражнение 6 На прямой c изобразите точку C, равноудаленную от точек A и B.
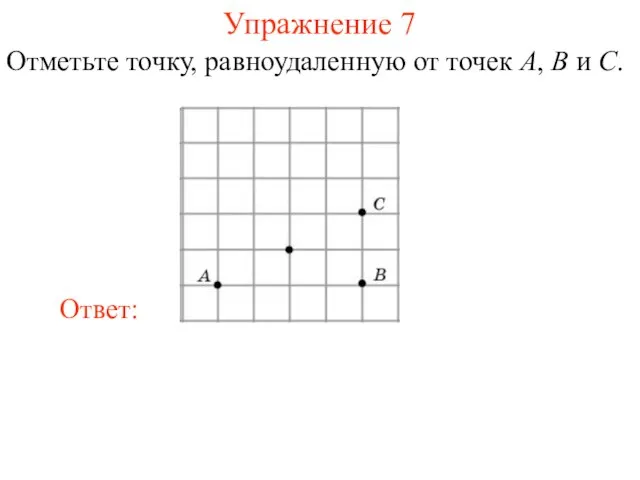
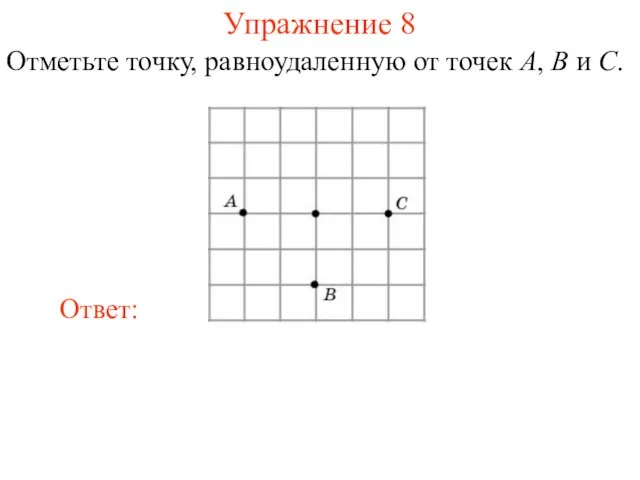
- 24. Упражнение 7 Отметьте точку, равноудаленную от точек A, B и C.
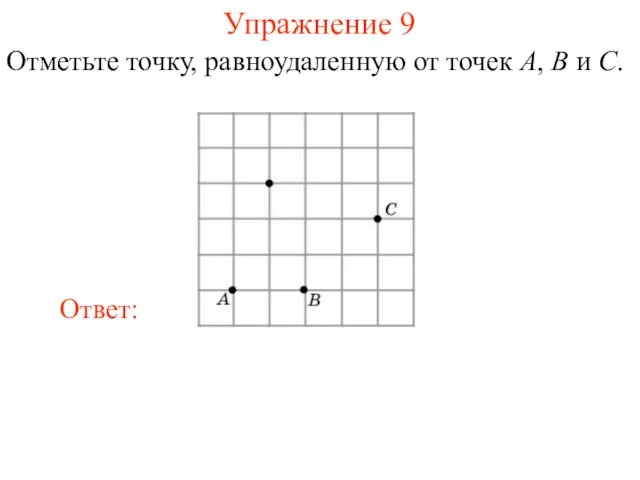
- 25. Упражнение 8 Отметьте точку, равноудаленную от точек A, B и C.
- 26. Упражнение 9 Отметьте точку, равноудаленную от точек A, B и C.
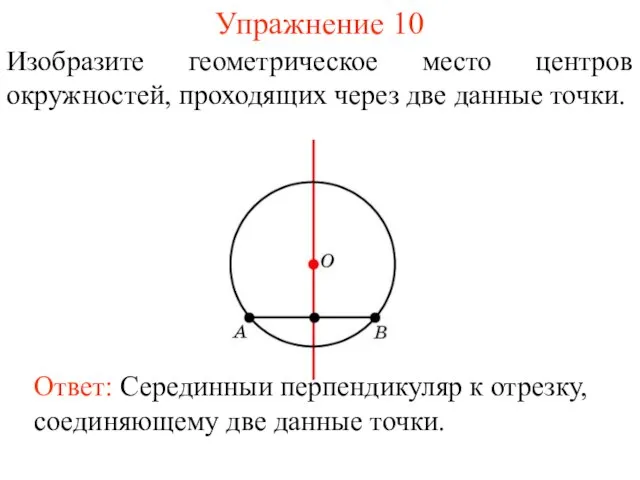
- 27. Упражнение 10 Изобразите геометрическое место центров окружностей, проходящих через две данные точки. Ответ: Серединный перпендикуляр к
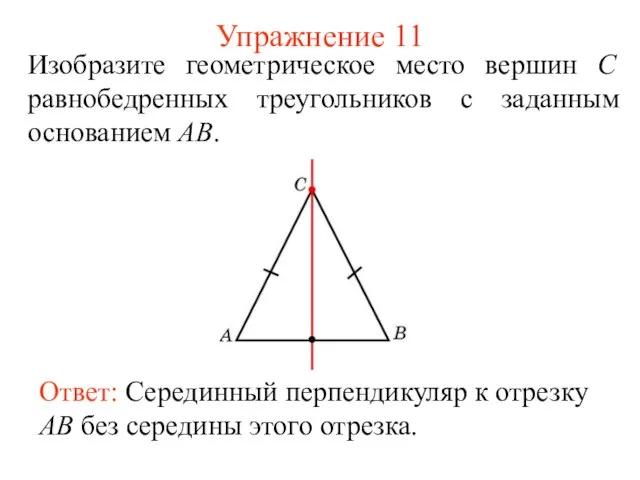
- 28. Упражнение 11 Изобразите геометрическое место вершин С равнобедренных треугольников с заданным основанием AB. Ответ: Серединный перпендикуляр
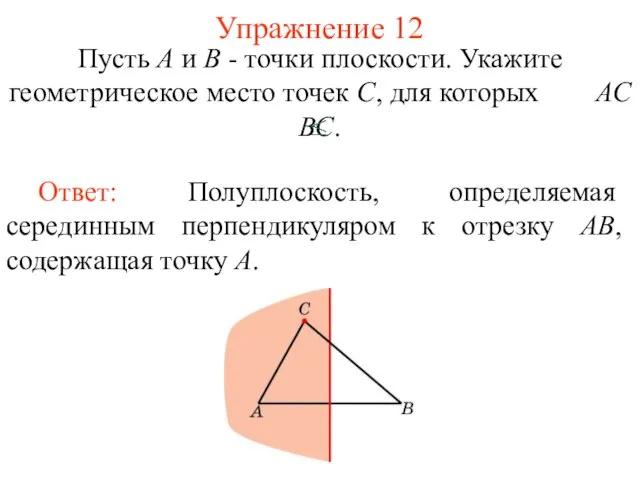
- 29. Упражнение 12 Пусть А и В - точки плоскости. Укажите геометрическое место точек С, для которых
- 30. Упражнение 13 Пусть А и В точки плоскости, c - прямая. Укажите геометрическое место точек прямой
- 31. Биссектриса угла Если CA = CB, то прямоугольные треугольники АOС и ВOС равны (по гипотенузе и
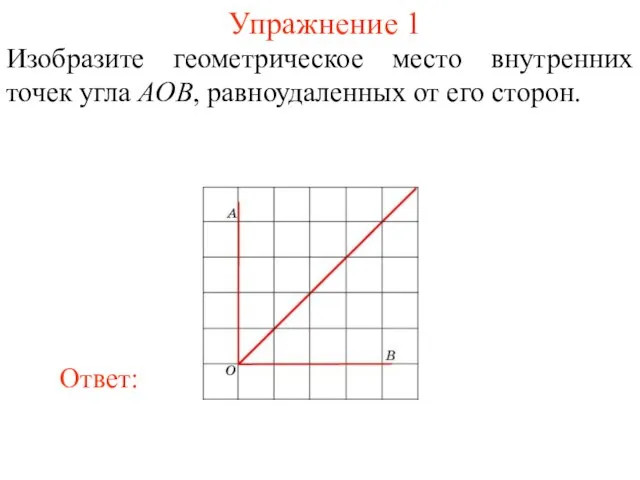
- 32. Упражнение 1 Изобразите геометрическое место внутренних точек угла AOB, равноудаленных от его сторон.
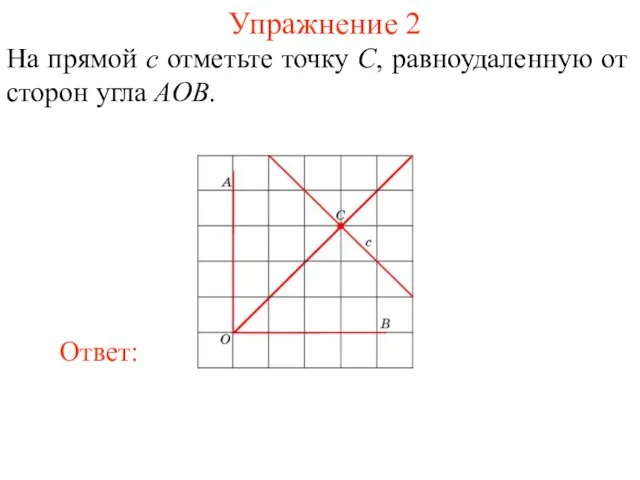
- 33. Упражнение 2 На прямой c отметьте точку C, равноудаленную от сторон угла AOB.
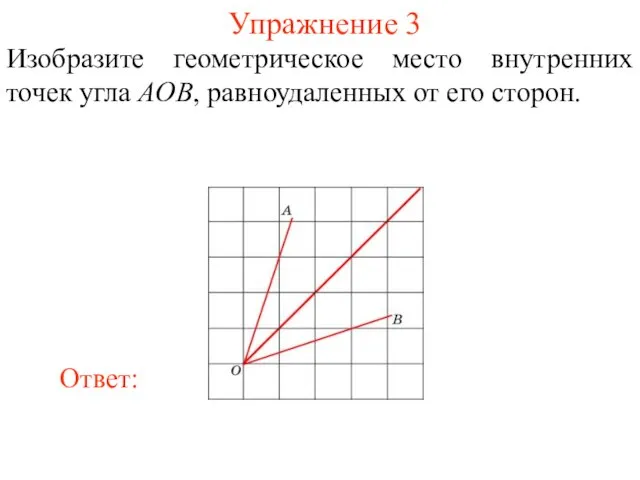
- 34. Упражнение 3 Изобразите геометрическое место внутренних точек угла AOB, равноудаленных от его сторон.
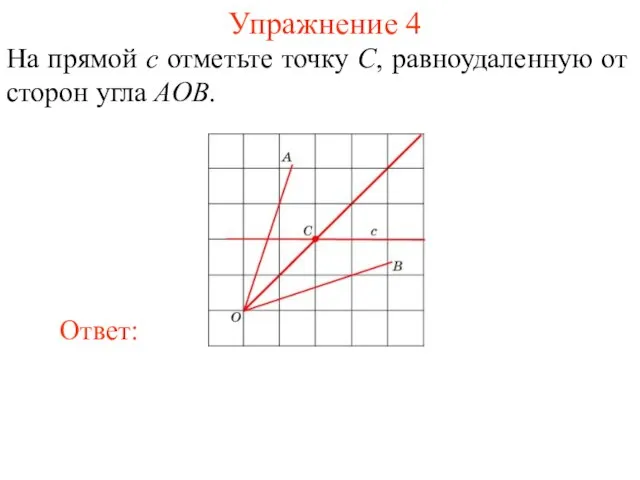
- 35. Упражнение 4 На прямой c отметьте точку C, равноудаленную от сторон угла AOB.
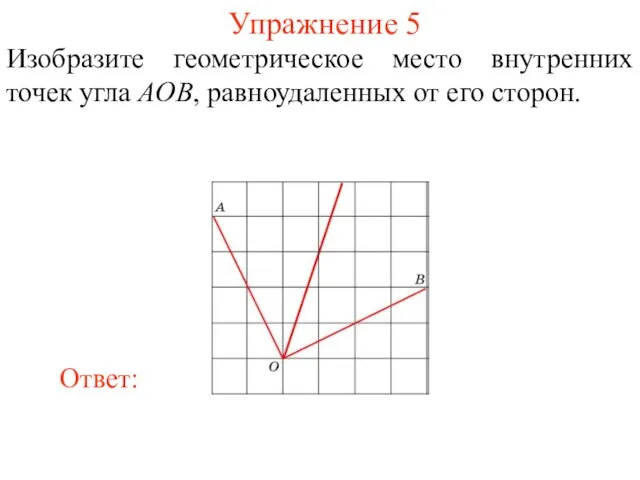
- 36. Упражнение 5 Изобразите геометрическое место внутренних точек угла AOB, равноудаленных от его сторон.
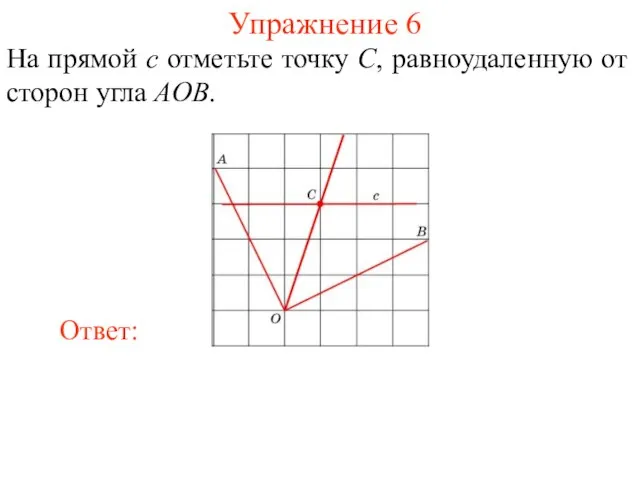
- 37. Упражнение 6 На прямой c отметьте точку C, равноудаленную от сторон угла AOB.
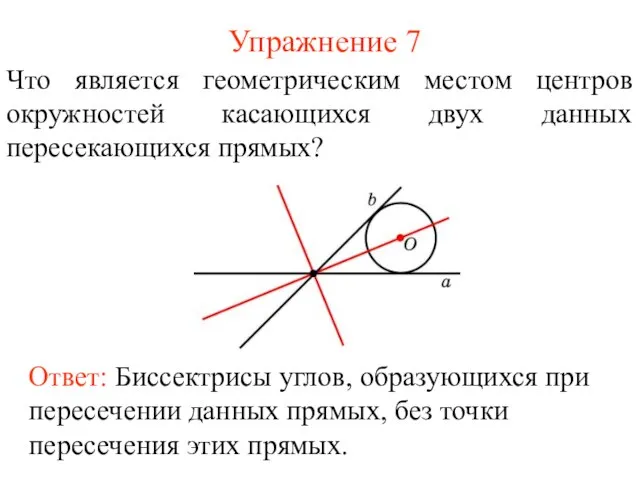
- 38. Упражнение 7 Что является геометрическим местом центров окружностей касающихся двух данных пересекающихся прямых? Ответ: Биссектрисы углов,
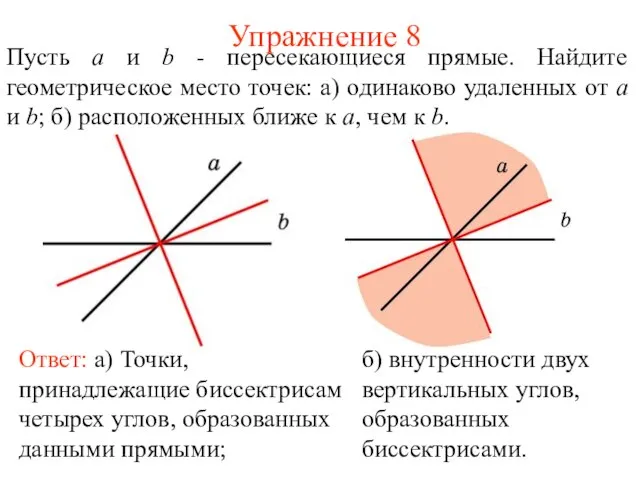
- 39. Упражнение 8 Ответ: а) Точки, принадлежащие биссектрисам четырех углов, образованных данными прямыми; б) внутренности двух вертикальных
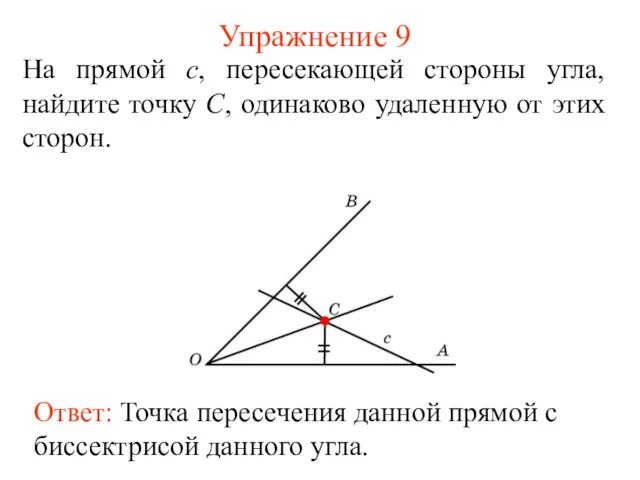
- 40. Упражнение 9 На прямой c, пересекающей стороны угла, найдите точку C, одинаково удаленную от этих сторон.
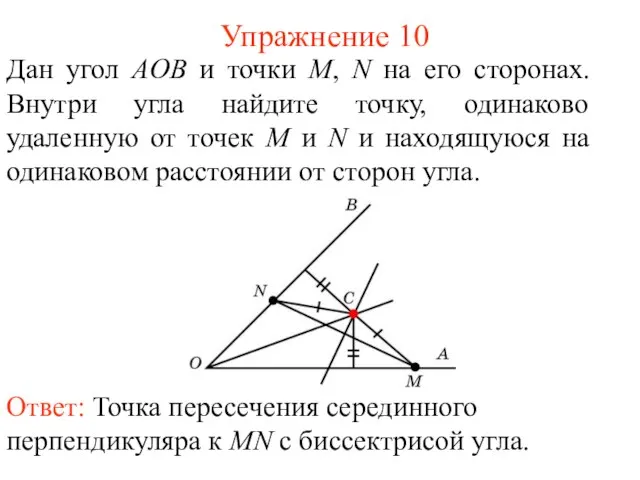
- 41. Упражнение 10 Дан угол АOB и точки M, N на его сторонах. Внутри угла найдите точку,
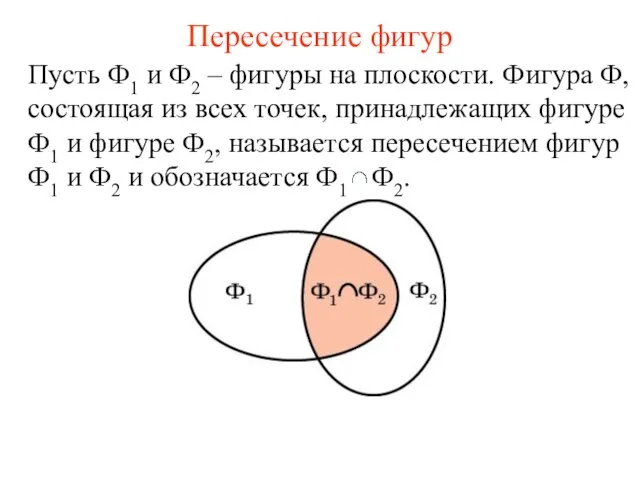
- 42. Пересечение фигур Пусть Ф1 и Ф2 – фигуры на плоскости. Фигура Ф, состоящая из всех точек,
- 43. Упражнение 1 Ответ: Искомое ГМТ является пересечением двух кругов с центрами в точках O1, O2 и
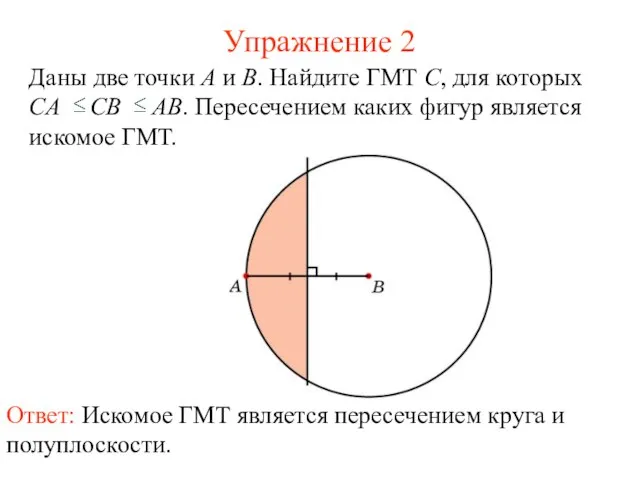
- 44. Упражнение 2
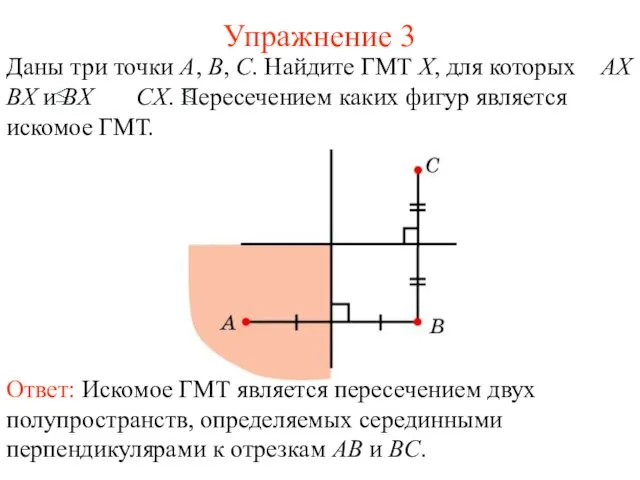
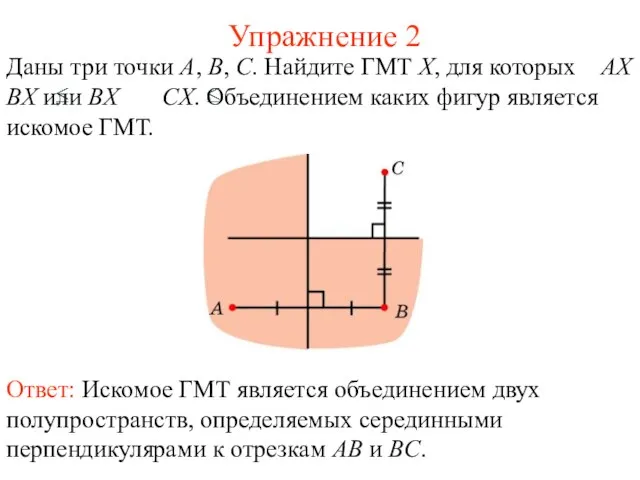
- 45. Упражнение 3 Даны три точки A, B, C. Найдите ГМТ X, для которых AX BX и
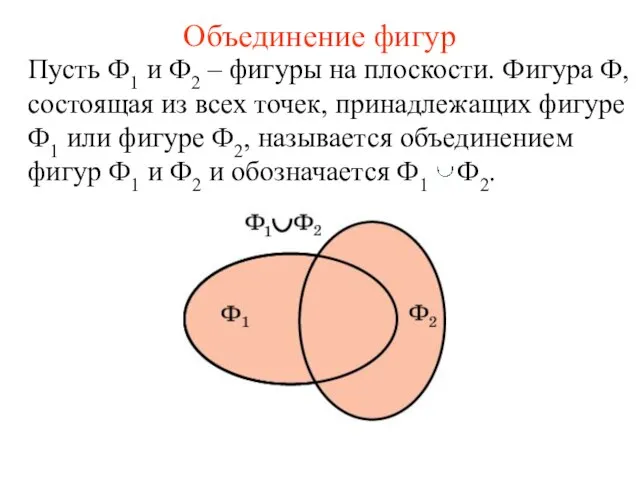
- 46. Объединение фигур Пусть Ф1 и Ф2 – фигуры на плоскости. Фигура Ф, состоящая из всех точек,
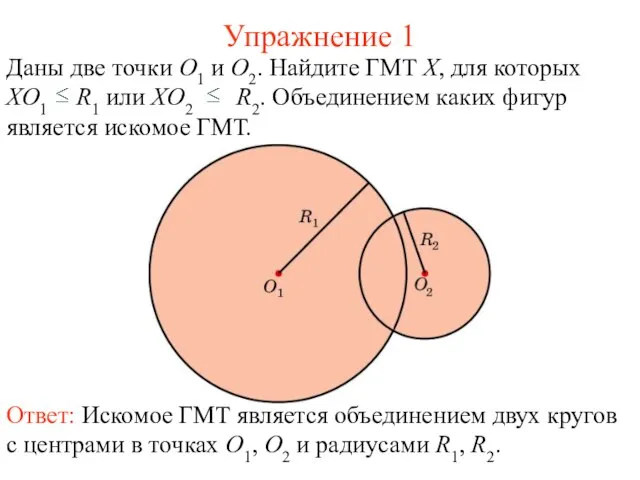
- 47. Упражнение 1 Даны две точки O1 и O2. Найдите ГМТ X, для которых XO1 R1 или
- 48. Упражнение 2 Даны три точки A, B, C. Найдите ГМТ X, для которых AX BX или
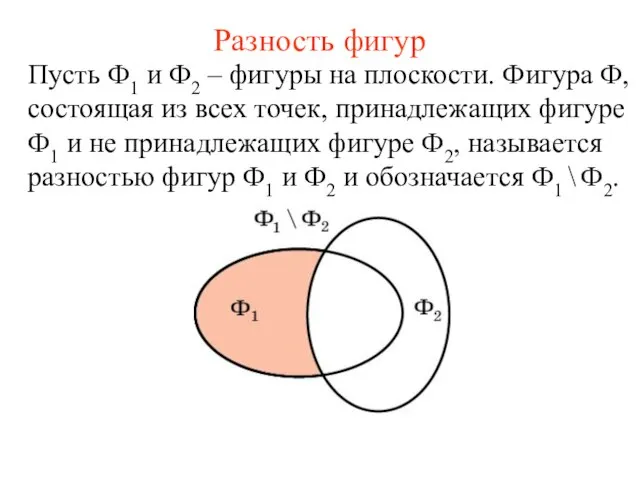
- 49. Разность фигур Пусть Ф1 и Ф2 – фигуры на плоскости. Фигура Ф, состоящая из всех точек,
- 51. Скачать презентацию






 Презентация на тему Задачи на смеси и сплавы (9 класс)
Презентация на тему Задачи на смеси и сплавы (9 класс) Русская литература XX века: общая характеристика
Русская литература XX века: общая характеристика Денежные единицы мира
Денежные единицы мира Презентация на тему Золотой век Екатерины II
Презентация на тему Золотой век Екатерины II  Доходный подход к оценке
Доходный подход к оценке Музей Конфлуанс
Музей Конфлуанс Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ
Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ Презентация на тему Технология обработки древесины
Презентация на тему Технология обработки древесины Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье
Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье Поняття ЕТ Excel
Поняття ЕТ Excel Налоги: сущность и виды. Классификация
Налоги: сущность и виды. Классификация Внутреняя энергия
Внутреняя энергия В стране правовых знаний
В стране правовых знаний Убранство русской избы
Убранство русской избы Политико-правовая теория Монтескье
Политико-правовая теория Монтескье 169601
169601 Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол
Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол Франсуа Виет и его теорема (8 класс)
Франсуа Виет и его теорема (8 класс) Может ли природа жить без человека?
Может ли природа жить без человека? Юридическая ответственность и её виды
Юридическая ответственность и её виды Осенняя одежда
Осенняя одежда Банк внешней торговли (Внешторгбанк)
Банк внешней торговли (Внешторгбанк)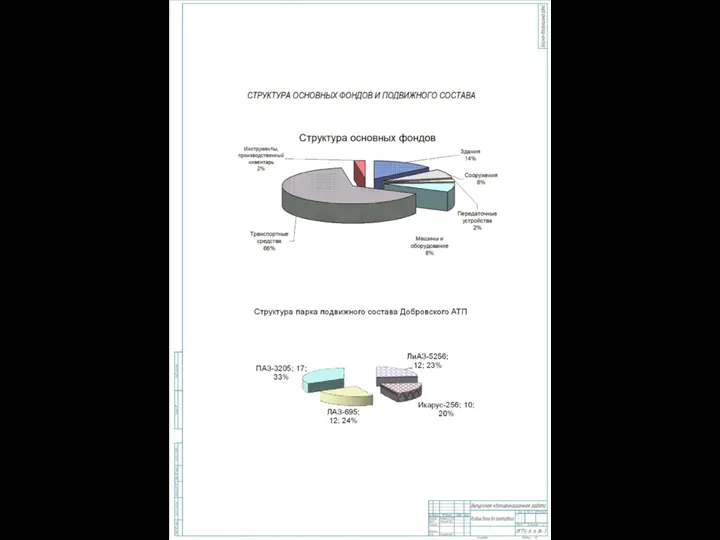 Структура основных фондов и подвижного состава
Структура основных фондов и подвижного состава Saint Isaac’s Square
Saint Isaac’s Square Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.
Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.  Педагогический совет
Педагогический совет Виды Смоленска
Виды Смоленска НАСС
НАСС