Слайд 3 Автомат – дискретный преобразователь информации, который на основе входных сигналов, поступающих в

дискретные моменты времени, и с учетом своего состояния вырабатывает выходные сигналы и изменяет свое состояние.
Под автоматом будем понимать некоторую математическую модель. Вопросы практической реализации не рассматриваются. В связи с этим при построении автоматов будем иметь в виду, что автомат функционирует в абстрактном времени и все переходы происходят мгновенно.
В зависимости от законов функционирования различают 3 вида автоматов
1. Автоматы первого рода, или автоматы Мили.
2. Автоматы второго рода.
3. Правильные автоматы второго рода, или автоматы Мура.
На практике наибольшее распространение получили автоматы Мили и автоматы Мура.
Слайд 4Задание автоматов
Автоматы могут быть заданы следующими способами:
1. В виде графа.
Рис. 1 Автомат
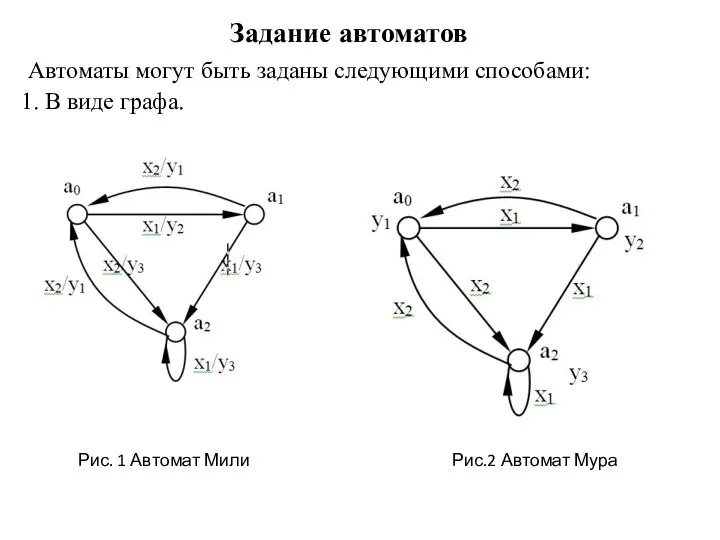
Слайд 5 При построении автомата Мили каждая дуга, соединяющая вершины ai и aj,

имеет обозначение xk/ym. Это означает следующее: находясь, в состоянии ai автомат, отрабатывая входной сигнал xk, выдает выходной сигнал ym и переходит в состояние aj.
Так как в автомате Мура выходной сигнал ym зависит только от текущего состояния aj, то каждая дуга, соединяющая вершины ai и aj, имеет обозначение xk.
Так как в автомате Мура выходной сигнал ym зависит только от текущего состояния aj, то каждая дуга, соединяющая вершины ai и aj, имеет обозначение xk.
Слайд 62 способ. В виде таблиц перехода и выхода (автомат Мили); отмеченной таблицы

перехода (автомат Мура).
Автомат Мили описывается с помощью двух таблиц: таблицы перехода и таблицы выхода:
Таблица переходов (ТП) Таблица выходов (ТВ)
Автомат Мура описывается с помощью отмеченной таблицы перехода (ТП)
Слайд 7ПРИМЕР.
Синтезировать автомат, на вход которого подаются монеты номинальной стоимостью 1, 2 и

5 рублей, а на выходе автомат выдает билет, если сумма набранных монет составляет 5 рублей, если сумма меньше 5 рублей, то автомат ничего не выдает, если сумма больше 5 рублей, то автомат возвращает деньги.
Определим входной, выходной алфавиты и множество внутренних состояний:
входной алфавит - монеты номинальной стоимостью 1, 2 и 5 рублей;
выходной алфавит Y={Н, Б, В} - на выходе возможны выходные символы: Н – ничего; Б – билет; В – возврат.
A={a0, a1, a2, a3} множество внутренних состояний ,
где a0 – начальное состояние автомата « в автомате ничего нет»;
a1 – «в автомате 1 рубль»; a2 – «в автомате 2 рубля»;
a3 – «в автомате 5 рублей».
Слайд 8Граф автомата Мили имеет вид
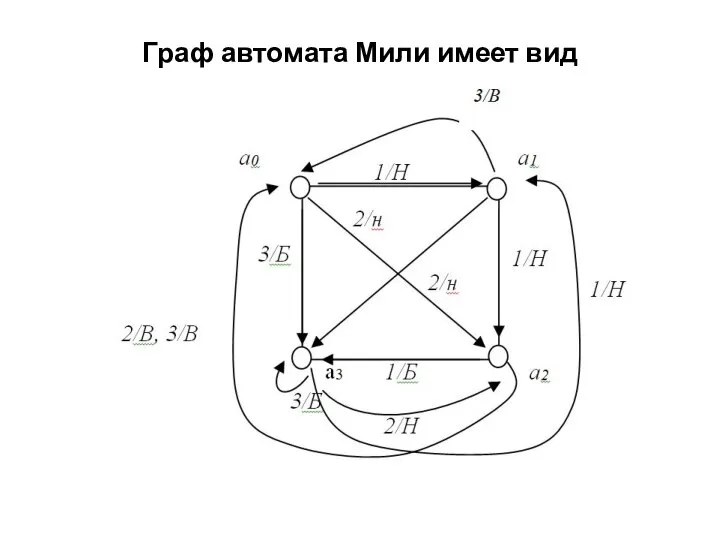
Слайд 9Таблицы перехода и выхода представлены в виде:
Таблица переходов (ТП) Таблица выходов (ТВ)
3. Автоматная
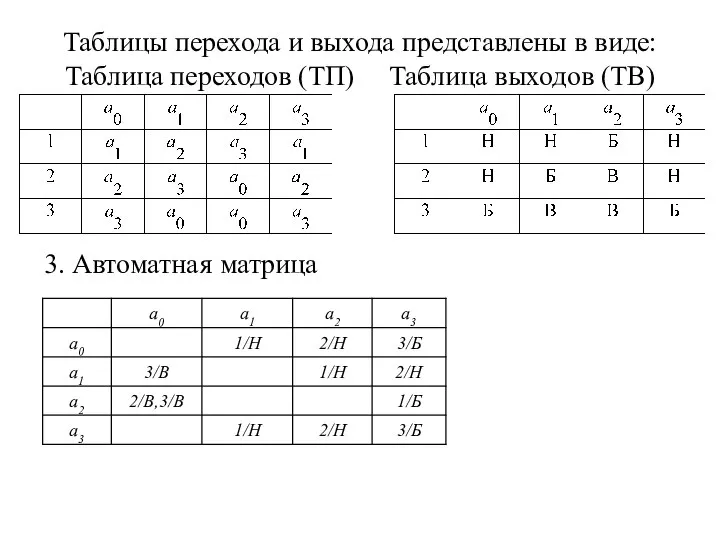
матрица
Слайд 10Неопределенным состоянием называется несуществующее состояние.
Частичным автоматом называется автомат, в котором некоторые

состояния в таблице перехода не определены. Для дальнейшего исследования неопределенное состояние некоторым образом доопределяют.
Слайд 11Минимизация автоматов
Входным словом называется совокупность сигналов, поступающих на вход.
Выходным словом называются совокупность

сигналов на выходе.
Два автомата называются эквивалентными, если они имеют одинаковый входной и выходной алфавит, и на одинаковые входные слова выдают одинаковые выходные слова.
Два состояния одноэквивалентными , если на одинаковое входное слово выдается одинаковый выходной сигнал.
Два состояния k-эквивалентными, если на одинаковое входное слово длиной в k-единиц выдается одинаковый выходной сигнал длиной в k-единиц.
Эквивалентными состояниями называются k-эквивалентные состояния для любых k.
Эквивалентные состояния объединяются в класс эквивалентности.
Минимальный автомат – это автомат, состоящий из наименьшего числа состояний, каждое из которых является классом эквивалентности исходного автомата.
Слайд 12Алгоритм минимизации автомата Мили
1. По таблице выхода находятся состояния с одинаковыми выходными

сигналами. Данные состояния объединяются в класс одноэквивалентных состояний. Проводится перекодировка.
2. По таблице перехода определяются классы двухэквивалентных состояний: для любого класса выделяется состояние, которое на одинаковый входной сигнал переходит в одинаковое состояние. Объединяем двухэквивалентные состояния в классы двухэквивалентных состояний. Проводится перекодировка.
3. Алгоритм выполняется, пока в классах k-эквивалентных состояний не находятся одинаковые состояния.
4. Вводятся новые состояния, соответствующие классам эквивалентных состояний.
5. С учетом новых состояний переписываются таблицы перехода и выхода.
Слайд 13ПРИМЕР
Пусть задан автомат Мили
Таблица выходов
Таблица переходов
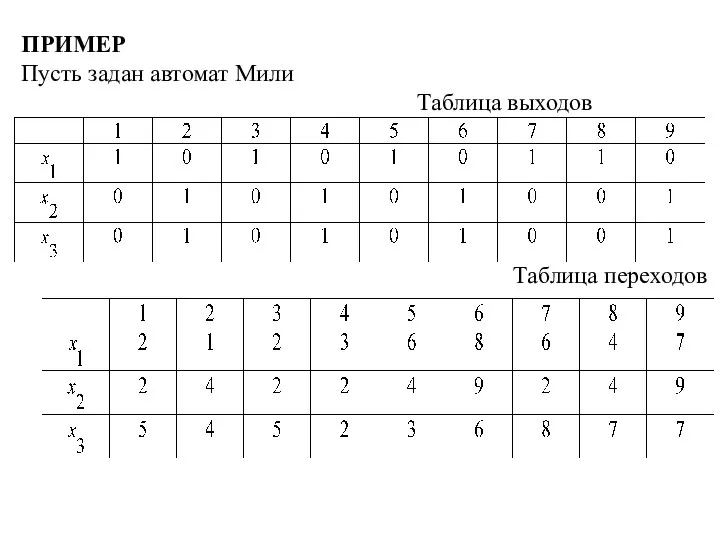
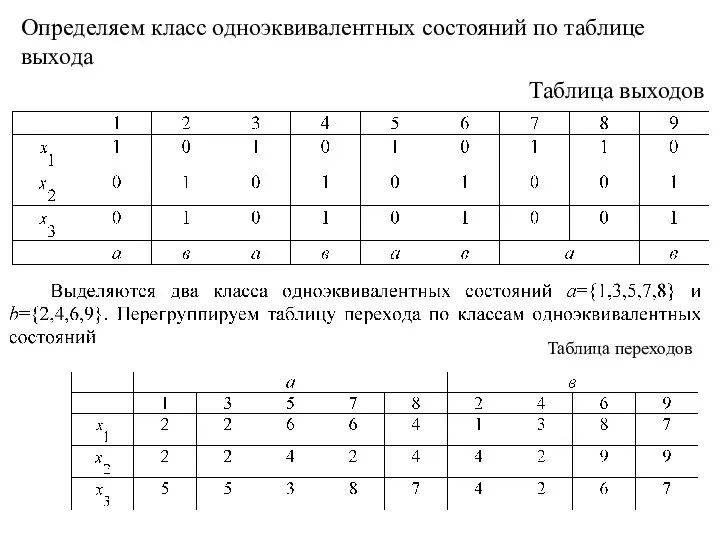
Слайд 14Определяем класс одноэквивалентных состояний по таблице выхода
Таблица выходов
Таблица переходов
Слайд 15Перекодируем состояния по полученным классам
Таблица переходов
Выделяем внутри каждого из классов одинаковые состояния,
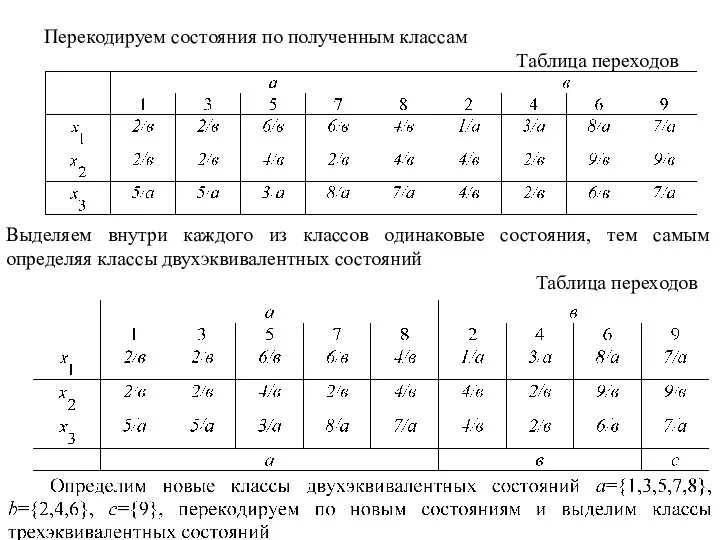
тем самым определяя классы двухэквивалентных состояний
Таблица переходов
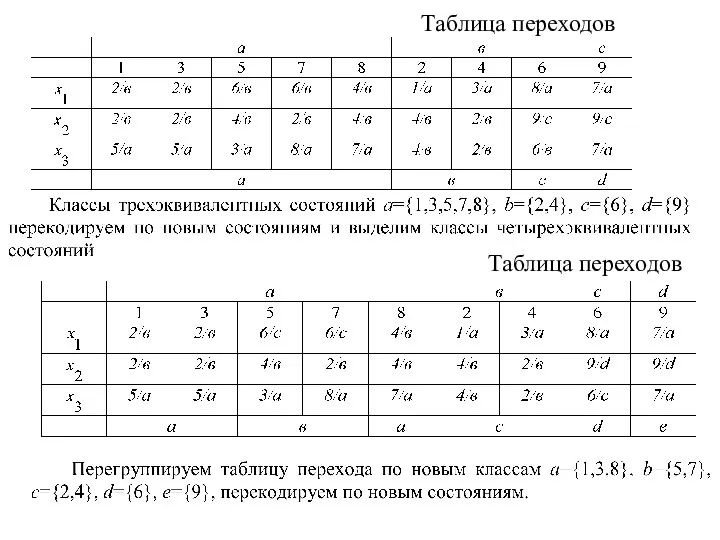
Слайд 16 Таблица переходов
Таблица переходов
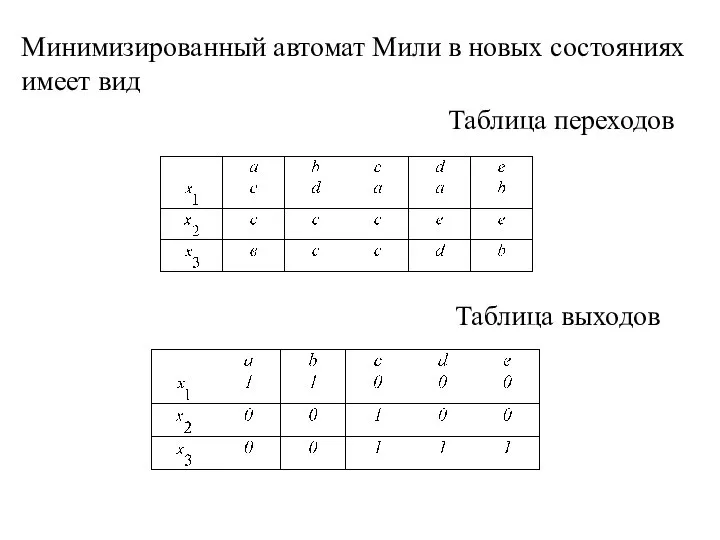
Слайд 18Минимизированный автомат Мили в новых состояниях имеет вид
Таблица переходов
Таблица выходов
Слайд 19Особенности минимизации автомата Мура
Автомат Мура минимизируется аналогично минимизации автомата Мили за исключением

первого шага. Выделение класса одноэквивалентных состояний осуществляется по строке выходов отмеченной таблицы переходов автомата Мура.
Минимизация частичных автоматов
Для того, чтобы провести минимизацию частичных автоматов неопределенное состояние доопределяется самостоятельно. Далее минимизация автоматов осуществляется по вышеизложенному алгоритму.
Слайд 20Переход от автомата Мили к автомату Мура
Автоматы Мили и автоматы Мура отличаются

функцией выхода.
Автомат Мили:
Автомат Мура:
То есть произвольному состоянию автомата Мили и входному сигналу соответствует состояние автомата Мура:
При этом начальные состояния автоматов Мили и Мура совпадают:
Таким образом, можно перекодировать таблицу перехода автомата Мили и составить отмеченную таблицу переходов автомата Мура.
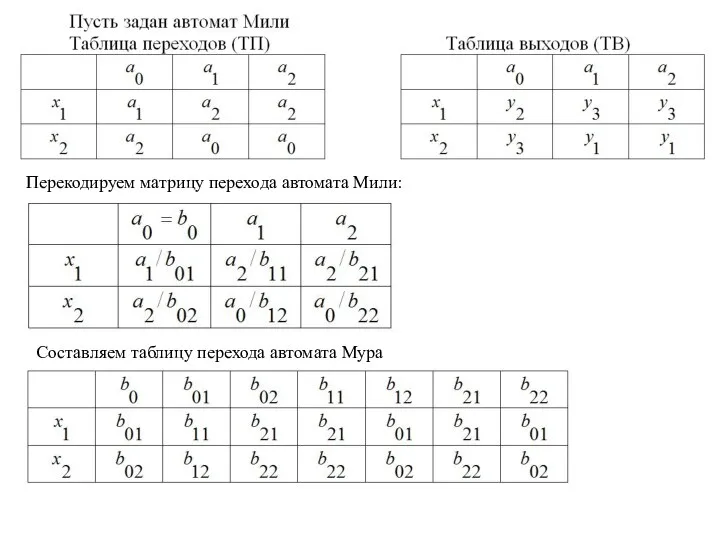
Слайд 21Перекодируем матрицу перехода автомата Мили:
Составляем таблицу перехода автомата Мура
Слайд 22При составлении таблицы перехода автомата Мили рассуждаем следующим образом: состояние автомата Мура
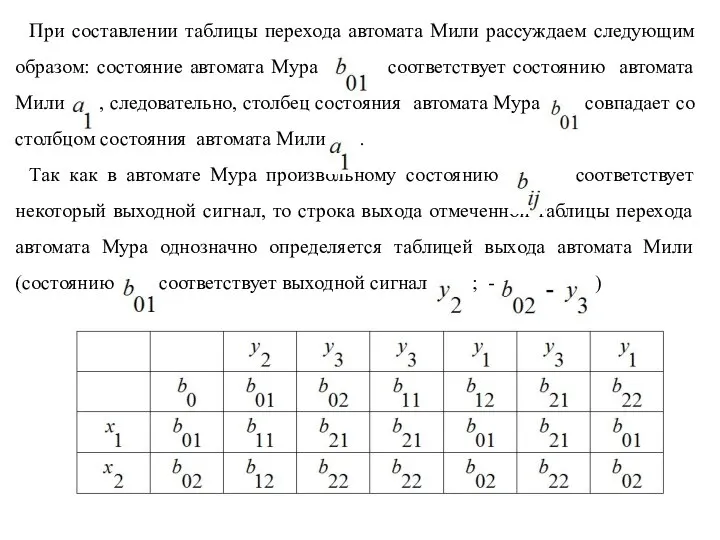
соответствует состоянию автомата Мили , следовательно, столбец состояния автомата Мура совпадает со столбцом состояния автомата Мили .
Так как в автомате Мура произвольному состоянию соответствует некоторый выходной сигнал, то строка выхода отмеченной таблицы перехода автомата Мура однозначно определяется таблицей выхода автомата Мили (состоянию соответствует выходной сигнал ; - )
Слайд 23Выходной сигнал, соответствующий состоянию , выбирается произвольно.
Если автомат Мили содержит m-состояний и
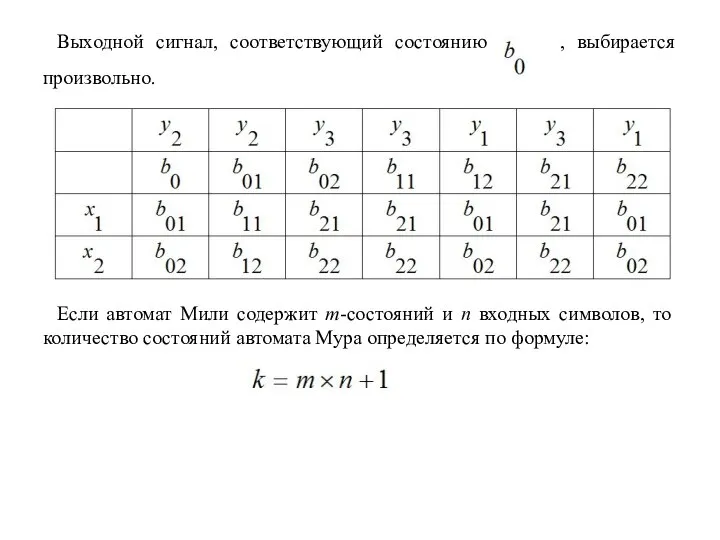
n входных символов, то количество состояний автомата Мура определяется по формуле:
Слайд 24Переход от автомата Мура к автомату Мили
Переход от автомата Мура к автомату

Мили заключается в построении таблицы выходов. Построение состоит в подстановке выходных сигналов, отмечающих состояния в отмеченной таблице переходов, вместо состояний, в которые автомат переходит.
Тем самым, если говорить в терминах графов, выходные сигналы от состояний переносятся на дуги, которые в эти состояния заходят.
А таблица переходов автомата Мили получается из отмеченной таблицы переходов автомата Мура отбрасыванием строки выходов.
Слайд 25ПРИМЕР
Пусть задан автомат Мура в виде отмеченной таблицы перехода
Данный автомат может быть
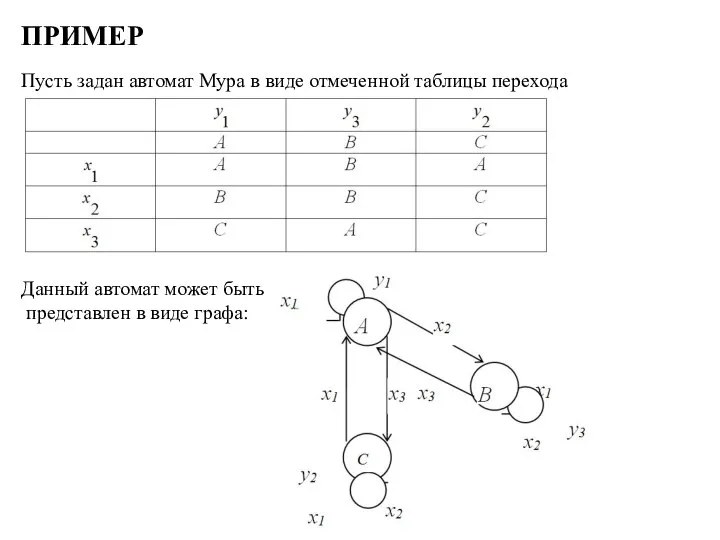
представлен в виде графа:
























 Тревожные дети
Тревожные дети Специальные захваты грузоподъёмных машин
Специальные захваты грузоподъёмных машин ООО Название компании. Шаблон презентации
ООО Название компании. Шаблон презентации Окружность, круг
Окружность, круг Влияние каллиграфии на мозговую активность. 3 часть
Влияние каллиграфии на мозговую активность. 3 часть Законодательствов области обращенияс опасными отходами
Законодательствов области обращенияс опасными отходами Mon métier
Mon métier КУЛЬТУРА ЗАПАДНОЕВРОПЕЙСКОГОСРЕДНЕВЕКОВЬЯ
КУЛЬТУРА ЗАПАДНОЕВРОПЕЙСКОГОСРЕДНЕВЕКОВЬЯ Спортивный коллектив
Спортивный коллектив Приемы сжатия текста
Приемы сжатия текста презент орелй
презент орелй Організація дистанційного навчання, за допомогою платформи MOODLE
Організація дистанційного навчання, за допомогою платформи MOODLE Метод полуреакций или электронно-ионного баланса
Метод полуреакций или электронно-ионного баланса Дистанционное обучение
Дистанционное обучение Перспективы развития платежной системы Банка России в свете Федерального закона «О национальной платежной системе»
Перспективы развития платежной системы Банка России в свете Федерального закона «О национальной платежной системе» Used Car Market in India – A Quikr Review
Used Car Market in India – A Quikr Review Биография и творчество А. А. Вознесенского
Биография и творчество А. А. Вознесенского ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «МОСКОВ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «МОСКОВ Смерть и оживление
Смерть и оживление Аренда земельных участков
Аренда земельных участков Презентация на тему Таможня в 21-ом веке
Презентация на тему Таможня в 21-ом веке Динамика уровня экономического и социального развития Санкт-Петербурга
Динамика уровня экономического и социального развития Санкт-Петербурга 2
2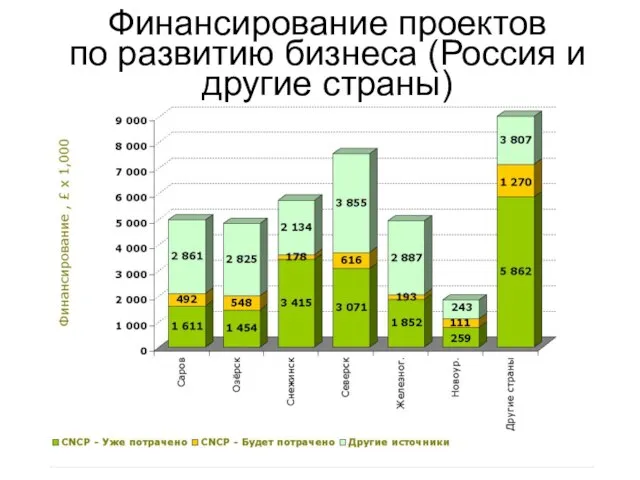 Финансирование проектов по развитию бизнеса (Россия и другие страны)
Финансирование проектов по развитию бизнеса (Россия и другие страны) ??????? ????????????????
??????? ???????????????? Рациональные уравнения
Рациональные уравнения Russian Fashion Retail Forum
Russian Fashion Retail Forum Применение жиров
Применение жиров