Линия

Линии занимают особое положение в начертательной геометрии. Используя линии можно создать наглядные модели многих процессов и проследить их течение во времени. Линия позволяет установить и исследовать функциональную зависимость между различными величинами. Кроме самостоятельного значения линия широко используется при конструировании поверхностей различных технических форм.
При определении геометрических фигур в геометрии принято исходить из основных понятий – точка, прямая, плоскость, расстояние. На основании этого линия – траектория перемещения точки. Если учесть, что положение точки при ее движении будет зависеть от непрерывно меняющейся величины d – расстояния до точки от начала координат (параметр), то линия – есть непрерывное однопараметрическое множество точек (рис. 2.1).
1. Прямые общего и частного положения. Следы прямой.
Рис. 2.1

Простейшей линией является прямая. Прямая линия в пространстве вполне определяется положением двух любых ее точек, либо двумя пересекающимися плоскостями.
Для того, чтобы построить эпюр прямой линии, достаточно построить проекции двух ее точек и провести через одноименные проекции точек проекции прямой.
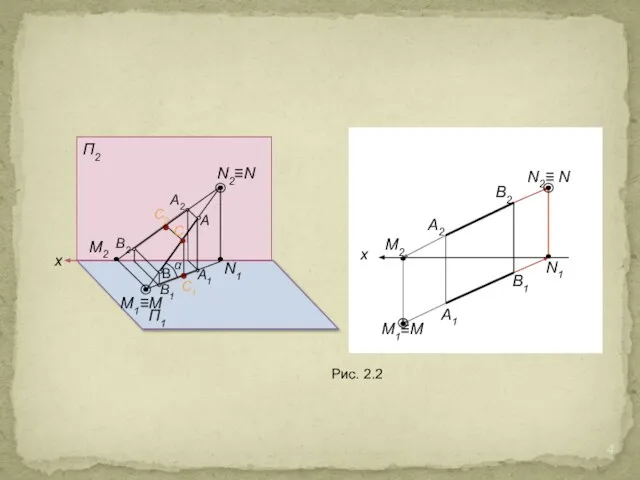
На рис. 2.2 отрезок прямой АВ занимает произвольное положение относительно всех плоскостей проекций. Такая прямая называется прямой общего положения. У нее угол наклона к плоскостям проекций не равен 90° и она пересекает все плоскости проекций. Отрезок прямой общего положения проецируется на плоскость проекций с искажением: А1В1 = cosα·АВ. Проекция отрезка прямой общего положения всегда меньше длины самого отрезка. Точка пересечения прямой с плоскостью проекций называется следом прямой.
Положение точки относительно прямой
Известно, что точка принадлежит прямой, следовательно одноименные проекции точки будут принадлежать одноименным проекциям прямой.
И если точка делит отрезок в определенном отношении, то проекции точки делят проекции отрезка прямой в том же соотношении.
((·) С Є [АВ] ^ С1 Є [А1В1] ^ С2 Є [А2В2]) => АС/СВ = А1С1/С1В1 = А2С2/С2В2 = m/n

Рис. 2.2

Прямые частного положения
Если прямая в пространстве параллельна и (или) перпендикулярна какой-либо плоскости проекций, то такая прямая называется прямой частного положения.
К прямым частного положения относятся прямые уровня и проецирующие прямые.
Прямые уровня – прямые, параллельные какой-либо плоскости проекций (рис. 2.3). В частных случаях прямые могут лежать в плоскостях проекций – линии нулевого уровня.
Проецирующие прямые – перпендикулярные какой-либо плоскости проекций (дважды прямые уровня) (рис. 2.4). Частный случай – прямые лежат на осях проекций.

Горизонталь (h)
Фронталь (f)
Профильная прямая уровня
(задается только отрезком)
h1- н.в.
h║П1 (h2 ║ x; h2, h3 ┴ z)
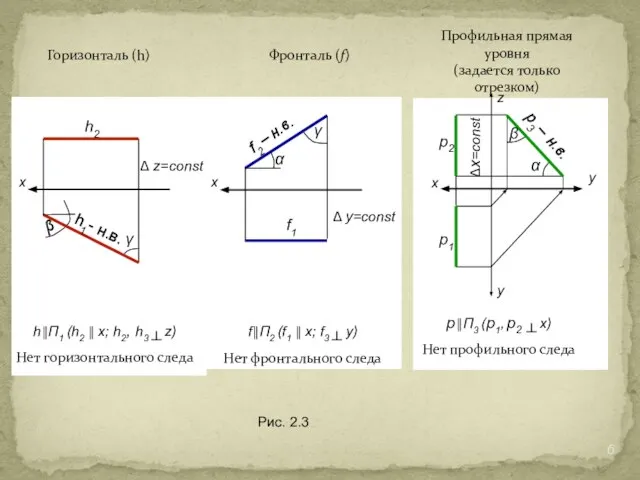
Нет горизонтального следа
∆ z=const
f║П2 (f1 ║ x; f3 ┴ y)
Нет фронтального следа
∆ y=const
∆x=const
p║П3 (p1, p2 ┴ x)
Нет профильного следа
Рис. 2.3

Горизонтально-проецирующая прямая
Фронтально-проецирующая прямая
Профильно-проецирующая прямая
Рис. 2.4
a2-н.в.
a ┴ П1
(а2, а3 ║ z; а2 ┴ x)
∆ y=const, ∆x=const
b1-н.в.
b ┴ П2
(b1, b3 ║y; b1 ┴ x)
∆x=const, ∆ z=const
с ┴ П3
(с1, с2 ║ x;)
∆ y=const, ∆ z=const

Две прямые в пространстве могут быть взаимно параллельны, пересекаться или скрещиваться (рис. 2.5).
2. Взаимное положение прямых
Параллельные прямые лежат в одной плоскости и не имеют общей точки (их одноименные проекции параллельны)
Пересекающиеся прямые лежат в одной плоскости и имеют общую точку (их одноименные проекции пересекаются)
Скрещивающиеся прямые не лежат в одной плоскости и не имеют общей точки
Рис. 2.5
a║b => a1║b1,
a2║b2
c2
c1
c∩d => c1∩d1=K1, c2∩d2=K2
Точки 1 и 2 совпадают на П1 – горизонтально конкурирующие точки; 3 и 4 – фронтально конкурирующие точки (совпадают на П2)
Видимой считается точка, наиболее удаленная от оси x.
а)
б)
в)