Слайд 2Цели:
Повторить, обобщить, систематизировать и углубить знания о методах решения тригонометрических уравнений

Слайд 7Проекты
Применение тригонометрии в жизни
Тригонометрические уравнения при решение геометрических задач
Тригонометрические уравнения в заданиях

ЕГЭ
Графический способ решения тригонометрических уравнений с применением ПК
Слайд 9ПРИМЕНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ПРИ РЕШЕНИИ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ

Слайд 10Условие: В треугольнике из одной вершины проведены высота и медиана. Известно, что

угол разделился на три равные части. Определите углы треугольника.
Решение: Пусть в треугольнике АВС из вершины А проведены высота AH и медиана АМ. Каждый из трех равных углов при вершине А обозначим через х . К треугольникам АВМ и АМС (рис. 2) применим теорему синусов.
Слайд 12Тригонометрические уравнения
в заданиях ЕГЭ
Тригонометрический круг

Слайд 13Найти сумму всех целых значений параметра а, при которых уравнение
sin2x –

2cosx – 2 – a = 0
имеет решение.
Слайд 14Графический способ решения тригонометрических уравнений с применением ПК в программе MS Excel
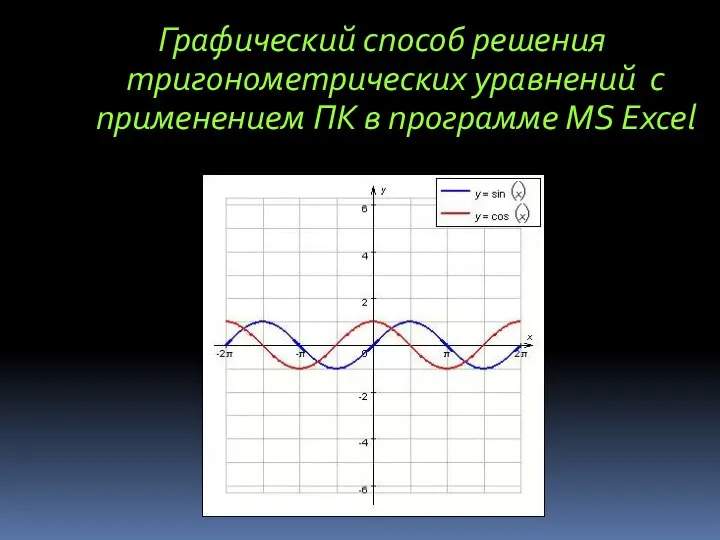
Слайд 15Применение тригонометрии в жизни

Слайд 16Происхождение названия
Слово «тригонометрия» впервые встречается в 1505г в заглавии книги немецкого теолога

и математика Питискуса. Происходит от греческих слов «треугольник» и «мера»,и это наука об измерении треугольников. Хотя название возникло относительно недавно, многие ее понятия и факты были известны уже две тысячи лет назад.
Слайд 17Древняя Греция
Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали

технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.
Слайд 18Как тригонометрия дошла до наших дней.
В 8 в. Учёные стран Ближнего и

Среднего Востока познакомились с трудами индийских математиков и астрономов и перевели их на арабский язык. В середине 9 века среднеазиатский учёный Аль-Хорезми написал сочинение «Об индийском счёте». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки.
Слайд 19Современная тригонометрия
Современный вид тригонометрии придал крупнейший математик восемнадцатого столетия Л. Эйлер. Он

ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. Различные факты стали доказываться путем применения формул, доказательства стали компактнее и проще.
Слайд 20Долгое время тригонометрия носила чисто геометрический характер. Такою она была еще в

средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Постепенно тригонометрия органически вошла в математический анализ, механику, физику и технические дисциплины.
Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались и приобрели важное значение для всей математики.
Слайд 21Применение в геодезии
Поскольку почти всякую фигуру можно разбить на множество треугольников, тригонометрия

дает мощный метод решения геометрических задач.
Чтобы воспользоваться им, строители туннелей намечают геодезический пункт, откуда видны концы туннеля. Затем они визируют направления и определяют углы между ними. Математический принцип предельно прост.
Слайд 22Применение в астрономии
На сфере, как и на поверхности Земли, о расстояниях можно

судить по углам под которыми они видны из центра сферы.
Положению точки на поверхности Земли определяются ее широтой (углом отсчитываемым от экватора) и долготой. Это дает мореплавателю расстояние и курсовой угол.
Астрономы определяют положение звезд при помощи таких сферических небесных треугольников.
Слайд 23Применение в технике
Применения тригонометрии разнообразны.
Принцип действия самозахватывающего ключа основан на измерении
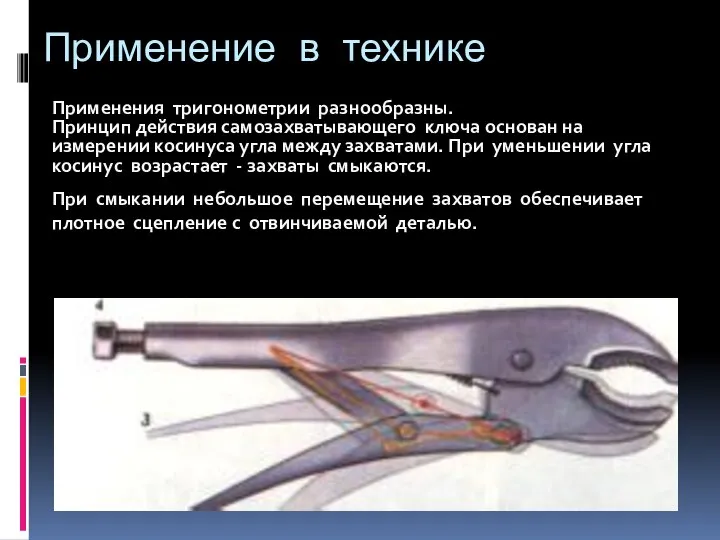
косинуса угла между захватами. При уменьшении угла косинус возрастает - захваты смыкаются.
При смыкании небольшое перемещение захватов обеспечивает плотное сцепление с отвинчиваемой деталью.
Слайд 24Применение в электротехнике
В технике и окружающем нас мире часто приходится сталкиваться с

периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными, например, колебания тока в электрической цепи. Колебательные явления различной физической природы подчиняются общим закономерностям, которые можно описать по закону синуса или косинуса.
Слайд 25Следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, анализ

финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика.
Слайд 26Тригонометрические уравнения одна из самых сложных тем в математике. Тригонометрические уравнения возникают

при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Тригонометрические уравнения и неравенства из года в год встречаются среди заданий ЕГЭ
Слайд 27Самостоятельная работа
«Выбор ответа»

Слайд 29Продолжи предложение
Сегодня я узнал…..
Было трудно…..
Я научился……………
Меня заинтересовало………….
Мне захотелось………
Меня удивило…………………
Теперь я могу………….





























 Размещение ЕДДС
Размещение ЕДДС Конная прогулка к Саблинскому водопаду
Конная прогулка к Саблинскому водопаду Сырный сервис
Сырный сервис Ювенальная юстиция в России
Ювенальная юстиция в России Площадь прямоугольника.
Площадь прямоугольника. Подготовительные недели Великого Поста
Подготовительные недели Великого Поста The Interview
The Interview  Открытое акционерное общество «Всероссийский научно-исследовательский и проектно- конструкторский институт атомного энергетиче
Открытое акционерное общество «Всероссийский научно-исследовательский и проектно- конструкторский институт атомного энергетиче Самостоятельность - фактор повышения образования
Самостоятельность - фактор повышения образования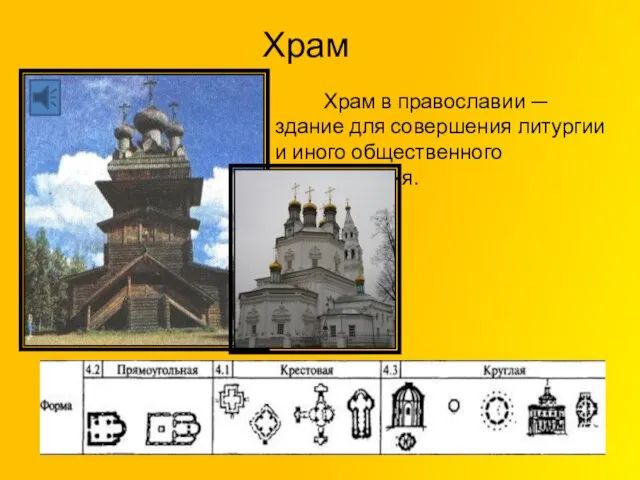 Храм
Храм You are what you eat
You are what you eat Минералы – свидетели эволюции органического мира на Земле
Минералы – свидетели эволюции органического мира на Земле Зрелый разум Результаты исследований по книге Gene Cohen “Mature mind” Гульнара Афрузовна Миннигалеева Кандидат пед.наук, доцент кафедры публичной политики Государственного университета «Высшая школа экономики» Председатель правления РОО КРЦП «Мои го
Зрелый разум Результаты исследований по книге Gene Cohen “Mature mind” Гульнара Афрузовна Миннигалеева Кандидат пед.наук, доцент кафедры публичной политики Государственного университета «Высшая школа экономики» Председатель правления РОО КРЦП «Мои го Родительское собрание 11 класса
Родительское собрание 11 класса Краткое описание учебной геологической карты(2 занятия)
Краткое описание учебной геологической карты(2 занятия) Исполнение бюджета города Братска за 2009 год
Исполнение бюджета города Братска за 2009 год Mobbing Стресс на работе. Психологический климат в коллективе
Mobbing Стресс на работе. Психологический климат в коллективе Информация о врачах
Информация о врачах Секция отечественной истории
Секция отечественной истории Теория Е и теория О организационных изменений
Теория Е и теория О организационных изменений Онлайн-курсы и индивидуальные занятия по спортивному ориентированию. Упражнение: Высота КП 2019 3 АN
Онлайн-курсы и индивидуальные занятия по спортивному ориентированию. Упражнение: Высота КП 2019 3 АN Дом в котором живем. Строительные конструкции, здания и сооружения
Дом в котором живем. Строительные конструкции, здания и сооружения Межнациональные отношения
Межнациональные отношения Berliner Luft
Berliner Luft Финансовые услуги
Финансовые услуги Презентация на тему Русская народная вышивка
Презентация на тему Русская народная вышивка Эмоционально-волевая сфера личности
Эмоционально-волевая сфера личности Projekt Aktywizacji Seniorów
Projekt Aktywizacji Seniorów