Слайд 3Множество:
множество четных чисел;
множество двузначных чисел;
множество правильных дробей со знаменателем 5;
множество диагоналей многоугольника;
множество

точек координатной плоскости;
множество прямых, проходящих через данную точку.
Слайд 4 Объекты или предметы, составляющие множество, называют элементами множества.
Например: число 89 – элемент

множества двузначных чисел.
Слайд 6 Множества бывают конечные и бесконечные.
Например: множество двузначных чисел – конечное множество (оно

содержит 90 элементов),
а множество четных чисел – бесконечное множество.
Слайд 9 Конечные множества обычно записывают с помощью фигурных скобок.
Например, множество вершин шестиугольника можно
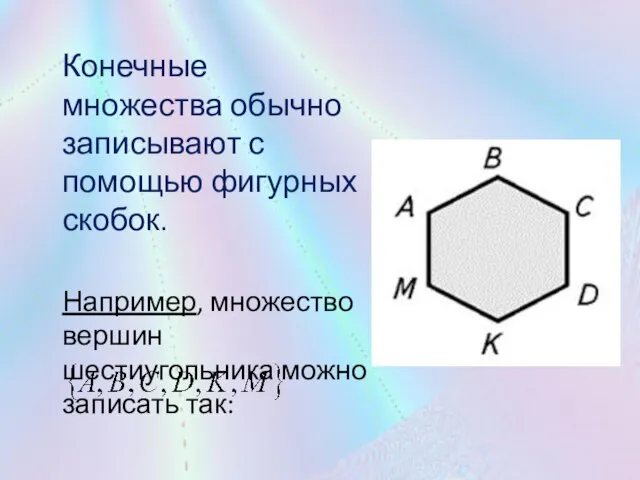
записать так:
Слайд 10 Множества принято обозначать большими буквами латинского алфавита.
Например, можно записать так

Слайд 11 Для основных числовых множеств введены специальные обозначения: множество натуральных чисел обозначают буквой

N (от латинского слова natural – «естественный», множество целых чисел – буквой Z (от немецкого слова zahl – «число», множество рациональных чисел – буквой Q (от латинского слова quotient – «отношение»).
Слайд 12 В тех случаях, когда задание множества перечислением элементов невозможно (как для бесконечного

множества) или громоздко (как для конечного множества с большим числом элементов), множество задают описанием, указав его характеристическое свойство, т.е. свойство, которым обладают все элементы этого множества и не обладают никакие другие объекты.











 Из истории квадратных уравнений
Из истории квадратных уравнений Световые приборы
Световые приборы НОВЫЕ ФОРМАТЫ ПОДРАЗДЕЛЕНИЙ СБЕРБАНКА РОССИИ
НОВЫЕ ФОРМАТЫ ПОДРАЗДЕЛЕНИЙ СБЕРБАНКА РОССИИ Брейн ринг. Интеллектуаль уен
Брейн ринг. Интеллектуаль уен Синтаксис сложного предложения (презентация к урокам в 5 классе)
Синтаксис сложного предложения (презентация к урокам в 5 классе) Презентация на тему Экологические сукцессии
Презентация на тему Экологические сукцессии  Масова частка елемента в речовині
Масова частка елемента в речовині KAZPROMAVTOMATIKA
KAZPROMAVTOMATIKA Конструирование юбки. Снятие мерок
Конструирование юбки. Снятие мерок НОУ ВПО «Волгоградский институт бизнеса» ЦЕНТР БЕСПЛАТНОЙ ЮРИДИЧЕСКОЙ ПОМОЩИ ЮРИДИЧЕСКАЯ КЛИНИКА ВОЛОНТЕРСКАЯ ОРГАНИЗАЦИЯ
НОУ ВПО «Волгоградский институт бизнеса» ЦЕНТР БЕСПЛАТНОЙ ЮРИДИЧЕСКОЙ ПОМОЩИ ЮРИДИЧЕСКАЯ КЛИНИКА ВОЛОНТЕРСКАЯ ОРГАНИЗАЦИЯ Презентация по физике.
Презентация по физике. Ачык дәресебез күңелле үтсен!
Ачык дәресебез күңелле үтсен! Парковки OnLine.
Парковки OnLine. Использование различных методов оценки стоимости собственного капитала в мире
Использование различных методов оценки стоимости собственного капитала в мире Железобетонные мосты
Железобетонные мосты  Апаратты кодтау жне сатау СРС
Апаратты кодтау жне сатау СРС Адаптация к школе
Адаптация к школе Пионербол
Пионербол Сборный портфель – одна из форм учета учебных достижений первоклассников в условиях безотметочного обучения
Сборный портфель – одна из форм учета учебных достижений первоклассников в условиях безотметочного обучения ЧеловеческиеРасы
ЧеловеческиеРасы Содержание витамина С (аскорбиновой кислоты) в натуральных и консервированных соках
Содержание витамина С (аскорбиновой кислоты) в натуральных и консервированных соках Фронтир
Фронтир Ливневые канализации
Ливневые канализации Псалом 20. Новая святорусская редакция
Псалом 20. Новая святорусская редакция Завершение сделки. Процесс оказания помощи клиенту в принятии решения
Завершение сделки. Процесс оказания помощи клиенту в принятии решения Школьный двор
Школьный двор Информационный таргетинг
Информационный таргетинг Основные технические характеристики очередей
Основные технические характеристики очередей