Модели атомных ядер

Модели атомных ядер.
Что мы ждём?
Микроскопические и коллективные модели.
Модель жидкой капли.
Оболочечная модель.
Модель Ферми-газа.
Оптическая модель.

Что мы ждём?
Стабильность ядер?
Виды распадов?
Энергии и угловые распределения частиц?
Радиусы, массы, энергии связи?
Спины, моменты, чётности?
Энергетические уровни?
Вероятности переходов?
Сечения взаимодействия?
Распространённость изотопов?
.............

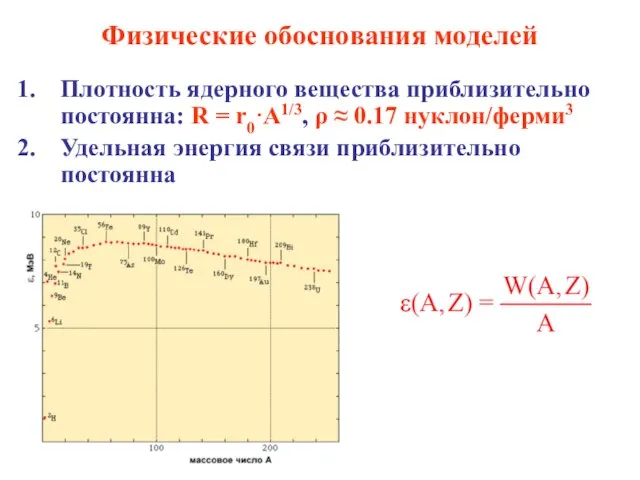
Физические обоснования моделей
Плотность ядерного вещества приблизительно постоянна: R = r0·A1/3, ρ ≈ 0.17 нуклон/ферми3
Удельная энергия связи приблизительно постоянна

Свойства 1 и 2 обусловлены природой ядерных сил, которые имеют конечный радиус действия и вызывают сильное взаимное притяжение нуклонов, находящихся друг от друга на расстоянии от ~2 ферми до ~0.5 ферми, но при уменьшении этого расстояния начинают действовать как очень сильные отталкивающие силы.

Коллективные модели
в этих моделях предполагается, что взаимодействие между соседними нуклонами настолько велико, что степени свободы индивидуальных нуклонов можно не учитывать
(капельная модель, макроскопические модели).

Физические обоснования моделей
Средняя длина пробега нуклонов в ядре велика по сравнению с расстоянием между ними и превышает размеры ядра. Взаимодействие нуклонов приводит к возникновению среднего ядерного поля, в котором частицы движутся независимо друг от друга.
(модели независимых частиц, микроскопические модели)

Капельная модель
Опыты Резерфорда по изучению α-радиоактивности 1911 год.
R = r0·A1/3,
ρn = A/V = A/(4/3πR3) ≈ 1038 нуклон/cм3,
ρ(г/см3) = ρnmn ≈ 1014 г/см3

1934: поиск трансуранов
238U + n → 239U* → 239Nn + e− + ν
92
92
93
Otto Hahn und Lise Meitner
−
−
−
+
+
+

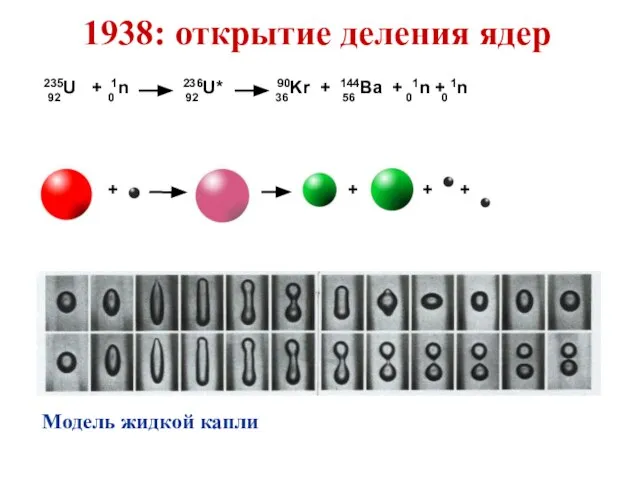
1938: открытие деления ядер
235U + 1n 236U* 90Kr + 144Ba + 1n + 1n
92 0 92 36 56 0 0
Модель жидкой капли
+
+
+
+

Формула Вайцзеккера
Энергия связи ядра W(A,Z) – энергия, которая необходима для того, чтобы разделить ядро на отдельные составляющие его нуклоны. W ≈ αA
Нуклоны неравноценны
W ≈ αA – βА2/3
Кулоновское расталкивание
W ≈ αA - βА2/3- γZ2/A1/3

«Некапельные» члены
«Энергия симметрии»
- δ (A/2 – Z)2/A
Эффекты чётности
ζA-3/4

Формула Вайцзеккера

Область применения
Вычисление энергии связи с точностью ~10-4
Вычисление масс ядер;
Вычисление энергий отделения частиц;
Вычисление энергий распадов;
Колебания жидкости;
Качественная теория деления ядер;
Линия β-стабильности.

Недостатки
Непоследовательность модели;
Низкая точность;
Качественный характер;
Игнорирует периодичность.

Модель ферми-газа
В этой модели рассматривается движение невзаимодействующих друг с другом нуклонов в области объемом V, в пределах которой потенциал считается постоянным,
Волновые функции нуклонов – плоские волны,
В ограниченном объеме V возможен только дискретный набор значений вектора импульса,
На каждом нейтронном (или протонном) уровне могут в соответствии с принципом Паули находится только два нейтрона (или протона), имеющие разные проекции спина,
Граница, разделяющая заполненные и незаполненные одночастичные уровни, называется границей Ферми.

Из статистики Ферми:

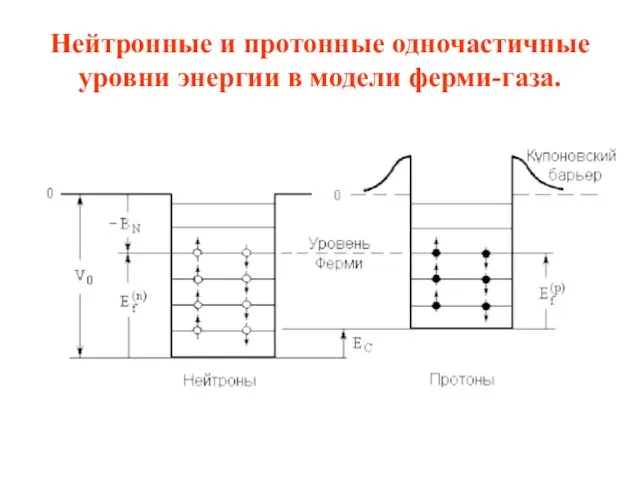
Нейтронные и протонные одночастичные уровни энергии в модели ферми-газа.

Область применения
В случаях, где важно движение нуклонов внутри ядра: рождение частиц, некоторые реакции.

Оболочечная модель
В модели оболочек предполагается, что нуклоны движутся независимо друг от друга в сферически-симметричной потенциальной яме. Собственные состояния нуклона в такой яме находят, решая соответствующее уравнение Шредингера.

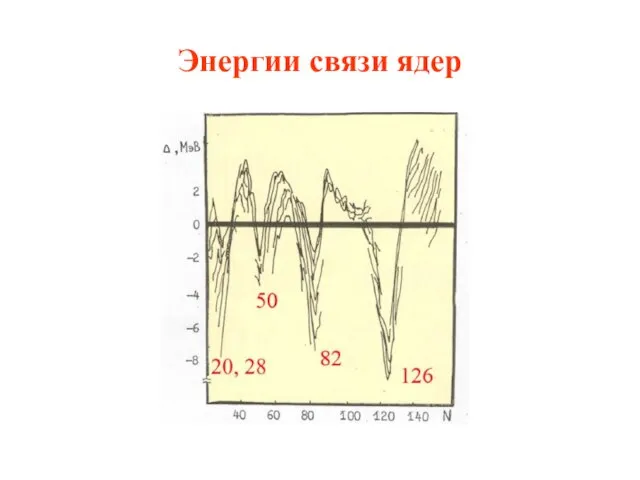
Обоснование модели
Периодичность свойств;
Магические числа: 2, 8, 20, 50, 82, 126;
Нулевые квадрупольные моменты (сферичность ядер);
Распространённость изотопов.

Энергии связи ядер

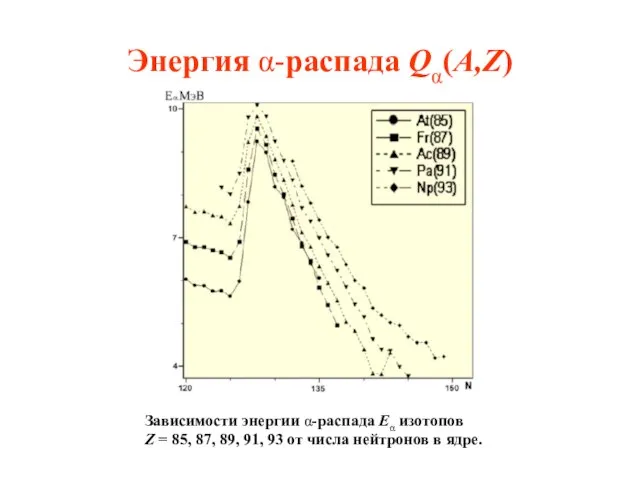
Энергия α-распада Qα(A,Z)
Зависимости энергии α-распада Eα изотопов
Z = 85, 87, 89, 91, 93 от числа нейтронов в ядре.

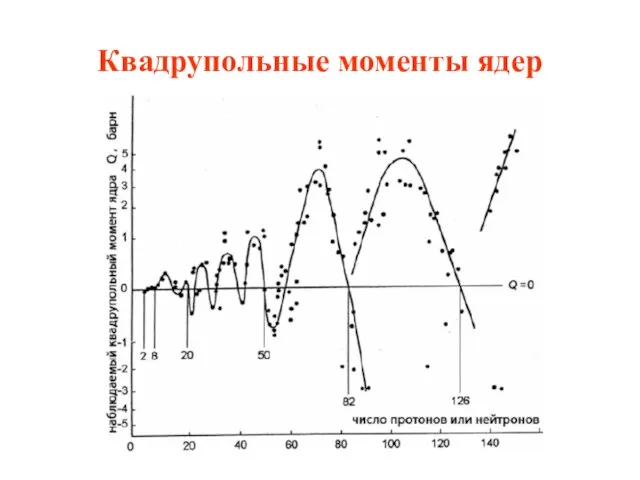
Квадрупольные моменты ядер

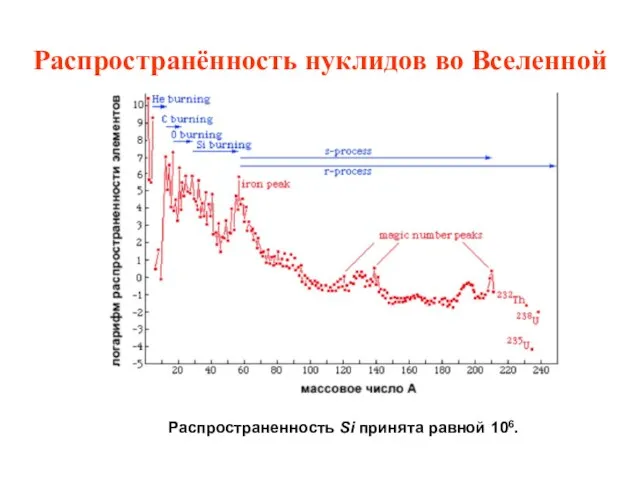
Распространённость нуклидов во Вселенной
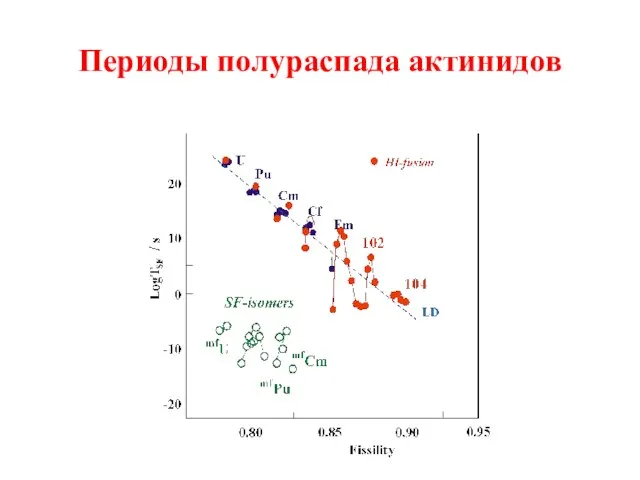
Распространенность Si принята равной 106.

Периоды полураспада актинидов

Первые попытки: Бартлет (1932 г.) и Эльзассер (1933 г.): объяснили 2, 8, 20.
Окончательный вид 1949 г: М. Гепперт-Майер и Дж. Иенсен.

Построение модели
Принцип Паули выполняется.
В атоме есть силовой центр и электроны слабо взаимодействуют между собой.
В ядре нет силового центра, нуклоны сильно взаимодействуют между собой.
n ≈ 1038 нукл/см3; σ ≈ 3·10-25 см2;
λ = 1/(nσ) ≈ 3·10-14см !!

Построение модели
Малый радиус взаимодействия.
Сложение эффектов от потенциальных ям.
Большая плотность ядра → однородность потенциала.
Принцип Паули → большая длина свободного пробега → отсутствие взаимодействия.

Основные положения:
В сферическом потенциале движутся невзаимодействующие нуклоны.
Потенциал одинаков для протонов и нейтронов.
Орбитальный момент является интегралом движения.
Выполняется принцип Паули (2(2l+1)).
Решения уравнений Шредингера.

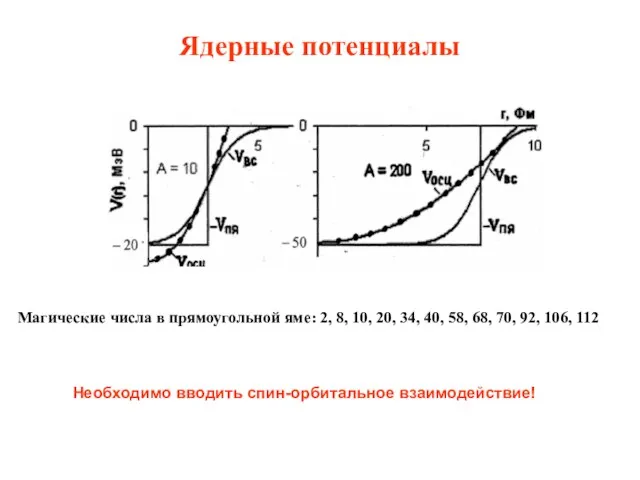
Ядерные потенциалы
В первом приближении можно считать ядерный потенциал сферически
симметричным. В качестве потенциалов используют:

Ядерные потенциалы
Магические числа в прямоугольной яме: 2, 8, 10, 20, 34, 40, 58, 68, 70, 92, 106, 112
Необходимо вводить спин-орбитальное взаимодействие!

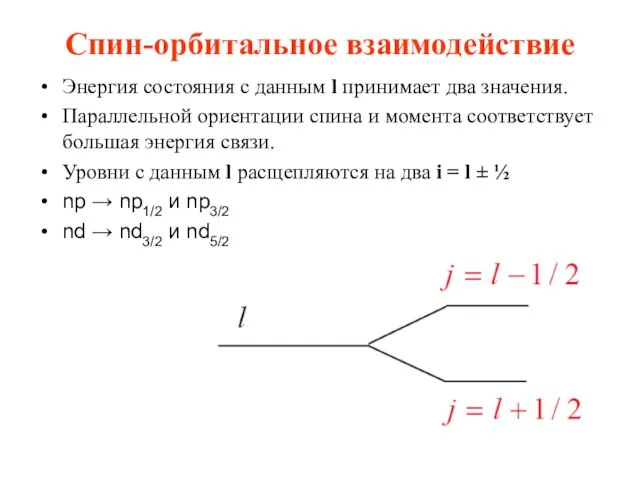
Спин-орбитальное взаимодействие
Энергия состояния с данным l принимает два значения.
Параллельной ориентации спина и момента соответствует большая энергия связи.
Уровни с данным l расщепляются на два i = l ± ½
np → np1/2 и np3/2
nd → nd3/2 и nd5/2

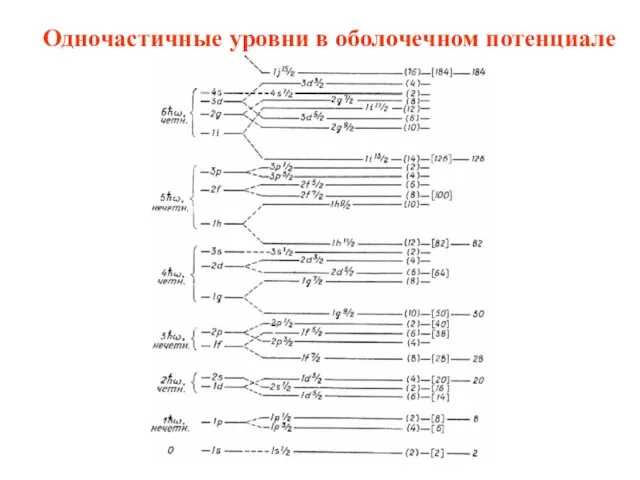
Одночастичные уровни в оболочечном потенциале

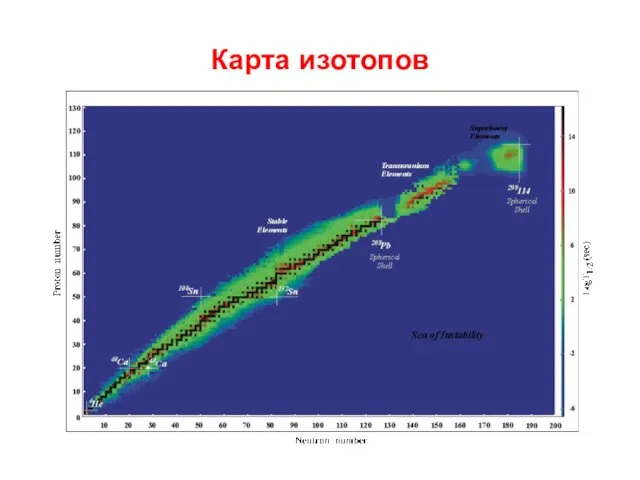
Карта изотопов

Недостатки оболочечной модели
Объясняет немногие свойства ядер в основном состоянии.
Неправильные значения спинов.
Наличие вращательных уровней у чётно-чётных ядер.
Заниженные значения электрических квадрупольных моментов.
Заниженные вероятности Е2 переходов.

Недостатки оболочечной модели
Объясняет немногие свойства ядер в основном состоянии.
Неправильные значения спинов.
Наличие вращательных уровней у чётно-чётных ядер.
Заниженные значения электрических квадрупольных моментов.
Заниженные вероятности Е2 переходов.

Обобщённая модель ядра
Потенциал не является жёстким.
Взаимодействие определяется числом нуклонов сверх замкнутой оболочки.
Центробежное давление на стенки ядра.
Деформация ядер в основном состоянии.
Появление вращательных степеней свободы.
Перестройка остова ядра.
Связь всех степеней свободы.

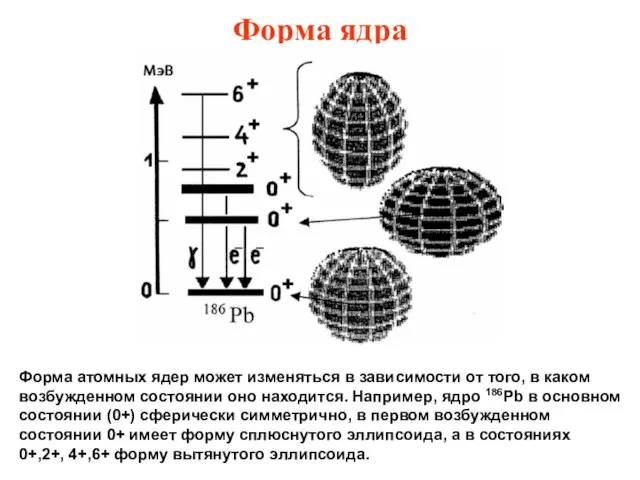
Форма ядра
Форма атомных ядер может изменяться в зависимости от того, в каком
возбужденном состоянии оно находится. Например, ядро 186Pb в основном
состоянии (0+) сферически симметрично, в первом возбужденном
состоянии 0+ имеет форму сплюснутого эллипсоида, а в состояниях
0+,2+, 4+,6+ форму вытянутого эллипсоида.

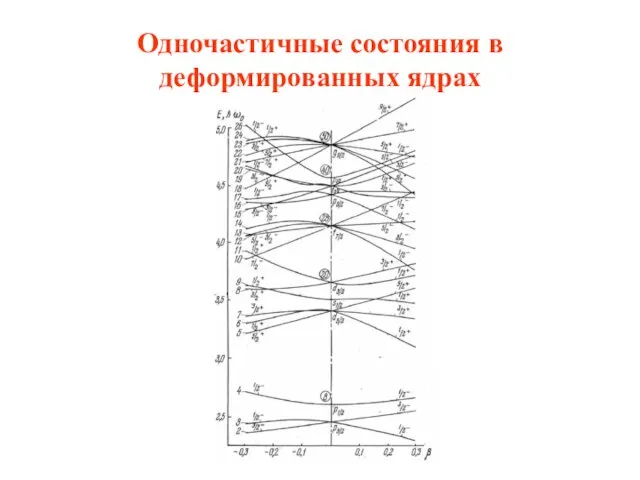
Одночастичные состояния в деформированных ядрах
Аксиально-симметричный потенциал гармонического осциллятора – потенциал Нильссона.
Положение одночастичных уровней в потенциале Нильссона зависит от величины и знака параметра деформации β.

В сферически-симметричной потенциальной яме состояния нуклона характеризуются квантовыми числами орбитального l и полного моментов j =l ±½ , причем уровни вырождены по проекции момента j на ось z, т.е. кратность вырождения равна 2j + 1.
В деформированном ядре состояния нуклона нельзя характеризовать квантовыми числами l и j. Однако так как сохраняется симметрия относительно поворотов вокруг оси z (аксиальная симметрия), то момент количества движения, создаваемый нуклоном, характеризуют квантовым числом K проекции момента j на ось симметрии z.

Одночастичные состояния в деформированных ядрах

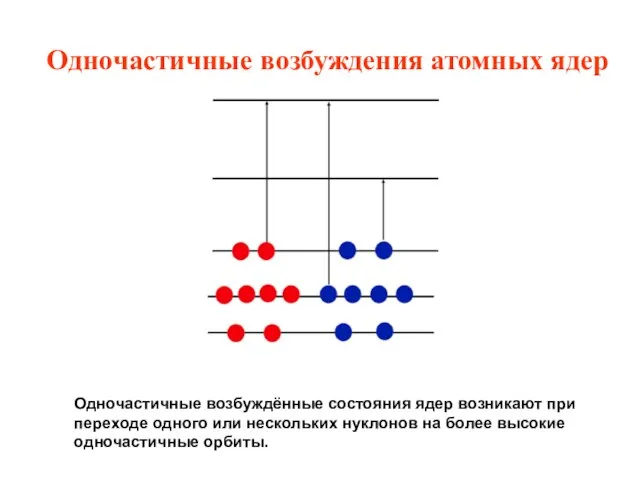
Одночастичные возбуждения атомных ядер
Одночастичные возбуждённые состояния ядер возникают при
переходе одного или нескольких нуклонов на более высокие
одночастичные орбиты.

Вращательные состояния ядер
Сферически-симметричное ядро не может иметь вращательной энергии.
Если равновесная форма ядра не сферична (деформирована), то появляется пространственная анизотропия, а вместе с ней и вращательные степени свободы.
Такое ядро обязательно имеет внутренний электрический квадрупольный момент Q0.

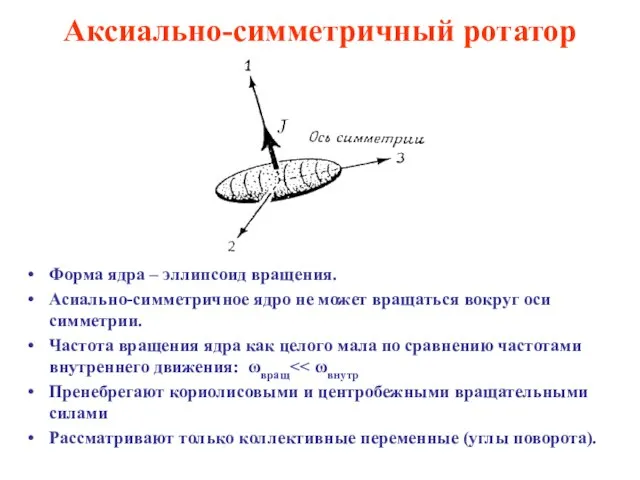
Аксиально-симметричный ротатор
Форма ядра – эллипсоид вращения.
Асиально-симметричное ядро не может вращаться вокруг оси симметрии.
Частота вращения ядра как целого мала по сравнению частотами внутреннего движения: ωвращ<< ωвнутр
Пренебрегают кориолисовыми и центробежными вращательными силами
Рассматривают только коллективные переменные (углы поворота).

Сложение моментов
Полный момент количества движения ядра складывается из коллективного вращательного момента ядра и внутреннего момента нуклонов
I = K + Ω
Eвращ= Ω2/2Jэфф= (I2 – K2)/2Jэфф= ħ2/2Jэфф[I(I+1)-K(K+1)]
При К=0: Eвращ= ħ2 I(I+1) /2Jэфф, I=0, 2, 4, 6
Jэфф=J0(ΔR/R)2

Энергетические уровни 168Er

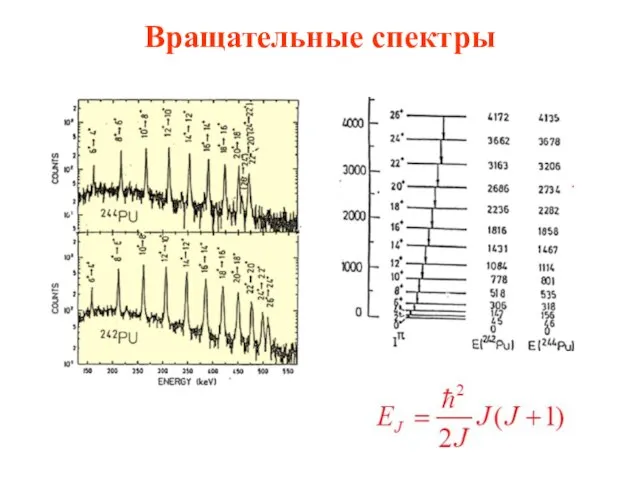
Вращательные спектры

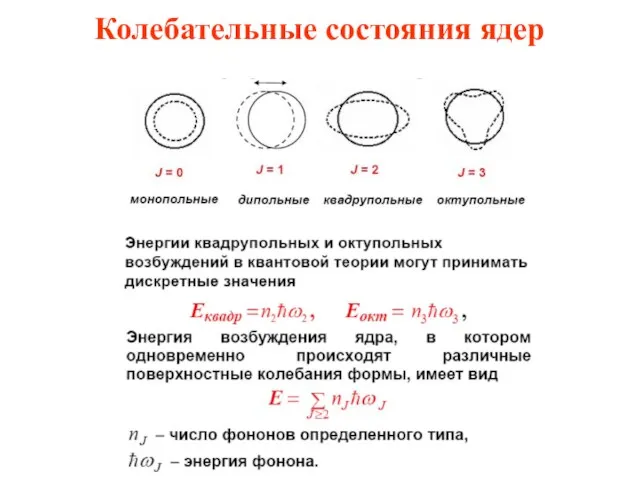
Колебательные состояния ядер

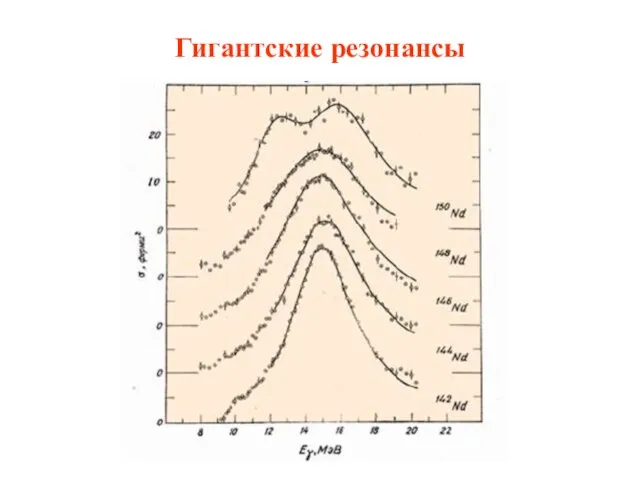
Гигантские резонансы