Муниципальное нетиповое общеобразовательное учреждение «Лицей» Учебный проект «Применение математических функций в жизни чел
Содержание
- 2. Введение Мы поставили перед собой задачу выявить и изучить области, в которых применяется функция и её
- 3. История развития понятия функции с древнейших времён до 17 века - задание функции: площадь круга является
- 4. Франсуа Виет (1540 – 1603гг.) История развития понятия функции в 17 веке Рене Декарт (1596-1650гг.) Пьер
- 5. Декарт Рене, Франсуа Виет Декарт Рене, Ферма Пьер Декарт Рене - понятие функции представление кривые в
- 6. Готфрид Вильгельм фон Лейбниц Функция (от лат. Functio – совершение, выполнение) – отрезок, длина которого меняется
- 7. Основные понятия: применил знак для х- (х) - Впервые сделал подход к аналитической функции Иоганн Бернули
- 8. Основные понятия: Сформулировал общее определение понятия функции. Примером является функция Дирихле Дирихле Петер Густав Лежён Функция
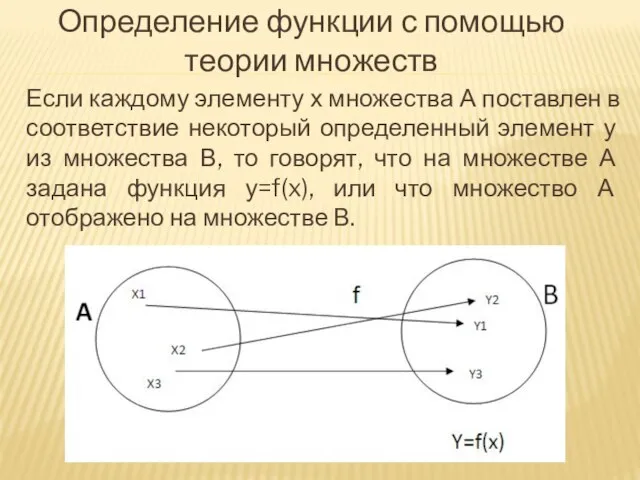
- 9. Определение функции с помощью теории множеств Если каждому элементу х множества А поставлен в соответствие некоторый
- 10. Определение функции в школьной программе 7 класс Линейная функция: , 8 класс Квадратичная функция: , 9
- 11. Применение функций в точных науках Физика Астрономия Звук Графики зависимости физических величин, Звёздный график, Параболоиды, Отображение
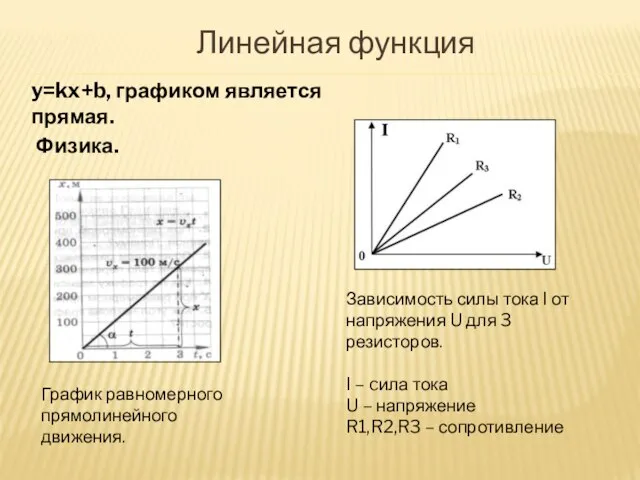
- 12. Линейная функция График равномерного прямолинейного движения. Физика. Зависимость силы тока I от напряжения U для 3
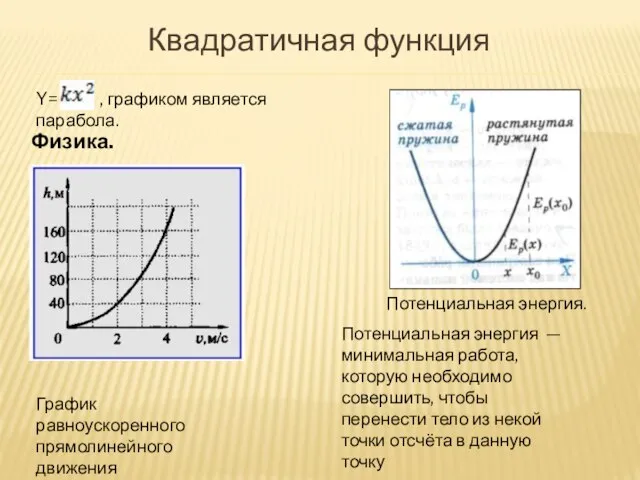
- 13. Квадратичная функция График равноускоренного прямолинейного движения Физика. Потенциальная энергия. Потенциальная энергия — минимальная работа, которую необходимо
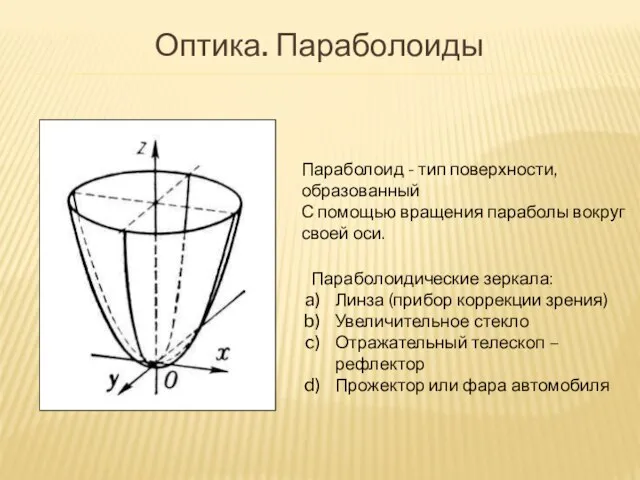
- 14. Параболоидические зеркала: Линза (прибор коррекции зрения) Увеличительное стекло Отражательный телескоп – рефлектор Прожектор или фара автомобиля
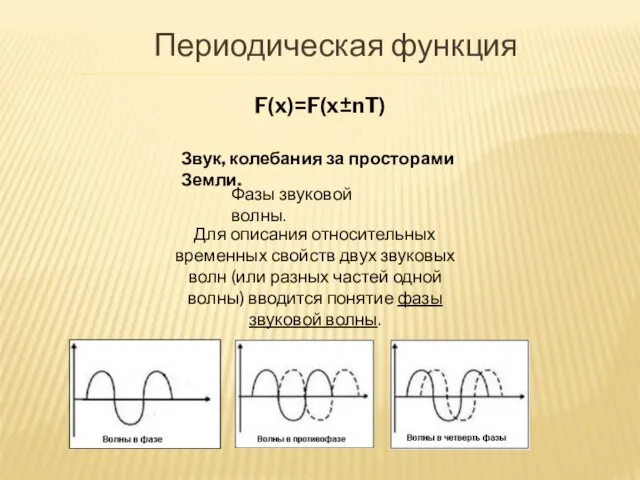
- 15. Периодическая функция Звук, колебания за просторами Земли. Для описания относительных временных свойств двух звуковых волн (или
- 16. Логарифмическая функция и равносильны. Записи
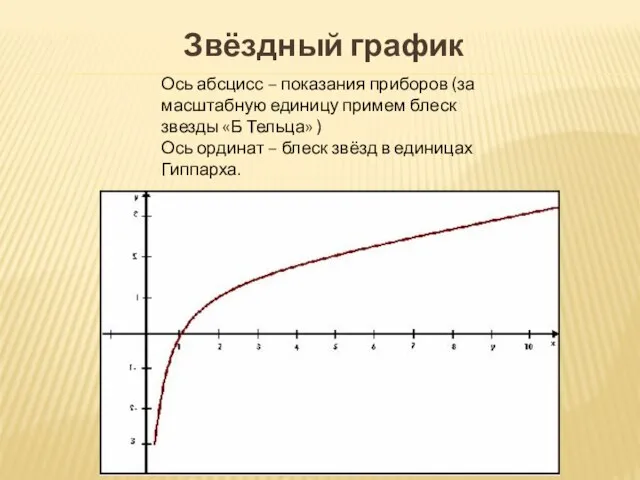
- 17. Ось абсцисс – показания приборов (за масштабную единицу примем блеск звезды «Б Тельца» ) Ось ординат
- 18. ПРИМЕНЕНИЕ ФУНКЦИИ В ЕСТЕСТВЕННЫХ НАУКАХ
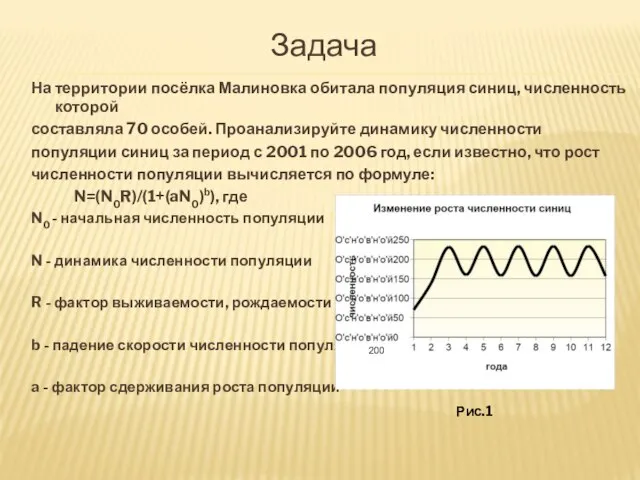
- 19. Задача На территории посёлка Малиновка обитала популяция синиц, численность которой составляла 70 особей. Проанализируйте динамику численности
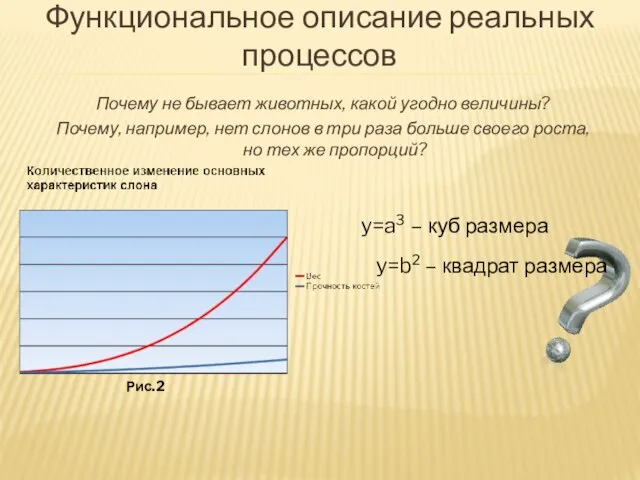
- 20. Функциональное описание реальных процессов Почему не бывает животных, какой угодно величины? Почему, например, нет слонов в
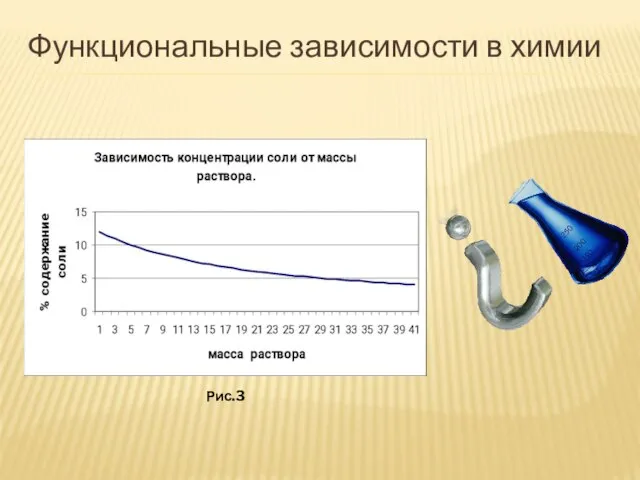
- 21. Функциональные зависимости в химии Рис.3
- 22. Применение в биологии и химии показательной функции Показательной функцией называется функция вида у = ax, где
- 23. ПРИМЕНЕНИЕ ФУНКЦИИ В ИСТОРИИ И ФИЛОЛОГИИ
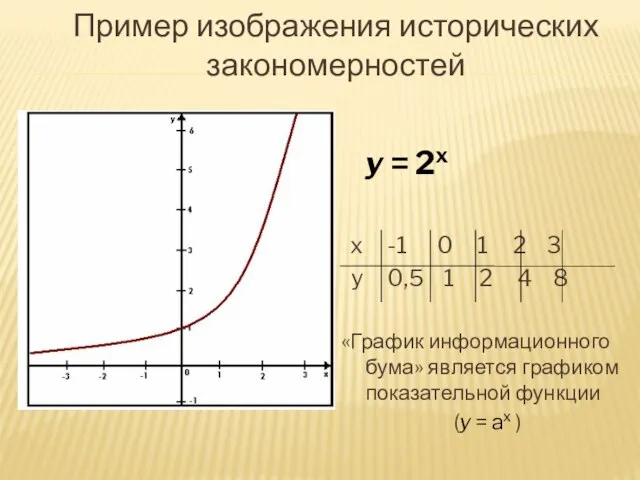
- 24. Пример изображения исторических закономерностей y = 2x x -1 0 1 2 3 y 0,5 1
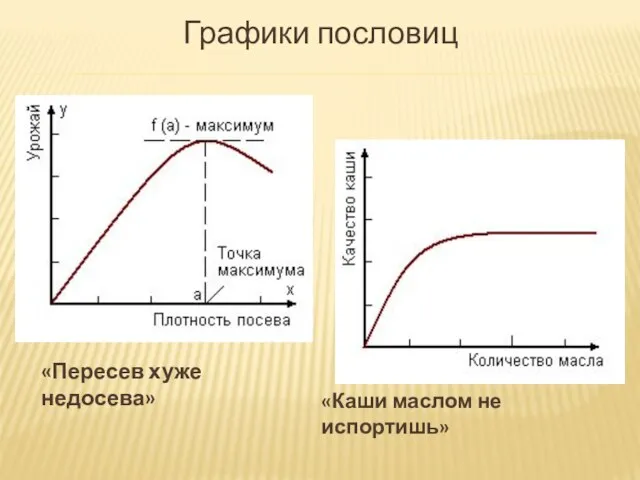
- 25. Графики пословиц «Каши маслом не испортишь» «Пересев хуже недосева»
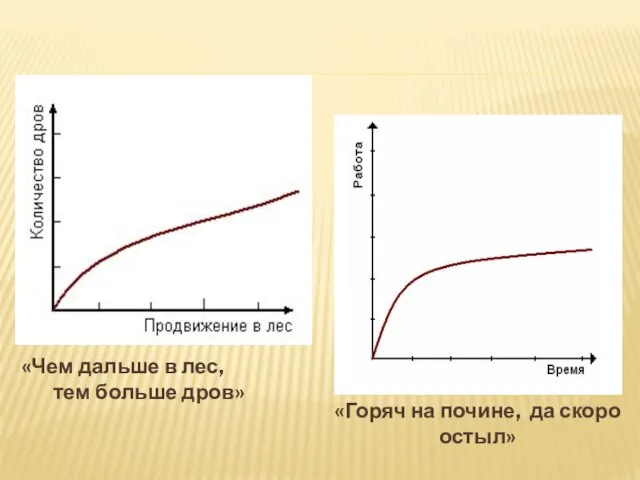
- 26. «Чем дальше в лес, тем больше дров» «Горяч на почине, да скоро остыл»
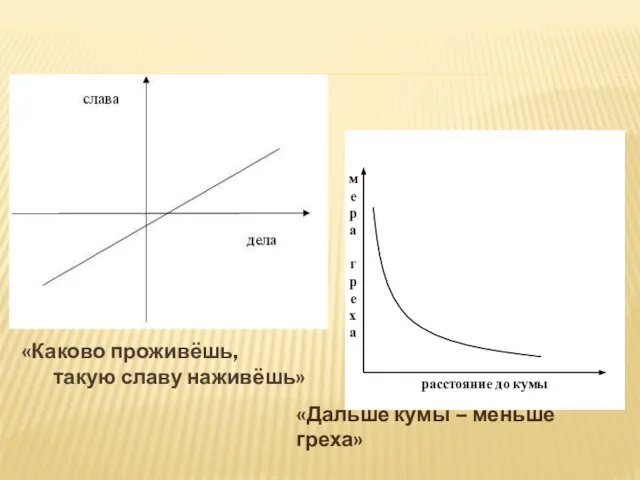
- 27. «Каково проживёшь, такую славу наживёшь» расстояние до кумы м е р а г р е х
- 28. ПРИМЕНЕНИЕ ФУНКЦИИ В ЖИЗНИ
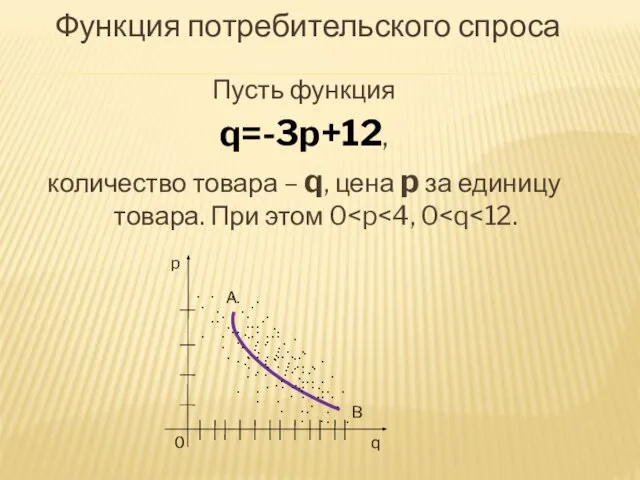
- 29. Функция потребительского спроса Пусть функция q=-3p+12, количество товара – q, цена p за единицу товара. При
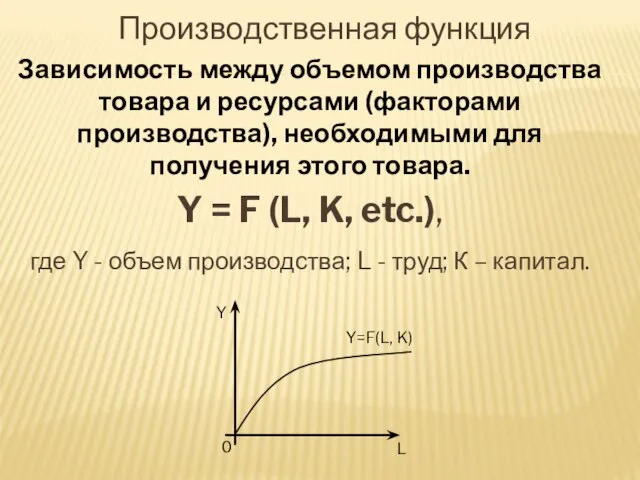
- 30. Производственная функция Зависимость между объемом производства товара и ресурсами (факторами производства), необходимыми для получения этого товара.
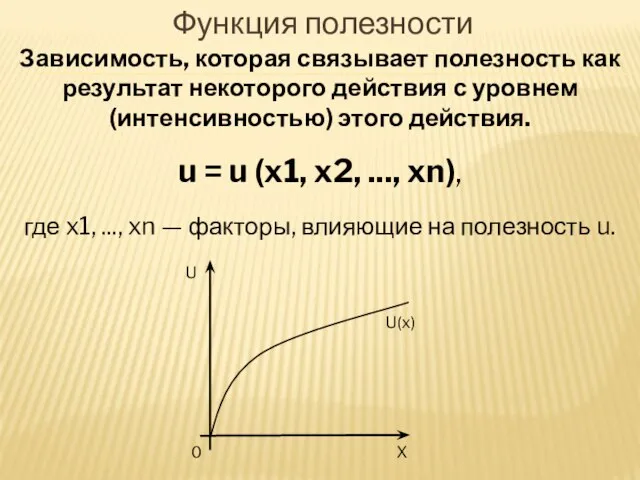
- 31. Функция полезности Зависимость, которая связывает полезность как результат некоторого действия с уровнем (интенсивностью) этого действия. u
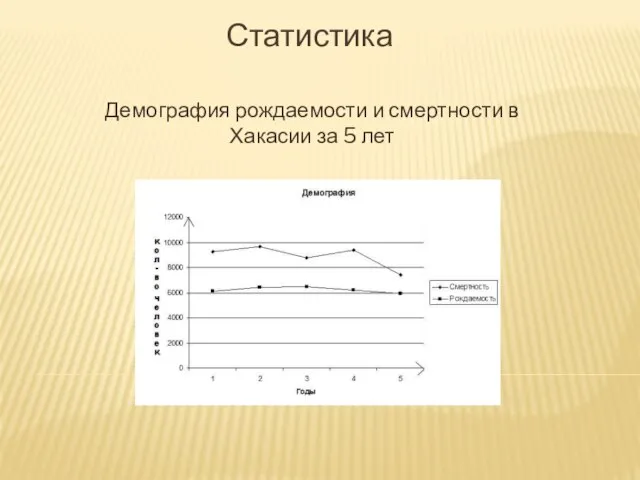
- 32. Статистика Демография рождаемости и смертности в Хакасии за 5 лет
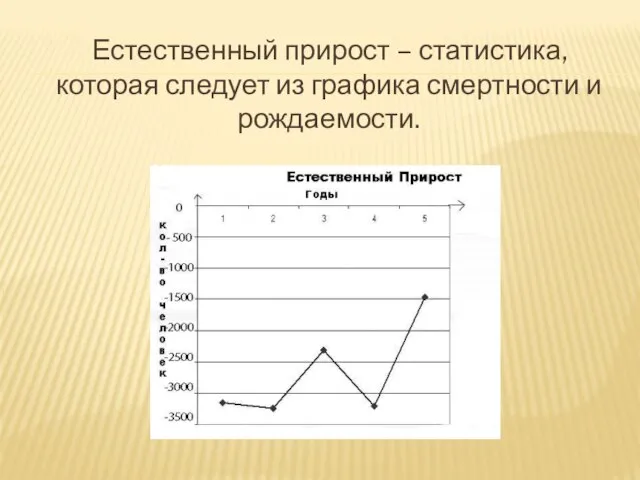
- 33. Естественный прирост – статистика, которая следует из графика смертности и рождаемости.
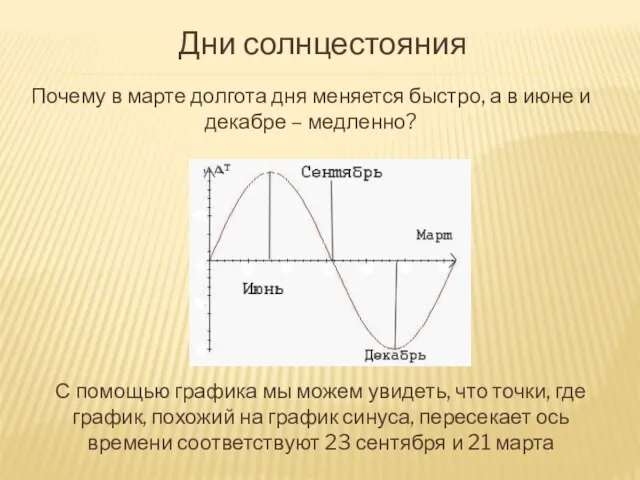
- 34. Дни солнцестояния Почему в марте долгота дня меняется быстро, а в июне и декабре – медленно?
- 35. Задача №1 Человек кидает мяч. Какую скорость, траекторию он ему сообщает? Ответ: Множество траекторий полёта в
- 36. Задача №2 Какую траекторию полёта имеют космические тела и почему? Ответ: Траектория в форме параболы. Потому
- 37. Задача №3 Какую форму принимает поверхность жидкости при вращении тонкого прямоугольного сосуда вокруг своей вертикальной оси?
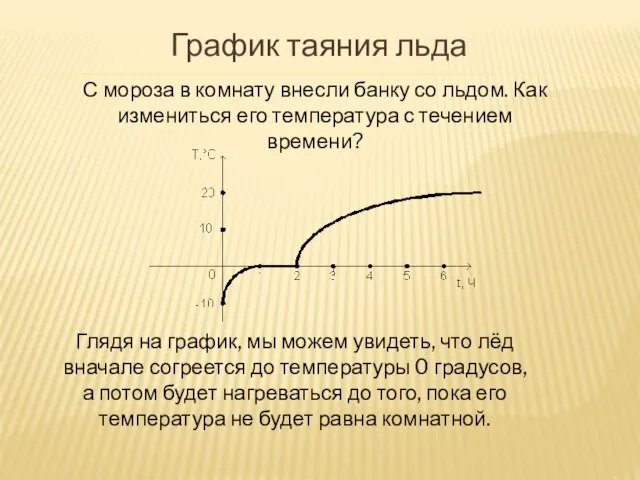
- 38. С мороза в комнату внесли банку со льдом. Как измениться его температура с течением времени? Глядя
- 39. Таблица стоимости проезда Представлена таблица стоимости проезда в пригородном транспорте, где n – номер зоны; m
- 40. Заключение Подведём итоги всего вышесказанного. Мы рассмотрели основные области применения функции и её свойства. Мы надеемся,
- 42. Скачать презентацию


















 Lluvia
Lluvia Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах
Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах УД ПСИХОЛОГИЯ
УД ПСИХОЛОГИЯ Храмы России
Храмы России Оптическая микроскопия
Оптическая микроскопия Менеджмент
Менеджмент Кондитерский отдел
Кондитерский отдел Органы и службы стандартизации РФ
Органы и службы стандартизации РФ Вышел зайчик погулять Художник – В. Сергеев
Вышел зайчик погулять Художник – В. Сергеев Знакомство с точкой
Знакомство с точкой Состояние и задачи управления проектами в строительстве
Состояние и задачи управления проектами в строительстве Торцевой разрез. Материаловедение
Торцевой разрез. Материаловедение чайные истории
чайные истории Шпаргалка юного покупателя
Шпаргалка юного покупателя Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор
Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор Классификация реакций
Классификация реакций Организация хранения документов Архивного фонда Российской Федерации и других архивных документов
Организация хранения документов Архивного фонда Российской Федерации и других архивных документов Трансляция – биосинтез белка на рибосоме
Трансляция – биосинтез белка на рибосоме Инновационный подход к жизни
Инновационный подход к жизни DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D
DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D Урок – размышление по рассказу К.Г. Паустовского «Телеграмма»
Урок – размышление по рассказу К.Г. Паустовского «Телеграмма» Путешествие в мир животных
Путешествие в мир животных СПАСИБО, АЗБУКА!
СПАСИБО, АЗБУКА! Rave Cosmology Today Dying, Death & Bardo . RC3.8
Rave Cosmology Today Dying, Death & Bardo . RC3.8 Основные закономерности развития информационного пространства
Основные закономерности развития информационного пространства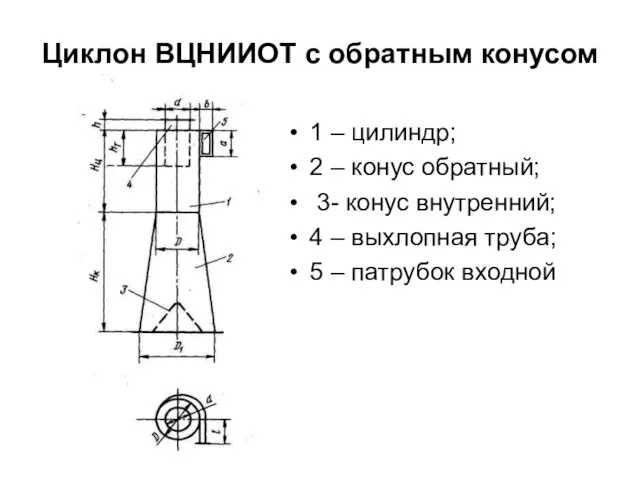 Циклон ВЦНИИОТ с обратным конусом
Циклон ВЦНИИОТ с обратным конусом  Квантовые компьютеры
Квантовые компьютеры Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)
Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)