Начертательная геометрия. Плоскость. Главные линии плоскости

ПЛОСКОСТЬ
Задание и изображение на чертеже
Положение плоскости в пространстве и на чертеже можно определить:
1) тремя точками, не лежащими на одной прямой;
2) прямой и точкой вне ее;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми;
5) любой плоской фигурой;
6) следами.
Следом плоскости называется линия пересечения этой плоскости с плоскостями проекций. Горизонтальный след PП1; фронтальный PП2
Плоскость, не перпендикулярная ни одной плоскости проекций, называется плоскостью общего положения. На комплексном чертеже проекции элементов, задающих плоскость, занимают общее положение.
Плоскость, перпендикулярная или параллельная одной из плоскостей проекций, называется плоскостью частного положения.
1)
2)
3)
4)
5)
6).
Px
PП2
PП1

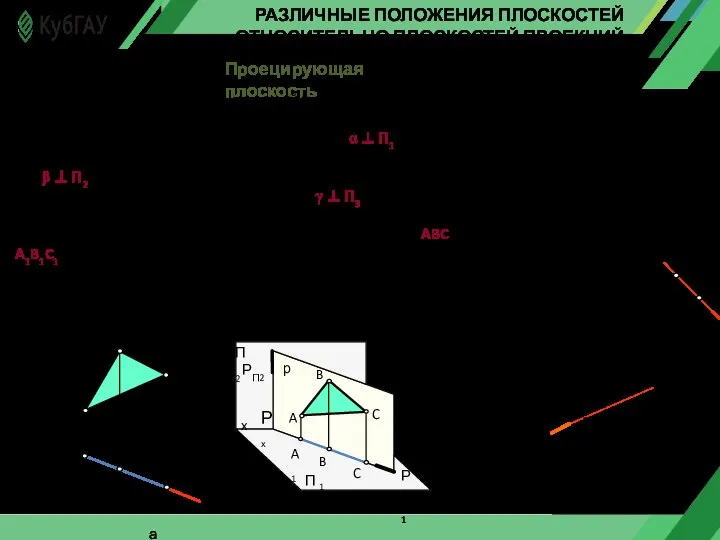
РАЗЛИЧНЫЕ ПОЛОЖЕНИЯ ПЛОСКОСТЕЙ
ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Проецирующая плоскость
Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей. Различают:
горизонтально проецирующая плоскость (α ⊥ П1 ); б) фронтально проецирующая плоскость
(β ⊥ П2);
в) профильно-проецирующая плоскость (γ ⊥ П3).
У проецирующих плоскостей одна проекция вырождается в прямую. Поэтому проекция фигуры, принадлежащей такой плоскости (треугольник ABC), вырождается в прямую (A1B1C1). Проецирующая плоскость однозначно задается на чертеже своей линейной проекцией или проецирующим следом плоскости( Рп1 Рп2 Рп3)
ψ
ϕ
λ
x
x
z
x
а)
б)
в)
РП1
РП2
Рх

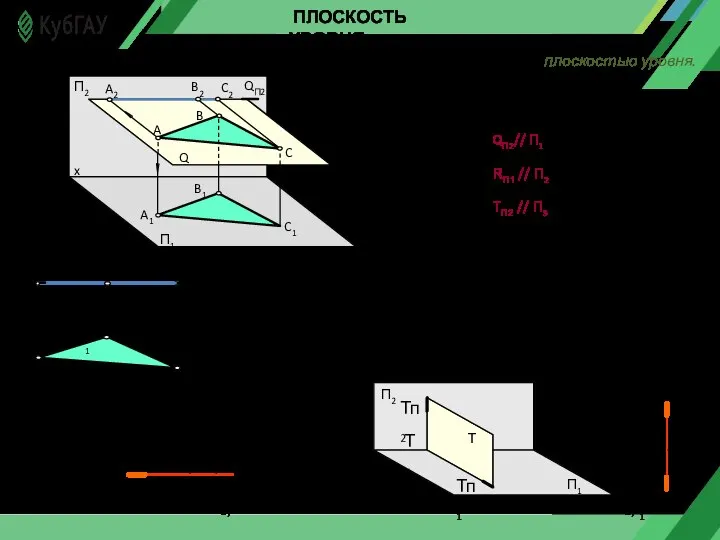
ПЛОСКОСТЬ УРОВНЯ
Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.
Различают:
а) горизонтальная плоскость
уровня (QП2// П1);
б) фронтальная плоскость
уровня (RП1 // П2);
в) профильная плоскость
уровня (TП2 // П3).
Плоскость уровня является част-
ным случаем проецирующей
плоскости, поэтому на чертеже
задается своей линейной проек-
цией или собирательным следом
Фигура, принадлежащая плоскости
уровня, проецируется на соответ-
ствующую плоскость проекций в
натуральную величину.
x
x
Т
П2
П1
а)
б)
в)
A
B
C
П1
П2
x
Тх
а1≡b1≡ Rп1
Тп1
Тх
Тп2
Тп2
Тп1

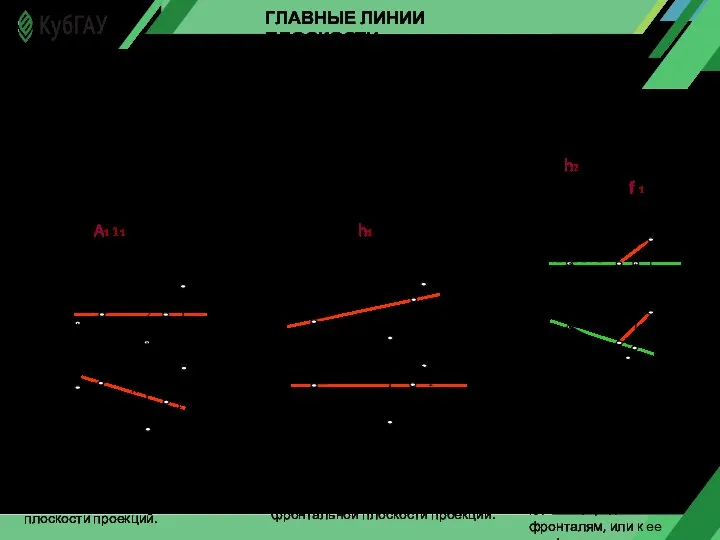
ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
В любой плоскости можно провести бесчисленное множество главных линий: а) горизонтали; б) фронтали; в) профильные прямые; г) линии наибольшего ската. Линии наибольшего ската - прямые, проведенные в плоскости перпендикулярно к горизонталям этой плоскости.
Построение горизонтали начинают с ее фронтальной проекции h2; построение фронтали плоскости начинают с ее горизонтальной проекции f 1; линию ската начинают с ее горизонтальной
проекции A1 11, которая перпендикулярна h1.
Поэтапное построение горизонтали, фронтали и линии наибольшего
ската показано на следующем слайде.
а)
б)
в)
1
21
С
2
2
1
1
1
Горизонталью называется прямая лежащая в плоскости и параллельная горизонтальной плоскости проекций.
Фронталью называется прямая принадлежащая заданной плоскости и параллельная фронтальной плоскости проекций.
Линиями наибольшего наклона плоскости к плоскостям П1, П2 и П3 называют прямые, лежащие в ней и перпендикулярные или к горизонтальной плоскости, или к ее фронталям, или к ее профильным прямым.

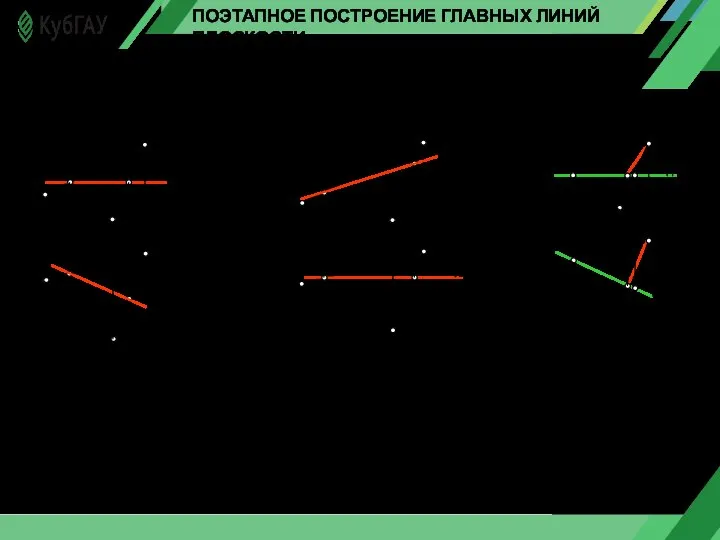
ПОЭТАПНОЕ ПОСТРОЕНИЕ ГЛАВНЫХ ЛИНИЙ ПЛОСКОСТИ
а)
б)
г)
2
С
2
1
1
1
1
1
С
С2

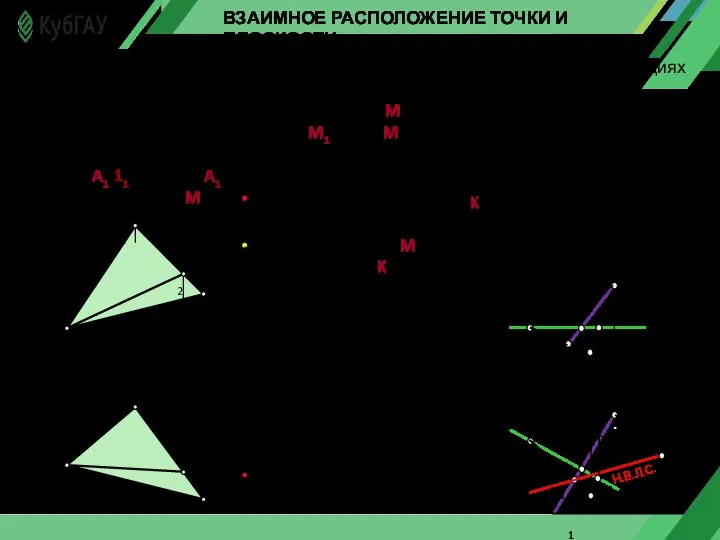
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ И ПЛОСКОСТИ
Точка лежит в плоскости, если ее проекции находятся на одноименных проекциях
какой-либо прямой, принадлежащей данной плоскости.
Произвольно выбирают одну проекцию точки M, например, фронтальную ее проекцию M2 .
Искомую горизонтальную проекцию M1 точки M находят по линиям связи на горизонтальной
проекции (A1 11) прямой A1 плоскости. Таких вспомогательных прямых в плоскости можно
провести через точку M бесчисленное множество. Одна из них и представлена на эпюре.
Если взять точку K горизонтально конкурирующую
с точкой M и расположенную над ней, то точка K
будет расположена и над плоскостью.
22
21
∆z
∆z
11
32
А0
Н.В.Л.С.

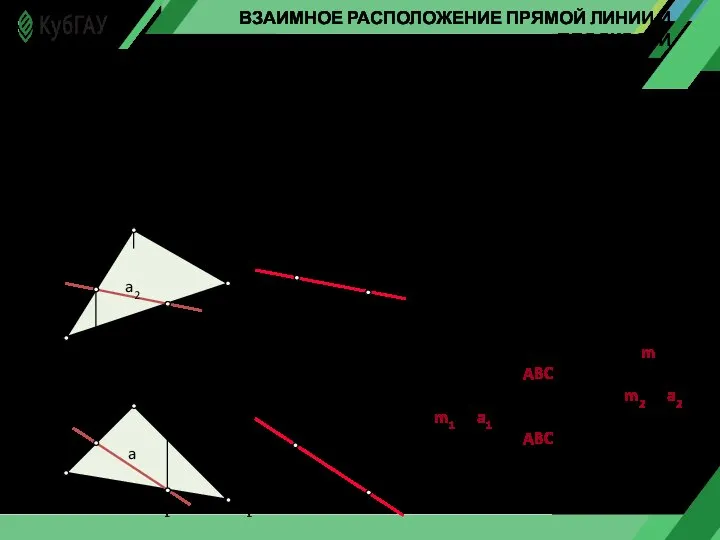
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ ЛИНИИ И ПЛОСКОСТИ
Возможны следующие три случая относительного расположения прямой и плоскости:
прямая принадлежит плоскости, прямая параллельна плоскости, прямая пересекает плоскость.
На основании свойства плоскости: если прямая линия соединяет две точки данной плоскости, то такая прямая всеми своими точками лежит в этой плоскости. Построение прямых, принадлежащих плоскости рассмотрены на слайде (главные линии плоскости).
K2
m2
K1
m1
Из стереометрии известно: если прямая параллельна плоскости, то она параллельна одной из
прямых, лежащих в этой плоскости. На эпюре параллельность прямой m и плоскости ABC
доказывается тем, что m2 // a2, m1 // a1 ; прямая принадлежит плоскости ABC.

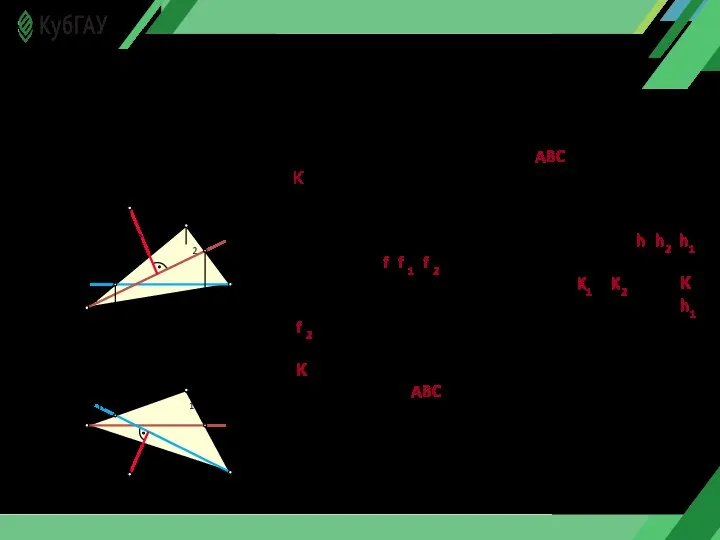
Если прямая линия пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются перпендикулярно проекциям соответствующих линий уровня плоскости.
Если, например, на плоскость, заданную треугольником ABC, необходимо опустить перпендикуляр из точки К, то построение выполняют следующим образом.
На плоскости проводят горизонталь h (h2, h1) и фронталь f (f 1, f 2).
Затем из заданных проекций K1 и K2 точки К опускают перпендикуляры соответственно на h1 и f 2.
Прямая, проведенная таким образом из точки К, будет перпендикулярна плоскости треугольника ABC (так как прямая, перпендикулярная плоскости должна быть перпендикулярна двум прямым, лежащим в этой плоскости).

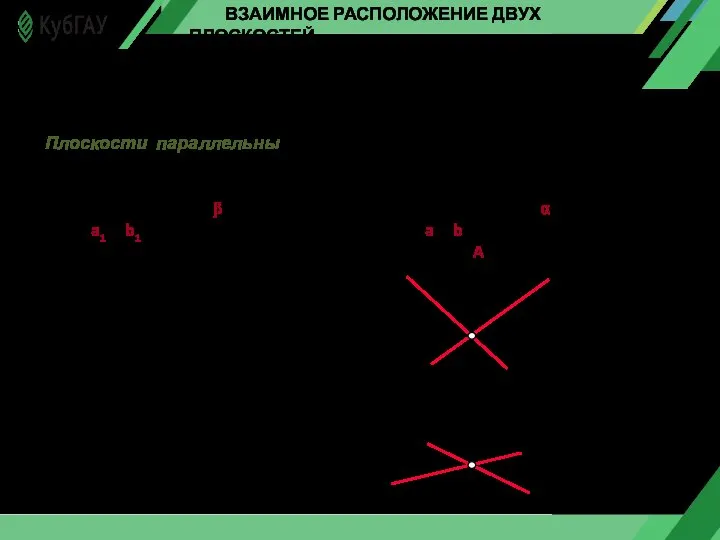
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ
Две плоскости в пространстве могут быть либо взаимно параллельными, либо пересекающимися.
Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Искомая плоскость β, параллельная заданной плоскости α, определена прямыми a1 и b1 соответственно параллельными a и b заданной плоскости и проходящими через произвольную точку пространства A.

Определение линии пересечения двух плоскостей общего положения
Для определения точек линии пересечения обе заданные плоскости a и b пересекают двумя вспомогательными (параллельными между собой) плоскостями-посредниками. Некоторое упрощение можно достичь, если вспомогательные плоскости проводить через прямые, задающие плоскость.
Рассмотрим пример. Плоскость a задана (ABC), плоскость b задана (DEK). Точки M и N, определяющие искомую линию пересечения двух данных плоскостей найдем как точки пересечения каких-либо двух сторон (как две прямые) треугольника ABC с плоскостью другого треугольника DEK, т.е. дважды решим позиционную задачу на определение точки пересечения прямой с плоскостью по рассмотренному алгоритму.
Выбор сторон треугольников произволен, так как только построением можно точно определить, какая действительно сторона и какого треугольника пересечет плоскость другого. Выбор плоскости-посредника также произволен, так как прямую общего положения, какими являются все стороны треугольников ABC и DEK, можно заключить в горизонтально проецирующую или во фронтально проецирующую плоскости.

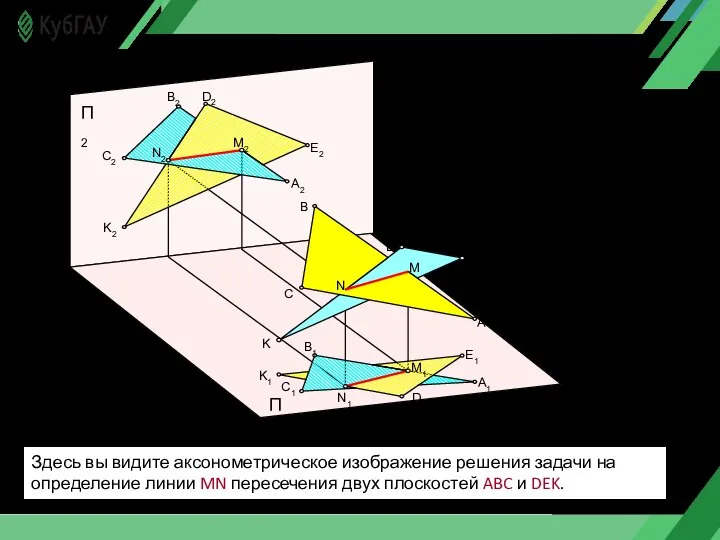
Здесь вы видите аксонометрическое изображение решения задачи на определение линии MN пересечения двух плоскостей ABC и DEK.
Y

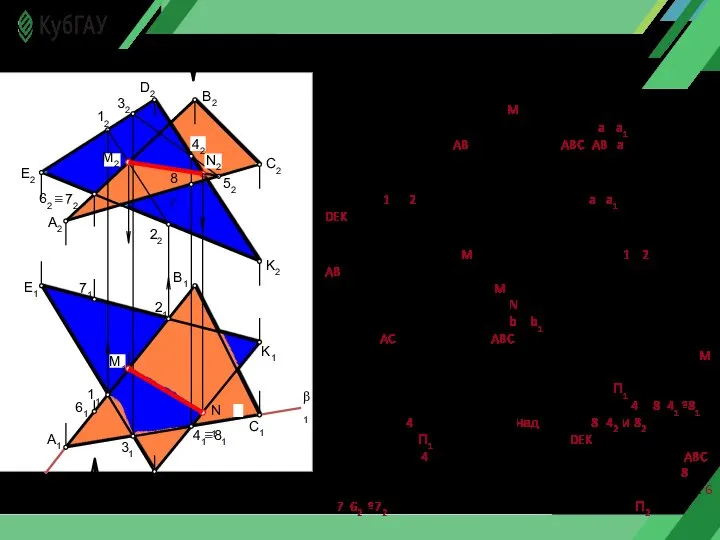
M2
12
42
31
41
11
N1
D1
α1
21
B1
1-й этап решения
Для построения точки M использована горизонтально проецирующая плоскость - посредник a (a1), в которую заключена сторона AB треугольника ABC (AB Ì a).
2-й этап решения.
Строим линию пересечения (на чертеже она задана точками 1 и 2) плоскости-посредника a (a1) и плоскости DEK.
3-й этап решения.
Находим точку M пересечения прямой 1 - 2 с прямой AB.
Найдена одна точка M искомой линии пересечения.
Для построения точки N использована горизонтально проецирующая плоскость b (b1), в которую заключена сторона AC треугольника ABC.
Построение аналогичны предыдущим. одна точка M искомой линии пересечения.
Определение видимости на плоскости П1 выполнено с помощью горизонтально конкурирующих точек 4 и 8 (41 º81).
Точка 4 расположена над точкой 8 (42 и 82), поэтому на плоскости П1 часть треугольника DEK, расположенная в сторону точки 4, закрывает собой часть треугольника ABC, расположенную от линии пересечения в сторону точки 8.
С помощью пары фронтально конкурирующих точек 6 и 7 (62 º72) определена видимость на плоскости П2.

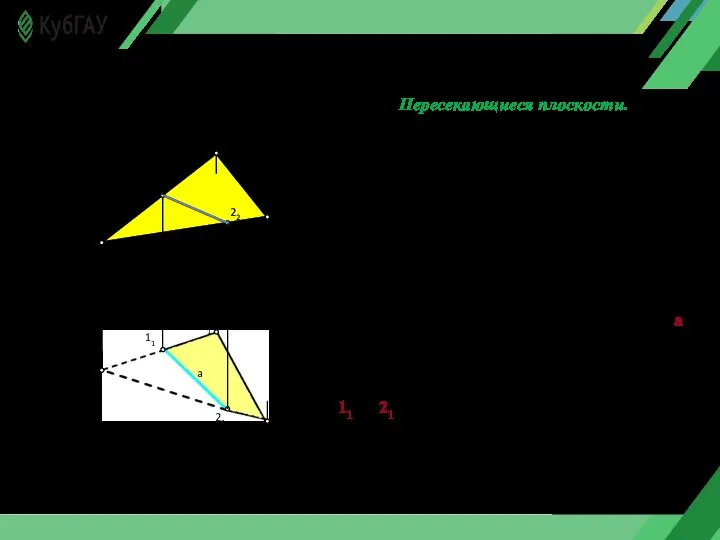
Пересекающиеся плоскости.
Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две точки, общие обеим плоскостям.
Если одна из пересекающихся плоскостей занимает частное положение, то ее вырожденная проекция (след плоскости) включает в себя и проекцию линии a пересечения плоскостей.
Горизонтальную проекцию прямой строят по двум общим с плоскостью точкам 11 и 21. На горизонтальной проекции часть ∆ 11,А1,21 будет не видима, т.к находится ниже проецирующего следа РП1.
12
21
11
22
a

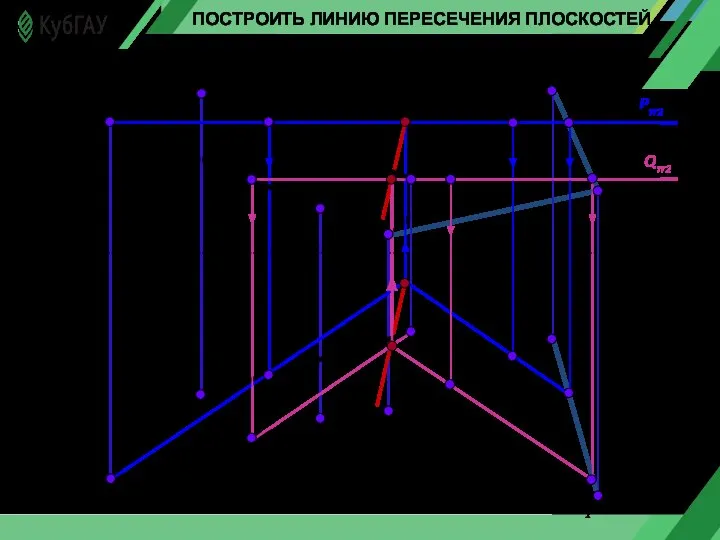
Х
А1
А2
С2
С1
В1
В2
0
Pπ2
ПОСТРОИТЬ ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ
11
12
22
21
D2
E2
N2
F2
D1
E1
N1
F1
Qπ2
31
41
51
61
K1
L1
32
42
52
62
K2
L2

АЛГОРИТМ ПОСТРОЕНИЯ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ:
1. Для решения задачи воспользуемся двумя вспомогательными секущими плоскостями уровня.
2. Определяем линию пересечения первой вспомогательной плоскости Рп1 с заданными плоскостями ( АВ и СD; и ∆ЕNF) там, где на горизонтальной проекции эти 2 линии между собой пересекаются, находим точку К1 – общую для трех плоскостей. Фронтальная проекция точки К лежит на фронтальном следе плоскости Рп2 .
3. Со второй секущей плоскостью Qп2 делаем аналогичные построения. Находим общую точку для трех плоскостей К1\ ; К2\ . Одноименные проекции точек соединяем.

Если плоскость задается частного положения и требуется определить точку встречи прямой с плоскостью, необходимо вспомнить о собирательном свойстве одного из следов плоскости. А согласно этому свойству точка встречи всегда лежит на собирательном следе. Значит остается найти вторую проекцию точки встречи.
1)
Pп1
0
А2
2)
х
А2
х
Pп1
Рх
В2
В1
к2
А1
к1
0
В2
В1
к2
А1
Рп1
к1
х
0
3)
D2
E2
к2
А2
С2
А1
С1
В1
D1
E1
к1
В2
Если задана плоскость общего положения и прямая, то для нахождения точки пересечения прямой с плоскостью необходимо сделать следующие построения:
1) заключить прямую в плоскость частного положения;
2) Построить линию пересечения заданной плоскости со вспомогательной;
3) Определить точку пересечения прямой с плоскостью;
4) Определить видимость прямой.
ПОСТРОЕНИЕ ТОЧКИ ВСТРЕЧИ ПРЯМОЙ С ПЛОСКОСТЬЮ
(2-Я ОСНОВНАЯ ЗАДАЧА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ)

Пример 2. Определить точку встречи прямой с плоскостью общего положения.
0
А2
А1
В2
В1
Рх
А2
А1
Рп2
12
11
=
х
П1
П4
А4
Рп1
Рх '
В4
=
Рп4
к4
14
Рп2
П2
П1
х
х
х
0
П2
П1
Рх
12
11
Рп1
П1
П4
Рх '
14
Рп4
Пример 1. Преобразовать методом замены плоскостей эпюр таким образом, чтобы плоскость общего положения стала проецирующей (частного положения).

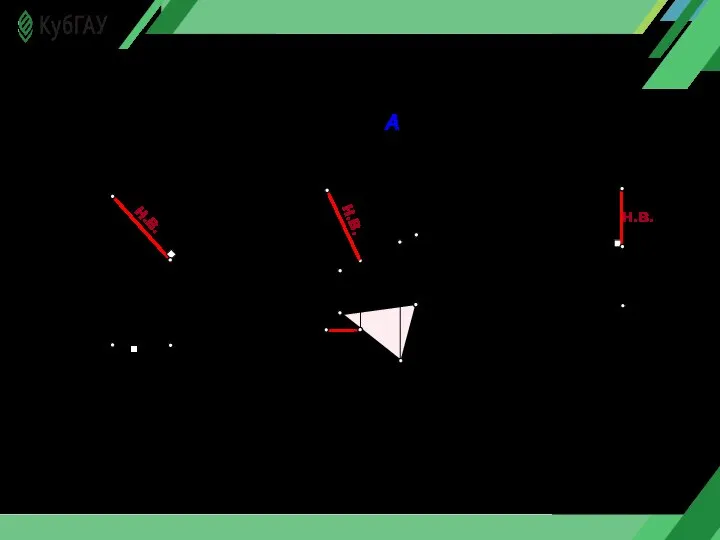
Если плоскость до которой определяем расстояние является плоскостью частного положения, задача решается очень просто.
Собирательное свойство плоскости частного положения дает нам возможность сразу определить на следе точку пересечения перпендикуляра, опущенного из точки к собирательному следу плоскости. Вторая проекция точки встречи находится по линии проекционной связи.
Опустить перпендикуляр к плоскости заданной следами, это значит провести его на проекциях перпендикулярно соответствующим следам плоскости(согласно теореме о проекции прямого угла).
Если плоскость частного положения задана треугольником или любым другим способом, перпендикуляр из точки нужно проводить на той проекции где треугольник или другой геометрический образ проецировался в одну линию. Определим точку «К», а на второй проекции перпендикуляр, проведенный из точки «К» будет всегда оси ох, т.к. на первой проекции он проецируется в натуральную величину.
Если задается плоскость общего положения до которой нужно определить расстояние, нужно преобразовывать эпюр таким образом, чтобы эта плоскость стала проецирующей, а затем решать, как примеры 1, 2, 3
ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ТОЧКИ ДО ПЛОСКОСТИ.
( 3-Я ОСНОВНАЯ ЗАДАЧА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ).

1)
х
н.в.
А2
К2
К1
А1
Рх
Рп2
Рп1
3)
х
Рп2
н.в.
А2
К2
К1
А1
2)
х
А1
С1
В1
В2
D2
А2
К2
D1
н.в.
С2
К1
Определение расстояние от точки А до частного положения плоскости

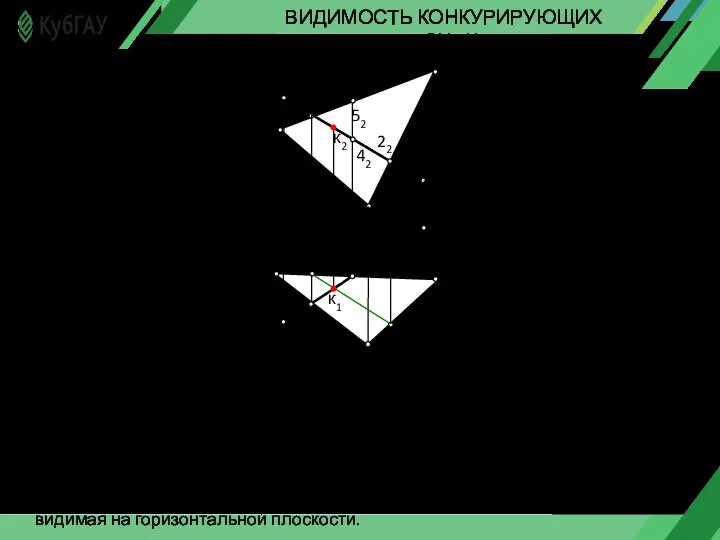
С2
В2
D2
E2
S2
А2
А1
В1
С1
S1
D1
E1
х
Рп2
12
22
11
21
к1
к2
32
31
41
51
42
52
Для того, чтобы определить видимость на горизонтальной проекции нужно:
конкурирующие точки 41;51 обозначить на горизонтальной проекции, найти их проекции на фронтальной плоскости;
определить, у которой из точек большая координата Z, та прямая и будет видимая на горизонтальной плоскости.
ВИДИМОСТЬ КОНКУРИРУЮЩИХ ТОЧЕК

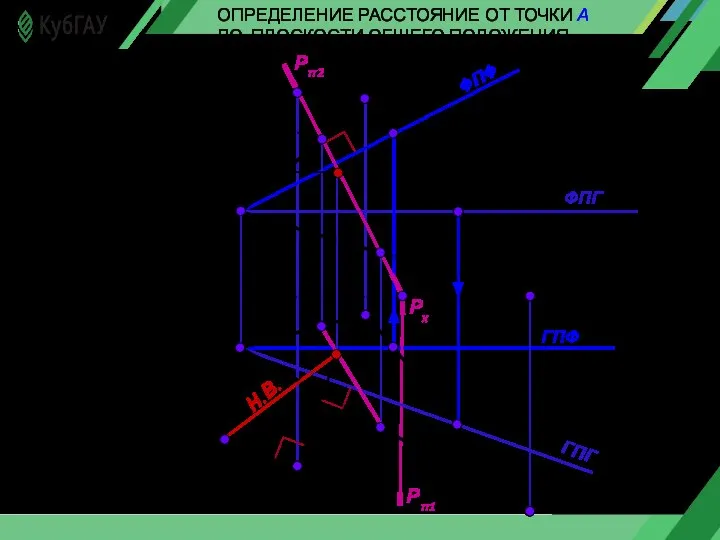
ОПРЕДЕЛЕНИЕ РАССТОЯНИЕ ОТ ТОЧКИ А ДО ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
Х
А1
А2
К1
K2
Н.В.
0
Рπ1
С1
В1
D1
C2
B2
D2
11
ФПФ
ГПФ
12
22
21
ФПГ
ГПГ
Рπ2
Рx
31
42
41
ΔZ
ΔZ
А0
32