Наращение и дисконтирование

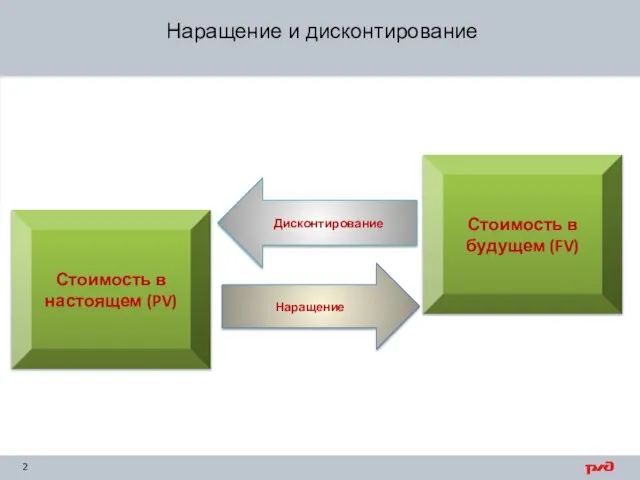
Стоимость в настоящем (PV)
Стоимость в будущем (FV)
Наращение и дисконтирование
Дисконтирование
Наращение

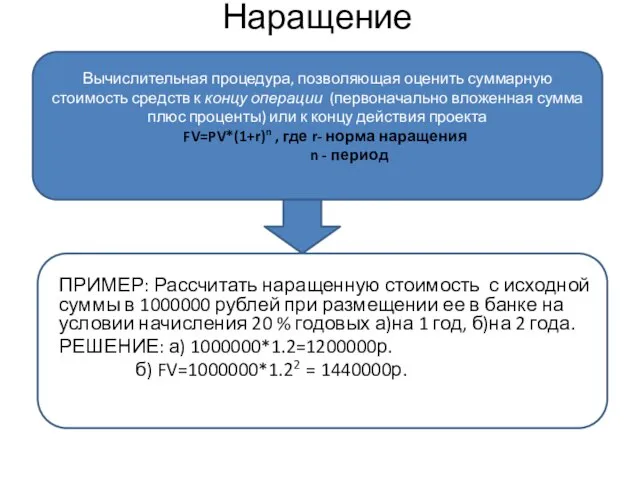
Наращение
ПРИМЕР: Рассчитать наращенную стоимость с исходной суммы в 1000000 рублей при размещении ее в банке на условии начисления 20 % годовых а)на 1 год, б)на 2 года.
РЕШЕНИЕ: а) 1000000*1.2=1200000р.
б) FV=1000000*1.22 = 1440000р.
Вычислительная процедура, позволяющая оценить суммарную стоимость средств к концу операции (первоначально вложенная сумма плюс проценты) или к концу действия проекта
FV=PV*(1+r)n , где r- норма наращения
n - период

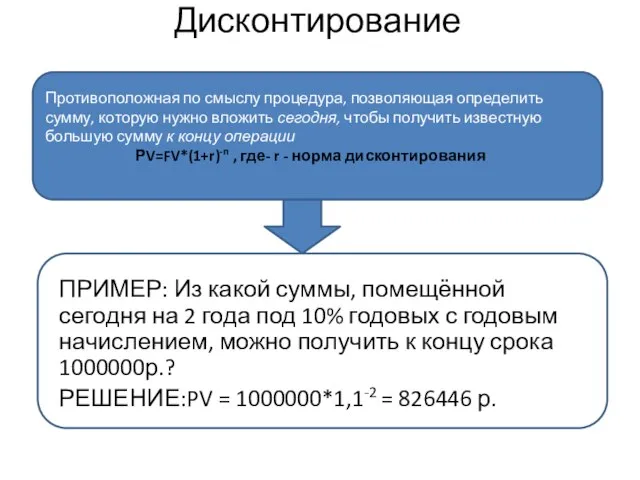
Дисконтирование
ПРИМЕР: Из какой суммы, помещённой сегодня на 2 года под 10% годовых с годовым начислением, можно получить к концу срока 1000000р.?
РЕШЕНИЕ:PV = 1000000*1,1-2 = 826446 р.
Противоположная по смыслу процедура, позволяющая определить сумму, которую нужно вложить сегодня, чтобы получить известную большую сумму к концу операции
РV=FV*(1+r)-n , где- r - норма дисконтирования

Дисконтированная стоимость денежных потоков
ПРИМЕР: Предполагается, что чистый доход предприятия от вложения 1000000 р. составляет в 1 год 500000 р, во второй год 800000 р. Дисконтированная стоимость денежного потока при 20% ставке дисконта:
РV = 500000*0.8333+800000*0.6944=972170 р.
Оценка денежных потоков, ожидаемых к получению в будущем, с позиции настоящего времени
РV=FV*(1+r)-n при единичном денежном потоке
П
ри денежных потоках с периодическими поступлениями

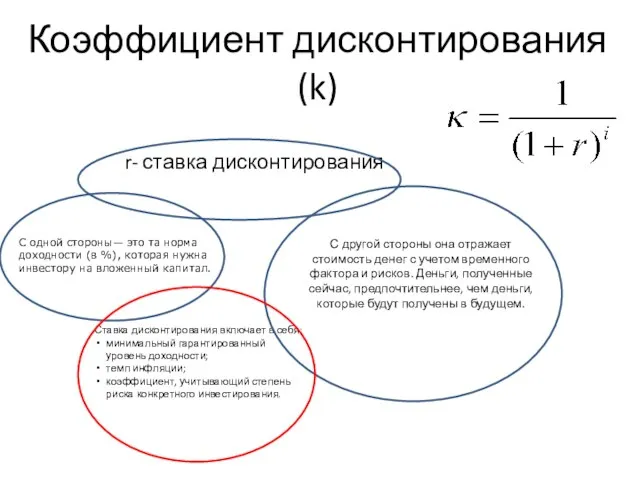
Коэффициент дисконтирования (k)
r- ставка дисконтирования
С одной стороны— это та норма доходности (в %), которая нужна инвестору на вложенный капитал.
С другой стороны она отражает стоимость денег с учетом временного фактора и рисков. Деньги, полученные сейчас, предпочтительнее, чем деньги, которые будут получены в будущем.
Ставка дисконтирования включает в себя:
минимальный гарантированный уровень доходности;
темп инфляции;
коэффициент, учитывающий степень риска конкретного инвестирования.

Шесть функций сложного процента (шесть функций денежной единицы)
Эти функции позволяют определять будущую или текущую оценку как одиночного платежа, так и потока платежей (Cash flow), а также величины платежей, которые необходимо производить для формирования денежных потоков с заданными значениями их будущих или текущих оценок.

1. Будущая стоимость денежной единицы(future value of one)

2. Накопление единицы за период(Accumulation of one per period)

3. Фактор фонда возмещения (Sinking fund)

4. Текущая стоимость денежной единицы (present worth (value) of one)

5. Текущая стоимость аннуитета (Present worth (value) of annuity)

5-а. Текущая стоимость бессрочного аннуитета (Present Value of the Perpetuity)

6. Взнос на амортизацию единицы (Installment to amortize one)