Ортотреугольник и его свойства

Италия, начало XVIII века
Инженер и математик Фаньяно Дей Тоски (1682—1766)
Задача: вписать в данный остроугольный треугольник ABC треугольник наименьшего периметра так, чтобы на каждой стороне треугольника ABC лежала одна вершина треугольника.
Существует единственный вписанный треугольник наименьшего периметра - ортотреугольник.

Цель данной работы:
описание дополнительных геометрических свойств треугольника.
Задачи:
1) выяснить, что такое ортотреугольник;
2) изучить его свойства;
3) рассмотреть возможное применение
этих свойств к решению задач.

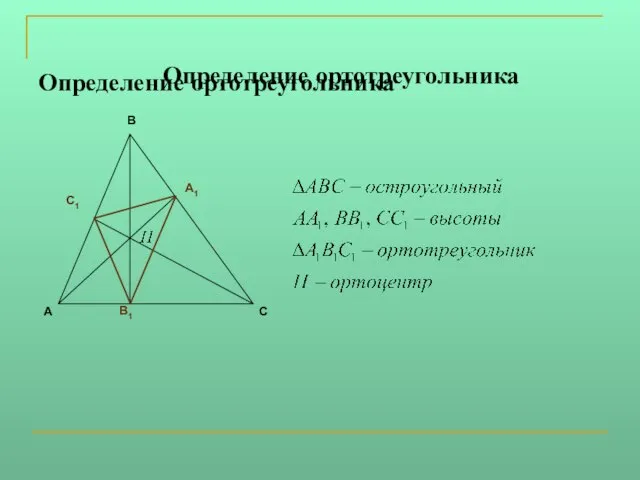
Определение ортотреугольника
Определение ортотреугольника

Свойства ортотреугольника
Ортотреугольник отсекает треугольники, подобные данному.
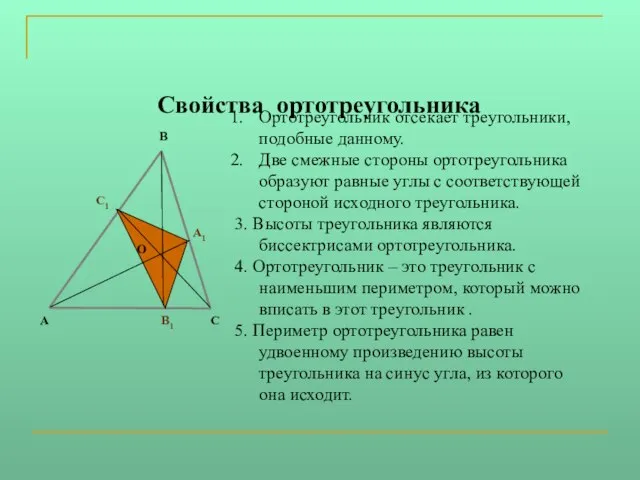
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
3. Высоты треугольника являются биссектрисами ортотреугольника.
4. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .
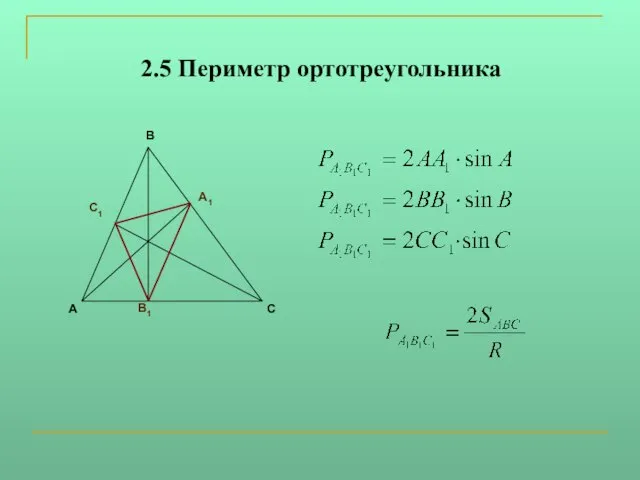
5. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.

2.1 Теорема о подобии треугольников
1.
Ортотреугольник отсекает треугольники, подобные данному.

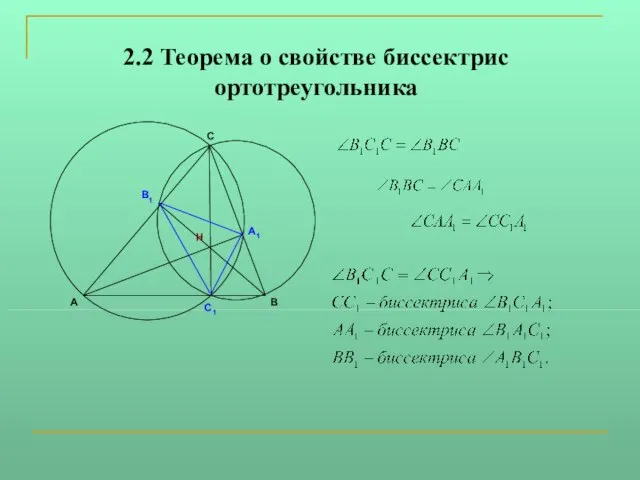
2.2 Теорема о свойстве биссектрис ортотреугольника
В

2.3 Теорема Фаньяно
Среди всех треугольников, вписанных в данный
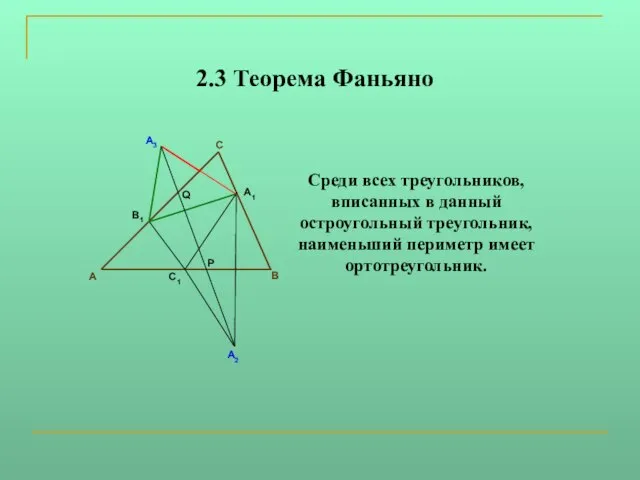
остроугольный треугольник, наименьший периметр имеет ортотреугольник.

2.4 Физический смысл
и механическая модель задачи Фаньяно

2.5 Периметр ортотреугольника

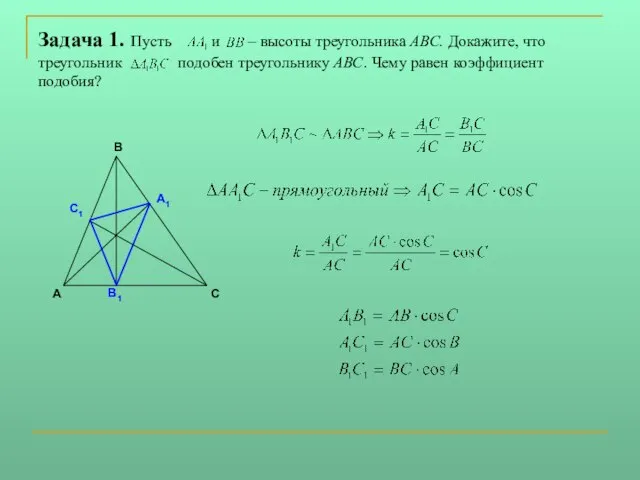
Задача 1. Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?

Задача 3. В остроугольном треугольнике АВС проведены высоты АD, ВЕ и СF.Докажите, что pR=Pr, где p-периметр треугольника EDF, Р – периметр треугольника АВС.