Пересечение поверхности вращения плоскостью. Развертка нижней отсеченной части конуса. Лекция 11

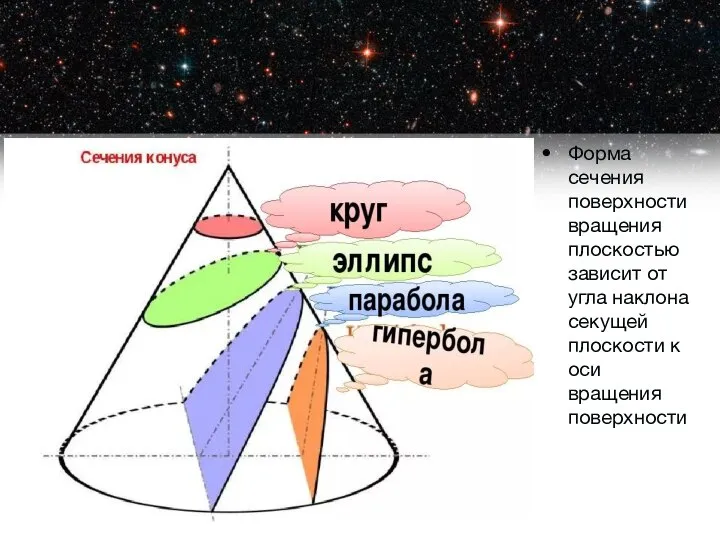
Форма сечения поверхности вращения плоскостью зависит от угла наклона секущей плоскости к оси вращения поверхности

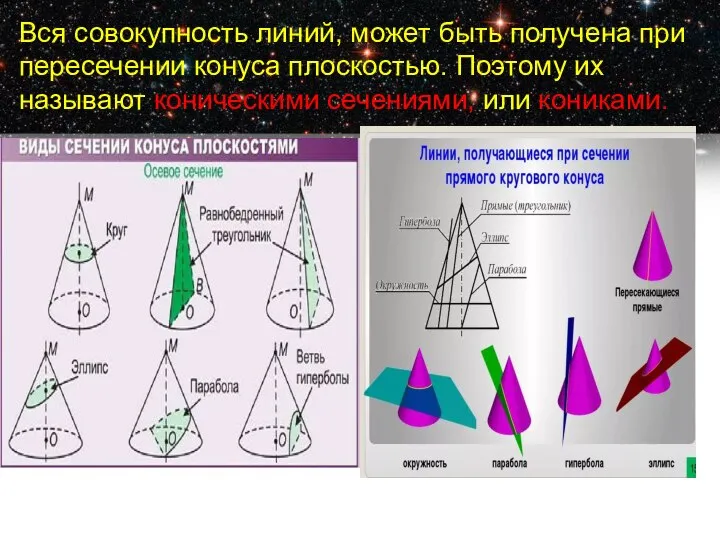
Вся совокупность линий, может быть получена при пересечении конуса плоскостью. Поэтому их называют коническими сечениями, или кониками.

Сечения прямого кругового конуса
При пересечении прямого кругового конуса с плоскостью в зависимости от ее расположения получаются:
1 – окружность; 2 – эллипс; 3 – парабола; 4 – гипербола;
5 – прямые линии

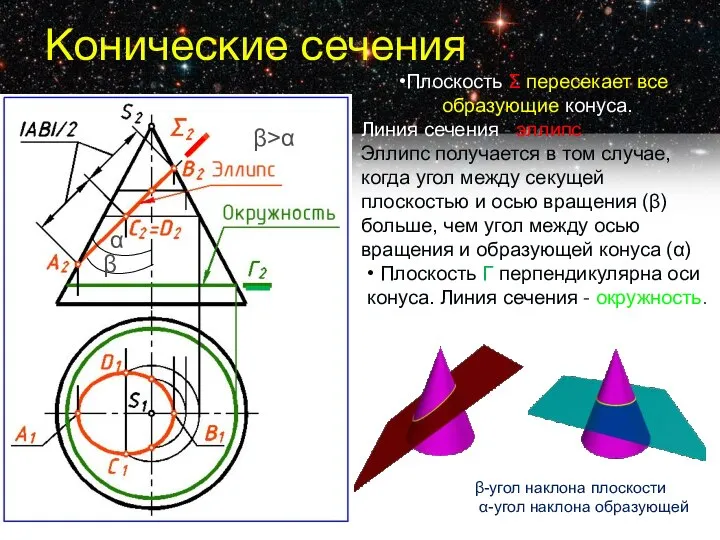
Конические сечения
Плоскость Σ пересекает все образующие конуса.
Линия сечения - эллипс.
Эллипс получается в том случае, когда угол между секущей плоскостью и осью вращения (β) больше, чем угол между осью вращения и образующей конуса (α)
Плоскость Г перпендикулярна оси конуса. Линия сечения - окружность.
α
β
β>α
β-угол наклона плоскости
α-угол наклона образующей

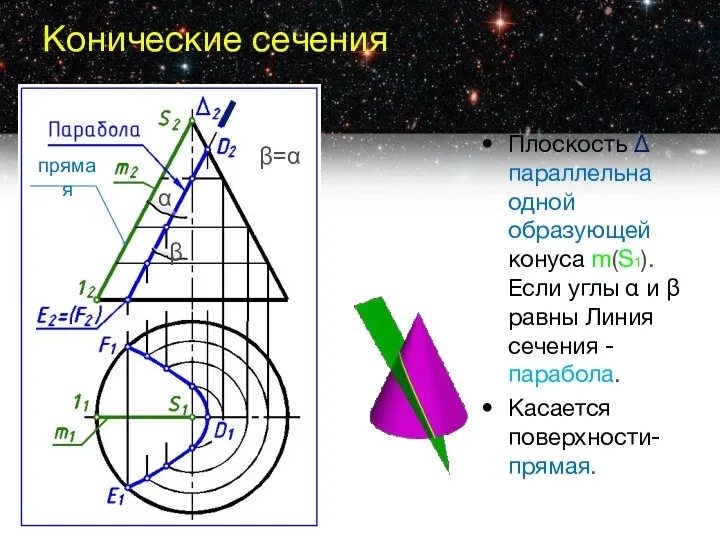
Конические сечения
Плоскость Δ параллельна одной образующей конуса m(S1). Если углы α и β равны Линия сечения - парабола.
Касается поверхности- прямая.
α
β
β=α
прямая

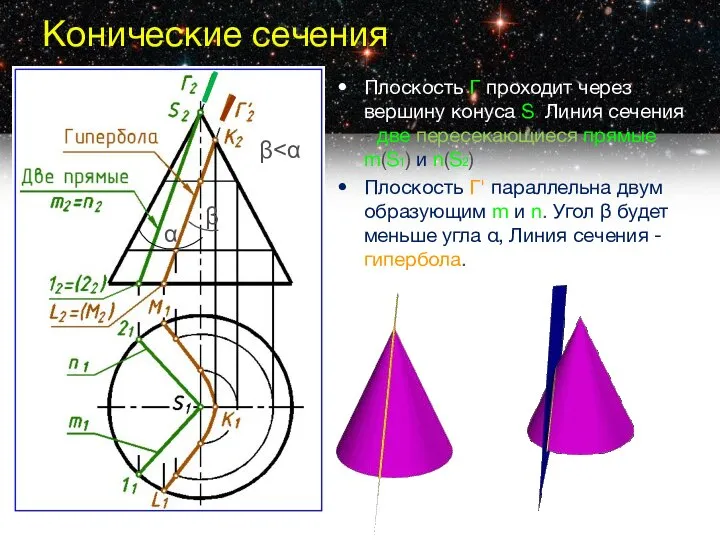
Конические сечения
Плоскость Г проходит через вершину конуса S. Линия сечения - две пересекающиеся прямые m(S1) и n(S2)
Плоскость Г' параллельна двум образующим m и n. Угол β будет меньше угла α, Линия сечения - гипербола.
β<α
β
α

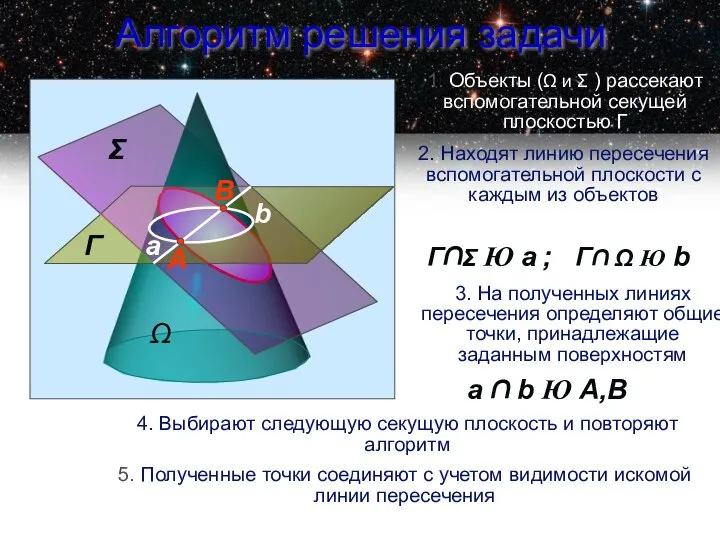
Алгоритм решения задачи
1. Объекты (Ω и Σ ) рассекают вспомогательной секущей плоскостью Г
2. Находят линию пересечения вспомогательной плоскости с каждым из объектов
4. Выбирают следующую секущую плоскость и повторяют алгоритм
5. Полученные точки соединяют с учетом видимости искомой линии пересечения
a ∩ b Ю A,B
3. На полученных линиях пересечения определяют общие точки, принадлежащие заданным поверхностям
Ω
Σ

Для построения линии пересечения необходимо найти общие точки поверхности и заданной плоскости. Для определения этих точек необходимо ввести дополнительные секущие плоскости, которые дают наиболее простые линии сечения – окружности или ломаные прямые.
Построение линии сечения начинают с нахождения характерных точек сечения, к которым относятся:
высшая и низшая точки;
крайняя левая и крайняя правая точки, в которых проекции линии сечения касаются очерковых образующих ( точки, лежащие на границе видимости);
ближайшая и наиболее удаленная точки сечения.
ПРИМЕР: Определить линию пересечения конуса плоскостью общего положения Θ (h∩f).
Построить развертку нижней отсеченной поверхности конуса.

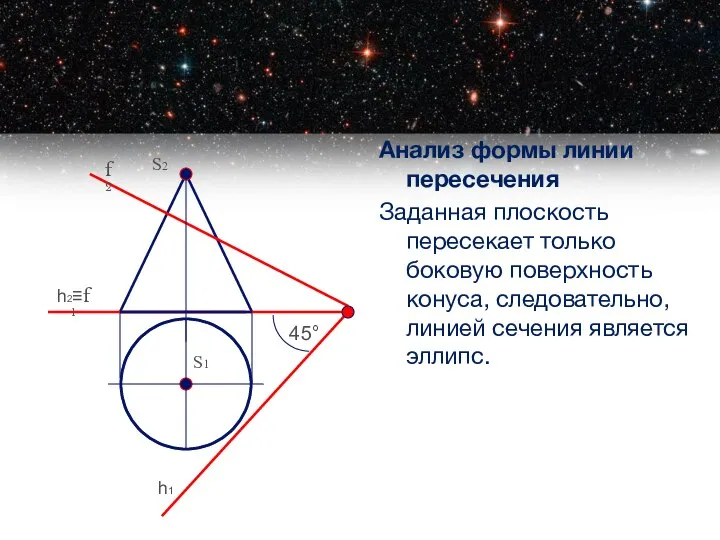
Анализ формы линии пересечения
Заданная плоскость пересекает только боковую поверхность конуса, следовательно, линией сечения является эллипс.
S2
S1
f2
h1
h2≡f1
45°

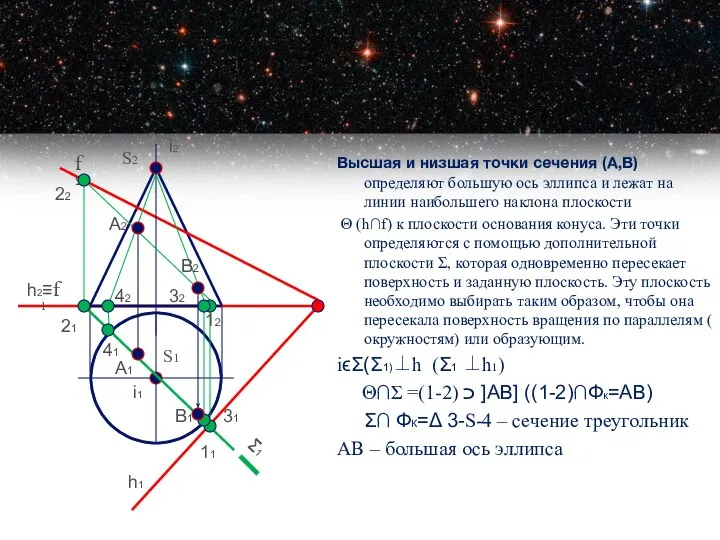
Высшая и низшая точки сечения (А,В) определяют большую ось эллипса и лежат на линии наибольшего наклона плоскости
Θ (h∩f) к плоскости основания конуса. Эти точки определяются с помощью дополнительной плоскости Σ, которая одновременно пересекает поверхность и заданную плоскость. Эту плоскость необходимо выбирать таким образом, чтобы она пересекала поверхность вращения по параллелям ( окружностям) или образующим.
iϵΣ(Σ1)⊥h (Σ1 ⊥h1)
Θ∩Σ =(1-2) ﬤ ]AB] ((1-2)∩Фк=АВ)
Σ∩ Фк=Δ 3-S-4 – сечение треугольник
АВ – большая ось эллипса
S2
S1
f2
h1
h2≡f1
11
12
Σ1
В1
В2
А1
А2
42
41
32
31
21
22
i2
i1

[AВ]делим отрезок пополам
0- центр эллипса
[A0]=[0B]
S2
S1
f2
h1
h2≡f1
11
12
Σ1
В1
В2
А1
А2
42
41
32
31
21
22
i2
i1
02
01

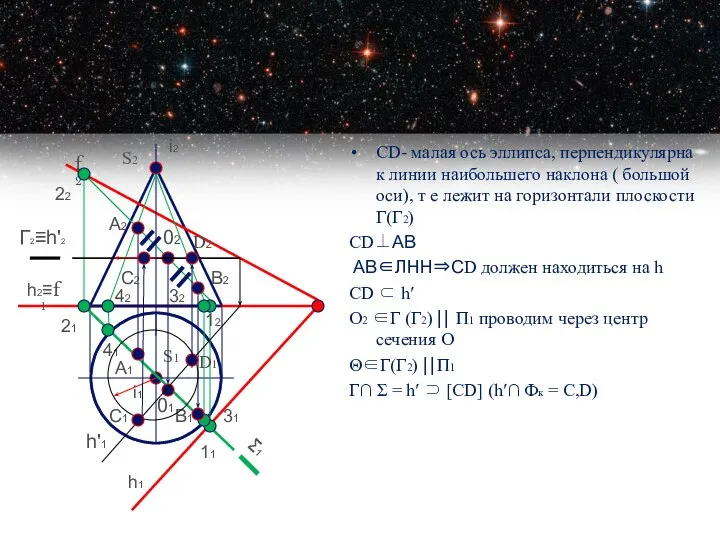
СD- малая ось эллипса, перпендикулярна к линии наибольшего наклона ( большой оси), т е лежит на горизонтали плоскости Г(Г2)
СD⊥AB
AB∈ЛНН⇒СD должен находиться на h
СD ⊂ hʹ
О2 ∈Г (Г2) ⎢⎢ П1 проводим через центр сечения О
Θ∈Г(Г2) ⎢⎢П1
Г∩ Σ = hʹ ⊃ [СD] (hʹ∩ Фк = С,D)
S2
S1
f2
h1
h2≡f1
11
12
Σ1
В1
В2
А1
А2
42
41
32
31
21
22
i2
i1
02
01
Г2≡hʹ2
hʹ1
D2
D1
С2
С1

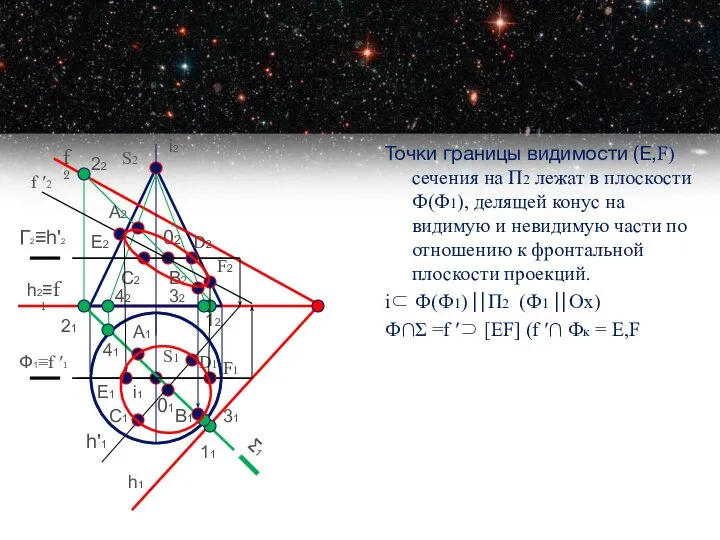
Точки границы видимости (Е,F) сечения на П2 лежат в плоскости Ф(Ф1), делящей конус на видимую и невидимую части по отношению к фронтальной плоскости проекций.
i⊂ Ф(Ф1) ⎢⎢П2 (Ф1 ⎢⎢Ох)
Ф∩Σ =f ʹ⊃ [ЕF] (f ʹ∩ Фк = Е,F
S2
S1
f2
h1
h2≡f1
11
12
Σ1
В1
В2
А1
А2
42
41
32
31
21
22
i2
i1
02
01
Г2≡hʹ2
hʹ1
D2
D1
С2
С1
F1
F2
Е1
Е2
Ф1≡f ʹ1
f ʹ2

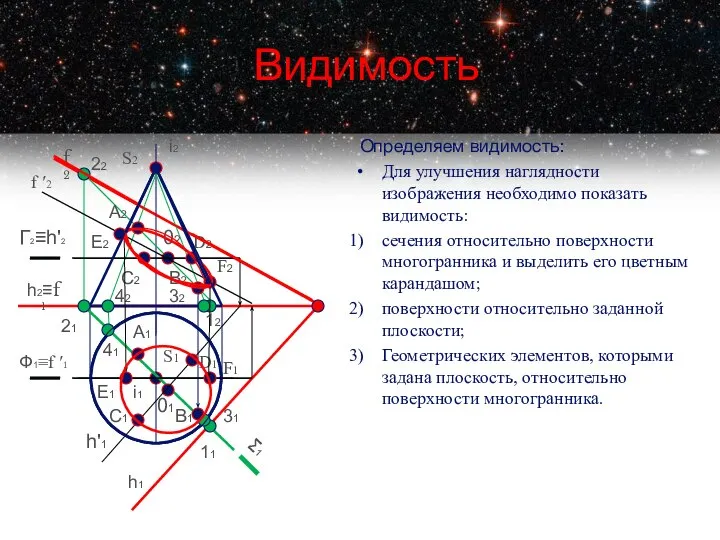
Видимость
Определяем видимость:
Для улучшения наглядности изображения необходимо показать видимость:
сечения относительно поверхности многогранника и выделить его цветным карандашом;
поверхности относительно заданной плоскости;
Геометрических элементов, которыми задана плоскость, относительно поверхности многогранника.
S2
S1
f2
h1
h2≡f1
11
12
Σ1
В1
В2
А1
А2
42
41
32
31
21
22
i2
i1
02
01
Г2≡hʹ2
hʹ1
D2
D1
С2
С1
F1
F2
Е1
Е2
Ф1≡f ʹ1
f ʹ2

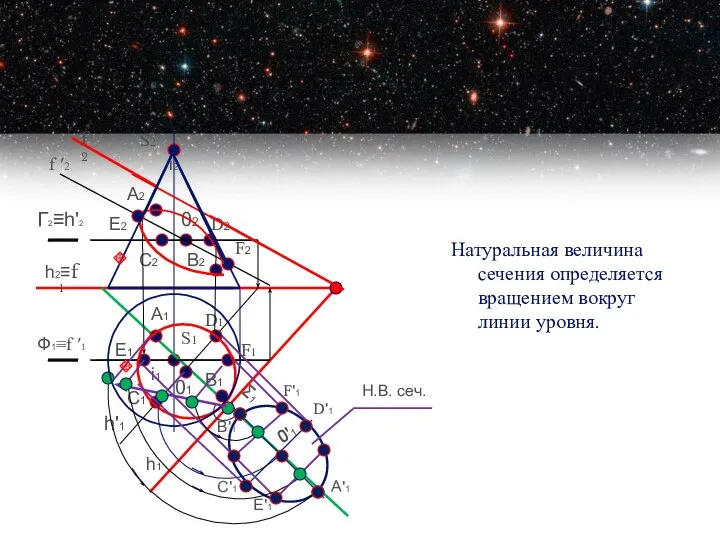
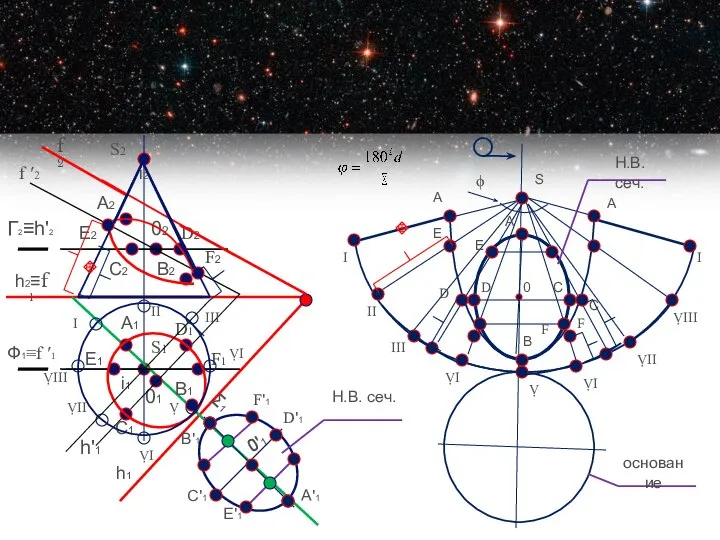
Натуральная величина сечения определяется вращением вокруг линии уровня.
S2
S1
f2
h1
h2≡f1
Σ1
В1
В2
А1
А2
i2
i1
02
01
Г2≡hʹ2
hʹ1
D2
D1
С2
С1
F1
F2
Е1
Е2
Ф1≡f ʹ1
f ʹ2
0ʹ1
Вʹ1
Fʹ1
Еʹ1
Сʹ1
Dʹ1
Аʹ1
Н.В. сеч.

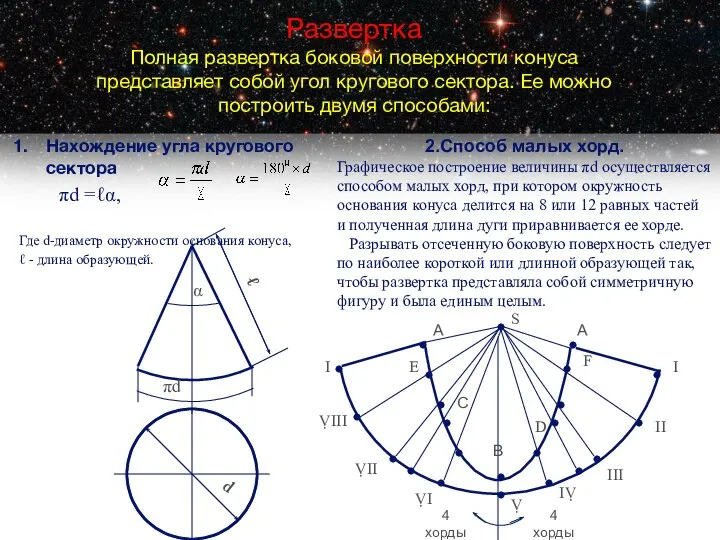
Нахождение угла кругового сектора
πd =ℓα,
Где d-диаметр окружности основания конуса,
ℓ - длина образующей.
Развертка
Полная развертка боковой поверхности конуса представляет собой угол кругового сектора. Ее можно построить двумя способами:
2.Способ малых хорд.
Графическое построение величины πd осуществляется способом малых хорд, при котором окружность основания конуса делится на 8 или 12 равных частей и полученная длина дуги приравнивается ее хорде.
Разрывать отсеченную боковую поверхность следует по наиболее короткой или длинной образующей так, чтобы развертка представляла собой симметричную фигуру и была единым целым.
ℓ
α
πd
d
ΙΙ
Ι
Ι
ΙΙΙ
ṾΙΙΙ
Ṿ
ΙṾ
ṾΙΙ
ṾΙ
F
D
В
С
E
А
А
S
4 хорды
4 хорды

S2
S1
f2
h1
h2≡f1
Σ1
В1
В2
А1
А2
i2
i1
02
01
Г2≡hʹ2
hʹ1
D2
D1
С2
С1
F1
F2
Е1
Е2
Ф1≡f ʹ1
f ʹ2
0ʹ1
Вʹ1
Fʹ1
Еʹ1
Сʹ1
Dʹ1
Аʹ1
Н.В. сеч.
Н.В. сеч.
основание
ϕ
D
А
А
А
Ṿ
С
0
F
Е
С
D
Е
F
Ι
ṾΙΙΙ
ΙΙΙ
ṾΙ
Ι
Ι
ΙΙ
ΙΙ
ΙΙΙ
ṾΙ
Ṿ
B
ṾΙΙ
ṾΙΙ
ṾΙ
ṾΙ
ṾΙΙΙ
S

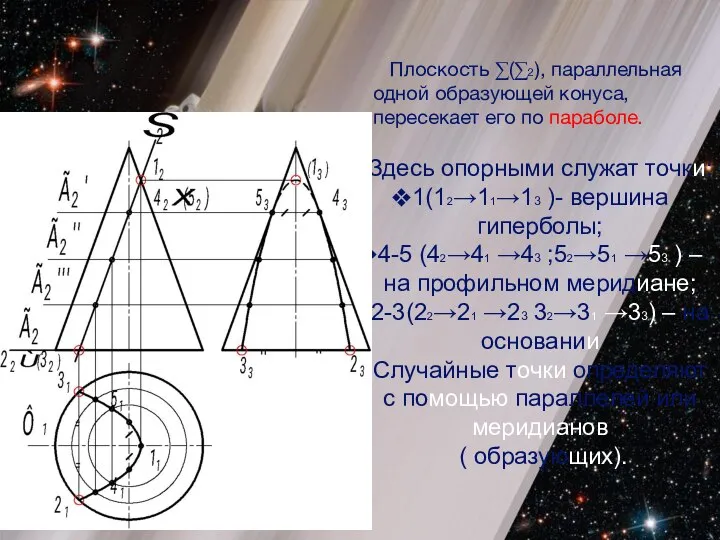
Плоскость ∑(∑2), параллельная одной образующей конуса, пересекает его по параболе.
Здесь опорными служат точки:
1(12→11→13 )- вершина гиперболы;
4-5 (42→41 →43 ;52→51 →53 ) – на профильном меридиане;
2-3(22→21 →23 32→31 →33) – на основании
Случайные точки определяют с помощью параллелей или меридианов
( образующих).

Гипербола получится в сечении, если плоскость∑(∑2) при пересечении с конусом параллельна одновременно двум образующим конуса (а-b)
Рассмотрим линию сечения, лежащую на поверхности конуса и его основания. Опорными служат точки:
С(С2→С1)- вершина параболы;
2(22→21) – на профильном меридиане;
М (М2→М1) N(N2→N1)– на основании
Случайные точки определяют с помощью параллелей или меридианов ( образующих).
22
21
2ʹ1
Г2
Гʹ2
Гʹʹ2
Гʹʹʹ2