Содержание
- 2. Содержание Определение пирамиды Правильная пирамида Усеченная пирамида Решение задач Итог урока Список литературы
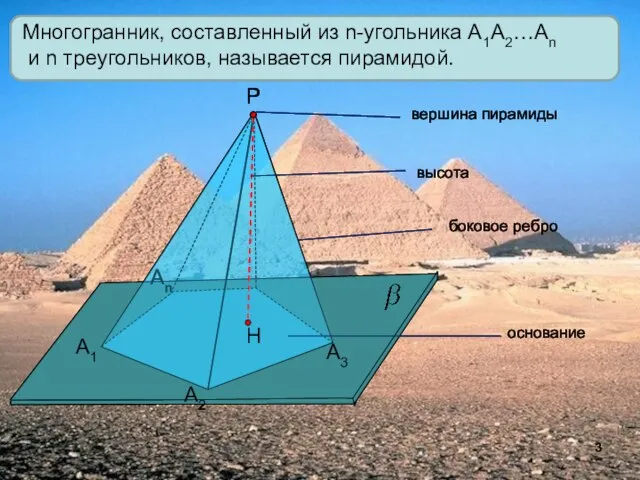
- 3. А1 А2 Аn Р А3 Многогранник, составленный из n-угольника А1А2…Аn и n треугольников, называется пирамидой. вершина
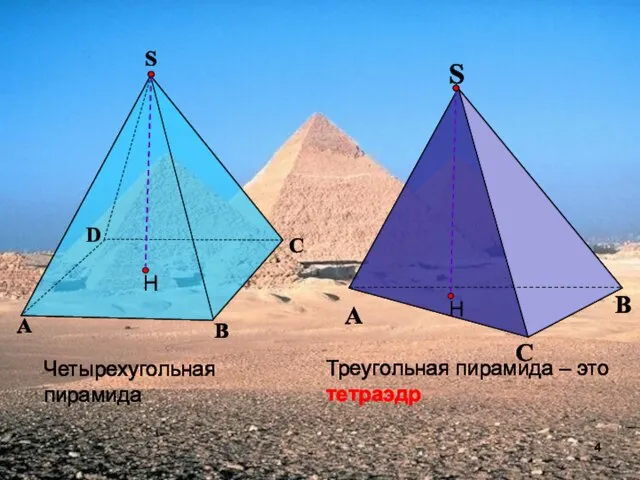
- 4. Треугольная пирамида – это тетраэдр Четырехугольная пирамида А B C D S
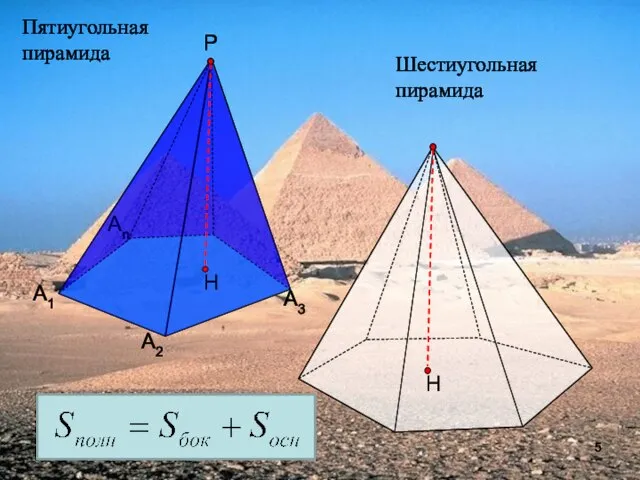
- 5. Пятиугольная пирамида А1 А2 Аn Р А3 Шестиугольная пирамида
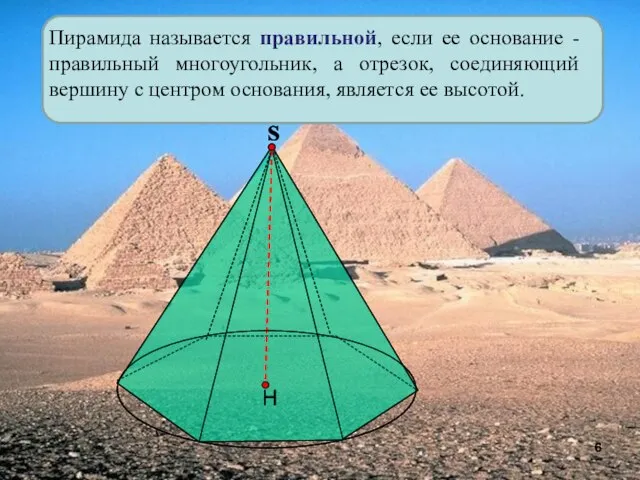
- 6. Пирамида называется правильной, если ее основание - правильный многоугольник, а отрезок, соединяющий вершину с центром основания,
- 7. Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками. А1 А2 А3
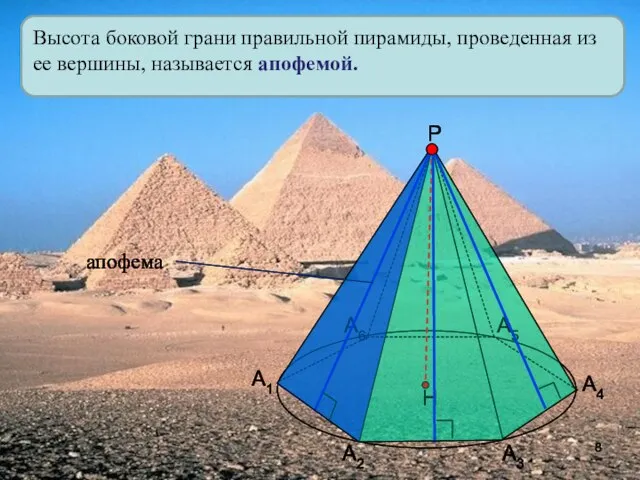
- 8. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. А1 А2 А3 А4 А5
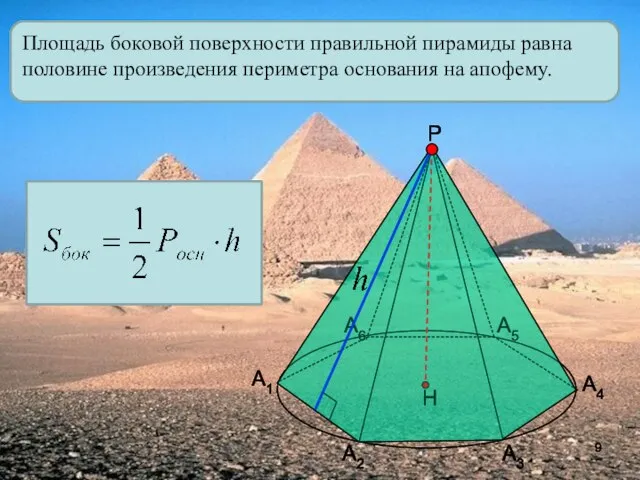
- 9. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. А1 А2 А3 А4
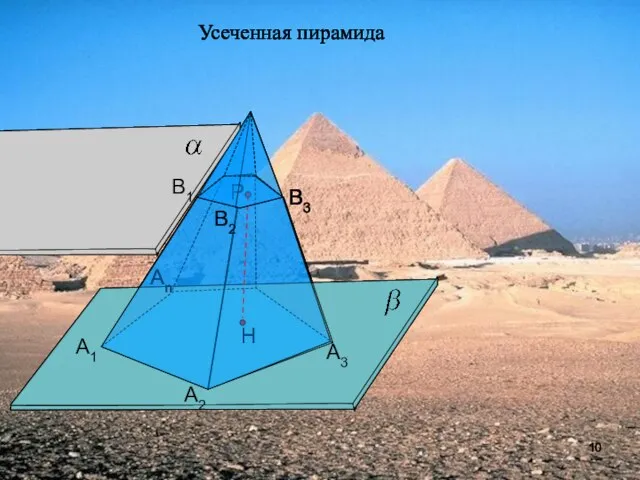
- 10. А1 А2 Аn А3 Усеченная пирамида
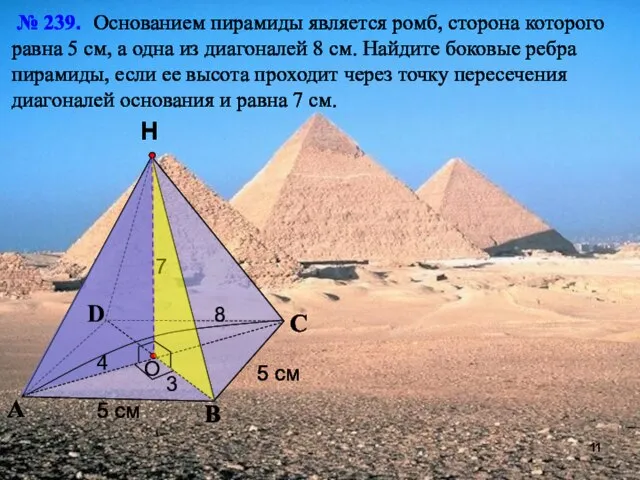
- 11. С А В Н № 239. Основанием пирамиды является ромб, сторона которого равна 5 см, а
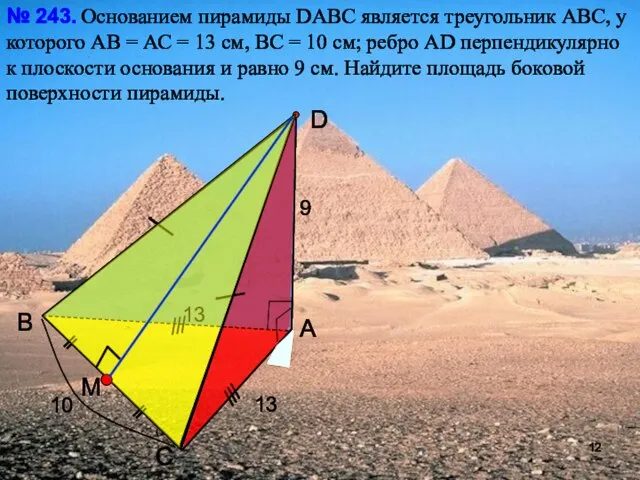
- 12. С В А D Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС =
- 13. Что называется пирамидой? Правильной пирамидой? Что называется площадью боковой поверхности пирамиды? Что называется площадью полной поверхности
- 14. Подведение итогов. Домашнее задание. П.32,33,34 №241,242
- 16. Скачать презентацию




 (–1) · 3 =
(–1) · 3 = Осмотр общего имущества в многоквартирном доме
Осмотр общего имущества в многоквартирном доме EV3 Самосвал
EV3 Самосвал Инвестиционный фонд МАП «Инновационный лифт»
Инвестиционный фонд МАП «Инновационный лифт» Нам нужны союзники!
Нам нужны союзники! Дисциплина: Международные перевозки грузов РАЗДЕЛ 3. Обеспечивающий комплекс организации международной перевозки грузов Тема 3
Дисциплина: Международные перевозки грузов РАЗДЕЛ 3. Обеспечивающий комплекс организации международной перевозки грузов Тема 3 Мое зазеркалье
Мое зазеркалье Московский колледж бизнес-технологий. Эксплуатация беспилотных авиационных систем
Московский колледж бизнес-технологий. Эксплуатация беспилотных авиационных систем Презентация Microsoft PowerPoint (3)
Презентация Microsoft PowerPoint (3) Презентация на тему Иудаизм презентация 4 класс
Презентация на тему Иудаизм презентация 4 класс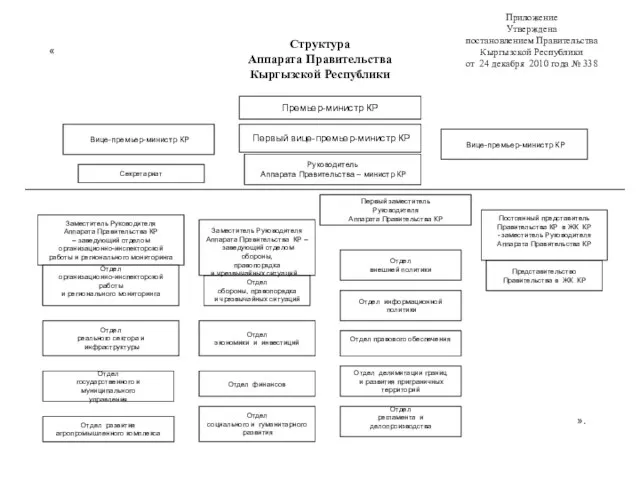 Структура Аппарата Правительства Кыргызской Республики
Структура Аппарата Правительства Кыргызской Республики Автоматизированная информационная система «Государственный заказ»
Автоматизированная информационная система «Государственный заказ» Формирование экологической культуры обучающихся колледжа через реализацию социально-образовательых проектов
Формирование экологической культуры обучающихся колледжа через реализацию социально-образовательых проектов Тема урока «Право на труд. Трудовые правоотношения»
Тема урока «Право на труд. Трудовые правоотношения» Класс 1-1 3주 후 시험문제 읽기 Чтение
Класс 1-1 3주 후 시험문제 읽기 Чтение Обобщающий урок - игра по теме: «Я знаю край родной».
Обобщающий урок - игра по теме: «Я знаю край родной». Тяжелая атлетика в России и за рубежом
Тяжелая атлетика в России и за рубежом Разработка мероприятия Цифровой текстиль. Синтетические ткани
Разработка мероприятия Цифровой текстиль. Синтетические ткани Лекция_6 ЭТД ФТД.ppt
Лекция_6 ЭТД ФТД.ppt Презентация на тему Сочинение по картине Левитана «Весна. Большая вода» 4 класс
Презентация на тему Сочинение по картине Левитана «Весна. Большая вода» 4 класс Методы мониторинга репутациив социальных медиа
Методы мониторинга репутациив социальных медиа Областной конкурспервичных профсоюзныхорганизаций.
Областной конкурспервичных профсоюзныхорганизаций. Контроль квалификации сварщиков. Система аттестации сварочного производства
Контроль квалификации сварщиков. Система аттестации сварочного производства Уголовное законодательство Республики Казахстан на страже воинского правопорядка (занятие 1)
Уголовное законодательство Республики Казахстан на страже воинского правопорядка (занятие 1) 36736
36736 Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс)
Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс) Электрическая лампа накаливания
Электрическая лампа накаливания 20161206_avstraliya-i-okeaniya
20161206_avstraliya-i-okeaniya