Площадь квадрата

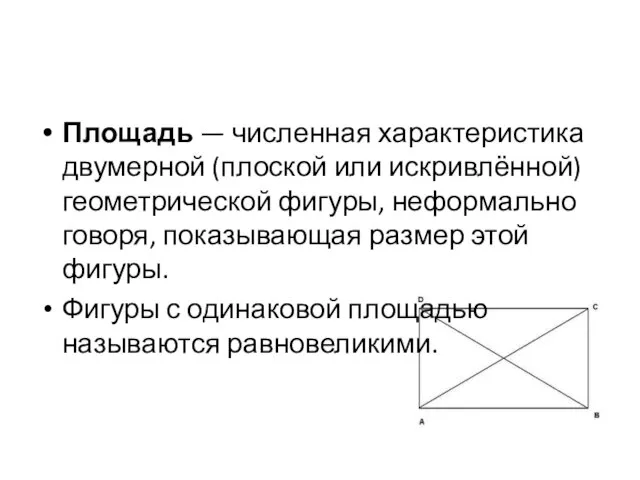
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры, неформально говоря, показывающая размер этой фигуры.
Фигуры с одинаковой площадью называются равновеликими.

Аксиомы площади
Площадь единичного квадрата равна 1.
Площадь аддитивна.
Площадь неотрицательна.
аддитивность площади означает, что площадь целого равен сумме …составляющих его частей.

Докажем, что площадь квадрата со стороной а равна а2.
1 случай.
а=1/n, где n- нат.число. Возьмем квадрат со стороной 1 и разобьем его на n2 равных квадратов, как на рисунке.
Так как площадь большого
квадрата равна 1, то площадь
каждого маленького
квадрата...

Сторона каждого маленького квадрата равна…, т.е. равна а. Итак, S= 1/n2 = (1/n)2 =a2 (1)
Случай 2.
Пусть теперь а представляет собой конечную десятичную дробь, содержащую n знаков после запятой, так же число а может быть целым, и тогда n=0. Тогда число квадратиков на каждой стороне m=а*10n . Разобьем данный квадрат со стороной а на m2 равных квадратов, как на рисунке.

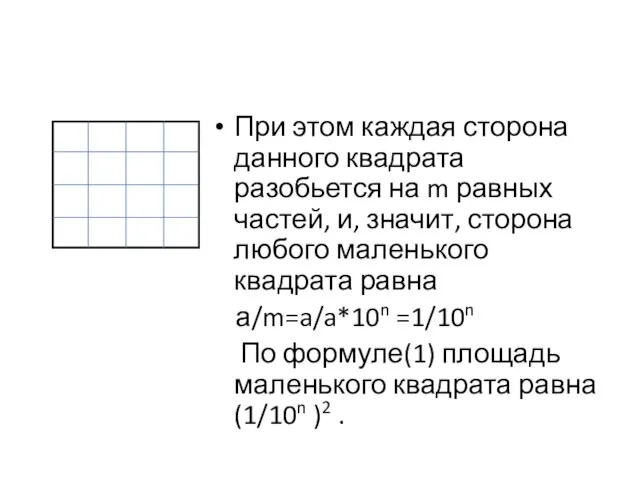
При этом каждая сторона данного квадрата разобьется на m равных частей, и, значит, сторона любого маленького квадрата равна
а/m=a/a*10n =1/10n
По формуле(1) площадь маленького квадрата равна (1/10n )2 .

Следовательно, площадь данного квадрата равна
m2 * (1/10n)2 =(m/10n)2= (a*10n/10n)2= a2 .
Пусть число а представляет собой бесконечную десятичную дробь. Рассмотрим число аn, получаемое из а отбрасыванием всех десятичных знаков после запятой, начиная с(n+1)-го. Так как число а отличается от аn не более чем на 1/10n, то аn ≤ а ≤ аn + 1/10n , откуда аn2 ≤ а2 ≤ (аn + 1/10n )2 . (2)

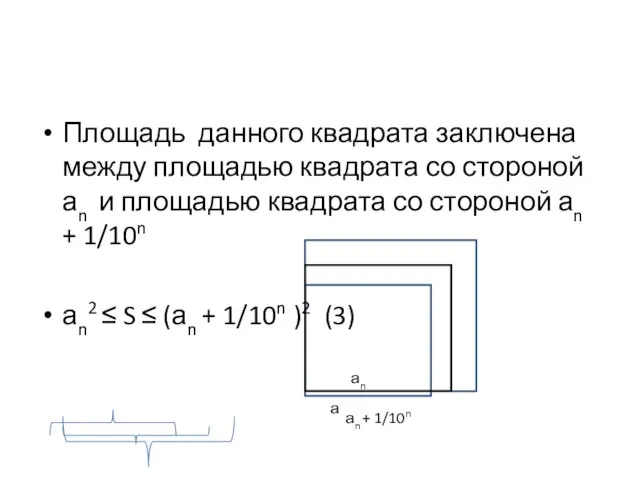
Площадь данного квадрата заключена между площадью квадрата со стороной аn и площадью квадрата со стороной аn + 1/10n
аn2 ≤ S ≤ (аn + 1/10n )2 (3)
а
аn + 1/10n
аn

Будем неограниченно увеличивать число n. Тогда число 1/10n , будет становиться сколь угодно малым, и, значит, число (аn + 1/10n )2 будет сколь угодно мало отличаться от числа аn2 . Поэтому из неравенств (2) и (3) следует, что число S сколь угодно мало отличается от числа а2 . Следовательно, эти числа равны: S= а2 , Ч.Т.Д.

Теорема Пифагора.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

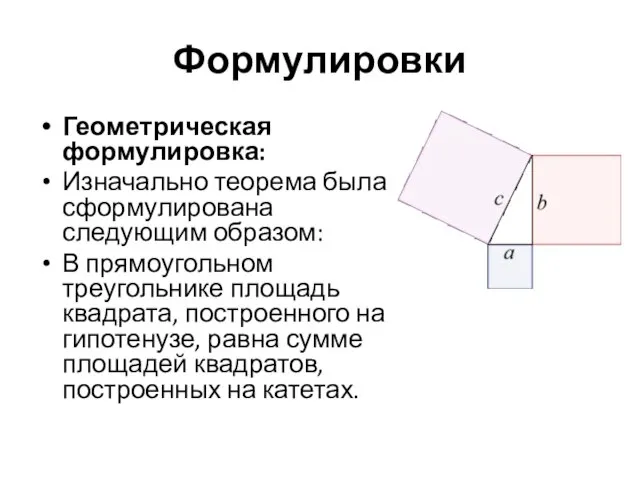
Формулировки
Геометрическая формулировка:
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:

Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.
Обратная теорема Пифагора:
Для всякой тройки положительных чисел a, b и c, такой, что a2 + b2 = c2, существует прямоугольный треугольник с катетами a и b и гипотенузой c.