Презентация на тему Кратные и Двойные интегралы

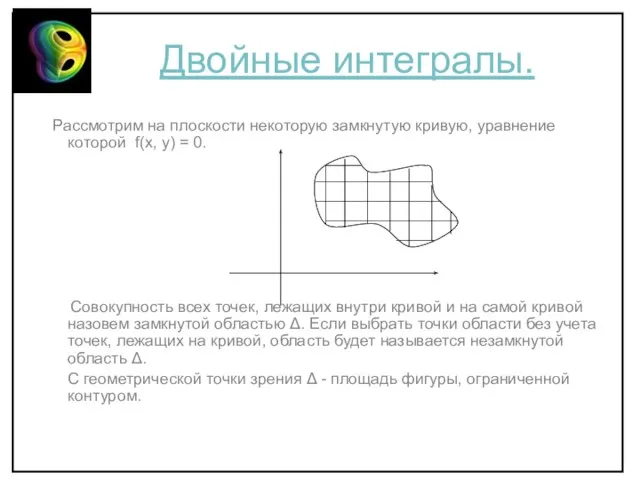
Двойные интегралы.
Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой f(x, y) = 0.
Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью Δ. Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область Δ.
С геометрической точки зрения Δ - площадь фигуры, ограниченной контуром.

Разобьем область Δ на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние , а по оси у – на . Вообще говоря, такой порядок разбиения необязателен, возможно разбиение области на частичные участки произвольной формы и размера.
Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны
В каждой частичной области возьмем произвольную точку и составим интегральную сумму
где f – функция непрерывная и однозначная для всех точек области Δ.
Если бесконечно увеличивать количество частичных областей Δi, тогда, очевидно, площадь каждого частичного участка Si стремится к нулю.

Определение
Если при стремлении к нулю шага разбиения области Δ интегральные суммы имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области Δ.
учетом того, что получаем:
В приведенной выше записи имеются два знака Σ, т.к. суммирование производится по двум переменным х и у.
Т.к. деление области интегрирования произвольно, также произволен и выбор точек , то, считая все площади одинаковыми, получаем формулу:

Условия существования двойного интеграла
Сформулируем достаточные условия существования двойного интеграла
Теорема. Если функция f(x, y) непрерывна в замкнутой области Δ, то двойной интеграл существует.

Теорема
Если функция f(x, y) ограничена в замкнутой области Δ и непрерывна в ней всюду, кроме конечного числа кусочно – гладких линий, то двойной интеграл существует.

Свойства двойного
интеграла.
1)
2)
3) Если Δ = Δ1 + Δ2, то
4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.
5) Если f(x, y) ≥ 0 в области Δ, то
6) Если f1(x, y) ≤ f2(x, y), то
7)

Вычисление двойного
интеграла
Теорема
Если функция f(x, y) непрерывна в замкнутой области Δ, ограниченной линиями х = a, x = b, (a < b), y = ϕ(x), y = ψ(x), где ϕ и ψ - непрерывные функции и
ϕ ≤ ψ, тогда

Теорема.
Если функция f(x, y) непрерывна в замкнутой области Δ, ограниченной линиями y = c, y = d (c < d), x = Φ(y), x = Ψ(y) (Φ(y) ≤ Ψ(y)), то

Замена переменных в двойном интеграле
Расмотрим двойной интеграл вида , где переменная изменяется в пределах от a до b, а переменная – от до
Положим
Тогда
;
; dy =
;

т.к. при первом интегрировании переменная принимается за постоянную, то
подставляя это выражение в записанное выше соотношение для , получаем:

Выражение называется определителем Якоби или Якобианом функций и
(Якоби Карл Густав Якоб – (1804-1851) – немецкий математик)
Тогда
Т.к. при первом интегрировании приведенное выше выражение для принимает вид ( при первом интегрировании полагаем ), то при изменении порядка интегрирования, получаем соотношение: