Презентация на тему Модели в механике. Система отчета. Траектория и длина пути.

Модели в механике. Система отсчета.
Траектория, длина пути, вектор перемещения
Простейшей формой движения является механическое движение. Оно заключается в изменении с течением времени положения тел или их частей друг относительно друга. В этой части курса будет изучаться движение двух модельных объектов - материальной точки и абсолютно твердого тела . Это делается для того, чтобы выявить наиболее общие закономерности механического движения.
Материальная точка - тело, размерами которого можно пренебречь по сравнению с расстояниями до других тел в данной задаче. Примерами такого объекта могут быть Земля при ее движении вокруг Солнца (но не для человека, находящегося на ее поверхности); молекула в разреженном газе.
Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению движения системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек.

Материальная точка, где же тебя разыскать?
Можно любое взять тело: слона, бегемота, кровать.
Только сравни для примера ты их размеры и путь.
Если тащу я пожитки, что уж, пора отдохнуть,
Значит, на том расстоянии я, словно точка, бреду.
Рост мой, размеры пожиток – с мусором здесь наряду.
Рад, что хоть массу считают. Был бы заряд, и его
Физики мне оставляют. Как я устал от всего!
Сделали точкой, смеются: “Вырасти хочешь, пацан?
Меньше возьми расстояние”. Вот такой простенький план.
Лишь в геометрии хуже, точка здесь слышит в ответ:
“Нет у тебя ни размеров, нет ничего! Нет и нет!”

При взаимодействии друг с другом тела могут деформироваться, т. е. изменять свою форму и размеры. В определенных случаях деформации тел можно не учитывать. Поэтому в механике вводится еще одна модель - абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не деформируется, т.е. расстояние между двумя его произвольными точками остается неизменным.

Как ясно из определения механического движения, необходимо определить тело отсчета, то есть то тело, относительно которого изучается движение. Кроме того, должна быть определена система координат, связанная с этим телом, и прибор для измерения времени.
Все это вместе называется системой отсчета. Примером такой системы отсчета может быть декартовая система координат с началом в некоторой точке и секундомер. Иногда в качестве системы координат выбирают сферическую или цилиндрическую.
Теперь мы можем однозначно определить положение тела в пространстве. Пусть материальная точка находилась в положении 1 и
переместилась в положение 2 . Линия, соединяющая точки, через которые проходило тело, называется траекторией, а ее длина
характеризует пройденный путь. Так как путь - это длина , то она не может быть отрицательной.
По характеру траектории движение можно разделить на два простейших вида: прямолинейное и движение по окружности. Из этак движений можно составить любое, даже очень сложное движение.

Длина траектории – путь,
А траектория – линия.
Ты это, дружок, не забудь.
Взгляни-ка на небо на синее.
Летит самолет. Видишь след?
Вот это – его траектория.
Длина ее, пусть, километр.
Путь найден. Простая теория.
Физика для детей

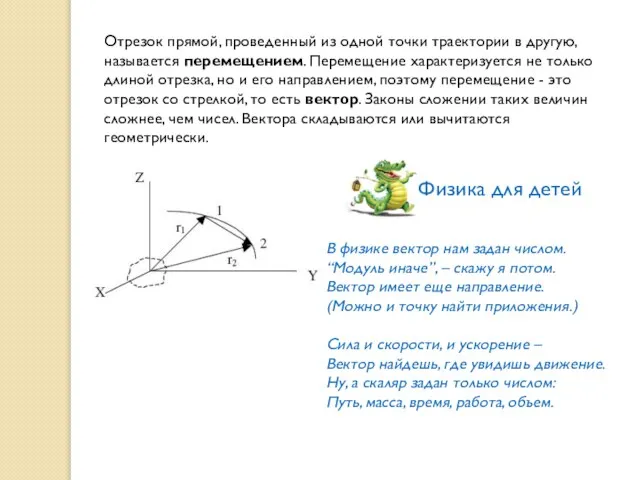
Отрезок прямой, проведенный из одной точки траектории в другую, называется перемещением. Перемещение характеризуется не только длиной отрезка, но и его направлением, поэтому перемещение - это отрезок со стрелкой, то есть вектор. Законы сложении таких величин сложнее, чем чисел. Вектора складываются или вычитаются геометрически.
В физике вектор нам задан числом.
“Модуль иначе”, – скажу я потом.
Вектор имеет еще направление.
(Можно и точку найти приложения.)
Сила и скорости, и ускорение –
Вектор найдешь, где увидишь движение.
Ну, а скаляр задан только числом:
Путь, масса, время, работа, объем.
Физика для детей

Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила.
Геометрически векторы изображаются направленными отрезками.
Вектор характеризуется следующими элементами:
1) начальной точкой (точкой приложения);
2 )направлением;
3) длиной («модулем вектора»).
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора A обозначается |A|
здесь вектора выделены жирным шрифтом - вместо стрелочки над буквой

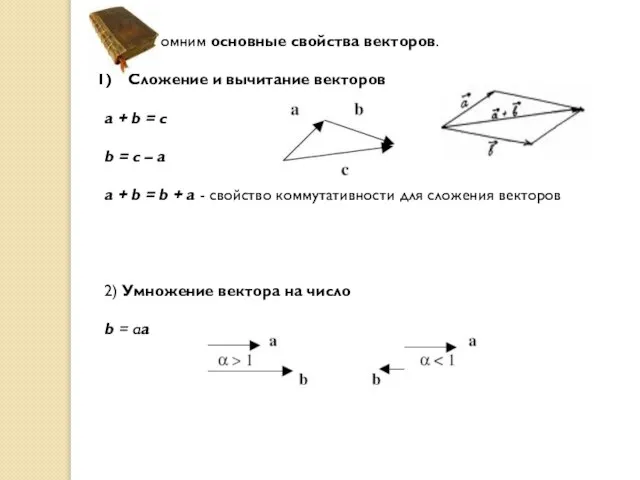
Вспомним основные свойства векторов.
Сложение и вычитание векторов
a + b = c
b = c – a
a + b = b + a - свойство коммутативности для сложения векторов
2) Умножение вектора на число
b = αa

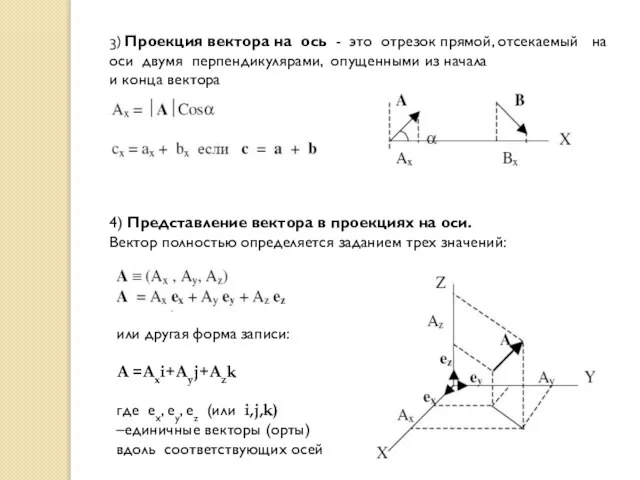
3) Проекция вектора на ось - это отрезок прямой, отсекаемый на оси двумя перпендикулярами, опущенными из начала
и конца вектора
4) Представление вектора в проекциях на оси.
Вектор полностью определяется заданием трех значений:
или другая форма записи:
A =Axi+Ayj+Azk
где ex, ey, ez (или i,j,k)
–единичные векторы (орты)
вдоль соответствующих осей

5) Скалярное произведение векторов.
В результате получается скаляр.
Свойства скалярного произведения
коммутативность :
ассоциативность :
A B=AxBx+AyBy+AzBz
6) Модуль вектора.
|A|=

7) Векторное произведение векторов А и В - это вектор, обозначаемый символом [AB] или A x B и определяемый формулой
где A и B - модули перемножаемых векторов, α - угол между векторами, n - единичный вектор нормали к плоскости в которой лежат векторы А и В. Направление n выбирается так, чтобы последовательность векторов A , B, n образовывала правовинтовую систему.
8) Радиус - вектор - вектор, проведенный из начала координат в точку,
в которой находится в данный момент движущееся тело. Его можно выразить в проекциях на оси:
Или в другой форме: r =x i+y j+z k

9) Если даны две точки пространства
A(a1 , a2 , a3) B(b1 , b2 , b3)
То :
- вектор AB имеет следующие координаты:
AB(a1 - b1 , a2 - b2 , a3 - b3)
- длину отрезка |AB| можно вычислить по формуле
|AB|=

Задание.
На оси Ox найти точку, равноудаленную от точек A(2;−4; 5) и B(−3; 2; 7).
Решение.
Пусть M - искомая точка. Для нее должно выполняться равенство |AM| =|MB|. Так как эта точка лежит на оси Ox, то ее координаты (x; 0; 0), а поэтому имеем
Отсюда после возведения в квадрат получим
(x − 2)2 + 41 = (x + 3)2 + 53 или 10x = −17, x= −1.7.
Таким образом, искомая точка имеет координаты (−1.7; 0; 0).

Задание.
Найти косинус угла между векторами AB и AC . Точки A,B,C заданы:
A(−4; 4;4), B(3;1;0), C(−1;0;6).
Решение.
Сначала найдем координаты векторов
AB=(3+4;1−4;0−4)=(7;−3;−4) ,
AC =(−1+4;0−4;6−4)= (3;−4;2) .
Найдем длины векторов:
|AB|=
|AC|=
Тогда косинус угла α между векторами AB и AC равен:
Cos α= (AB AC) / (|AB|| AC|)=

Движение материальной точки
При движении материальной точки ее координаты с течением времени изменяются.
В общем случае ее движение определяется скалярными уравнениями
x = x(t), y = y(t), z = z(t)
или эквивалентным векторным уравнением
r = r(t)
Эти уравнения называются кинематическими уравнениями движения материальной точки.
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Следовательно, если материальная точка движется в пространстве, то она обладает тремя степенями свободы (координаты х, у и z); если – в некоторой плоскости, то  двумя степенями свободы; если – вдоль прямой линии, то – одной степенью свободы.

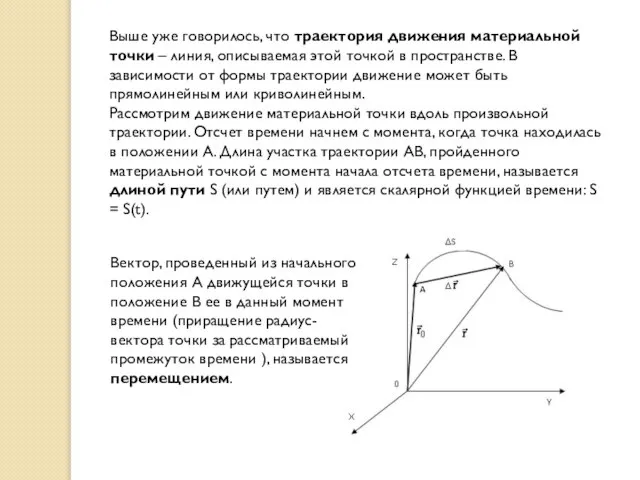
Выше уже говорилось, что траектория движения материальной точки – линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.
Рассмотрим движение материальной точки вдоль произвольной траектории. Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути S (или путем) и является скалярной функцией времени: S = S(t).
Вектор, проведенный из начального положения А движущейся точки в положение В ее в данный момент времени (приращение радиус-вектора точки за рассматриваемый промежуток времени ), называется перемещением.

Не думай, что просто судить о движении –
Здесь множество будет подводных камней.
Туман на реке, а ты принял решение,
Что все ж поплывешь куда надо по ней.
И вот, ты в тумане – исчезло движенье,
Ведь сравнивать не с чем: “Вы где, берега?
Нет тела отсчета – терплю пораженье –
Любое мне дайте, туман и река!”
И вижу вдруг снова и берег, и лодки.
Березку что ль выбрать? Иль плотик вдали?
Но вновь не понять, хоть собрал я все сводки,
Березки проплыли всей рощей мои,
А плотик злосчастный как был – в километре!
Гвоздями прибили там, что ли, его?
Ведь вместе мы мчались с рекою и ветром!
Где скорость моя? Не пойму ничего.
“Зависит, балбес, всё от тела отсчёта,
Того, что ты выбрал, – сказали друзья, –
Ты делай для каждого тела расчёты.
Пусть разные числа. Не бойся их зря”.
Физика для детей

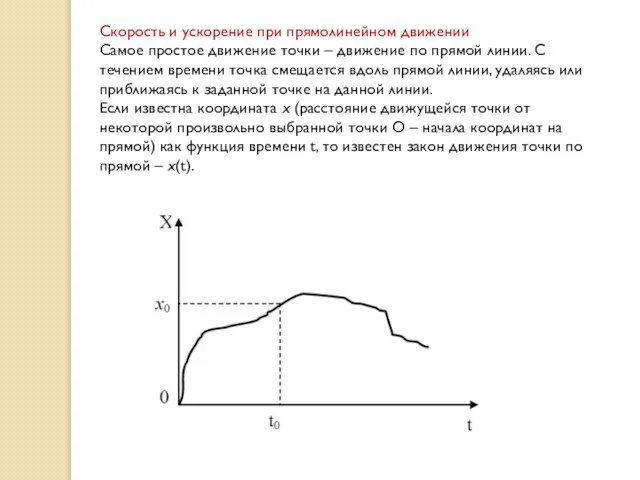
Скорость и ускорение при прямолинейном движении
Самое простое движение точки – движение по прямой линии. С течением времени точка смещается вдоль прямой линии, удаляясь или приближаясь к заданной точке на данной линии.
Если известна координата х (расстояние движущейся точки от некоторой произвольно выбранной точки О – начала координат на прямой) как функция времени t, то известен закон движения точки по прямой – х(t).

Путь, пройденный точкой, можно определить по ее координате только в том случае, если точка движется в одном направлении. Зависимость координаты от времени х(t) полностью определяет движение точки по прямой, однако в механике важно знать еще две величины: скорость и ускорение.
Скорость точки есть физическая величина, определяющая изменение координаты с течением времени. Величина средней скорости численно равна отношению пройденного точкой расстояния ко времени, за которое это расстояние пройдено. Пусть в момент времени t1 тело было в точке х1 ,а в момент t2 – в точке х2. Следовательно, перемещение его равно х = х2  х1 тогда средняя скорость равна:
Скорость так определи:
Путь на время раздели.
“Метр в секунду” – единица.
Как легко всем обучиться!
Физика для детей
Физика для детей

Очевидно, что средняя скорость зависит от промежутка времени, за который мы ее определяем. Если средняя скорость для любого промежутка времени при данном движении одинакова, то это движение происходит с постоянной скоростью и называется равномерным движением.
На графике зависимости координаты от времени х(t) равномерное движение представляется прямой линией. При равномерном движении от начала координат нет разницы между величиной координаты и величиной пути.
Вот равномерное движенье:
Когда ты равные пути
За так же равные мгновенья
Сумел проехать иль пройти.
Физика для детей

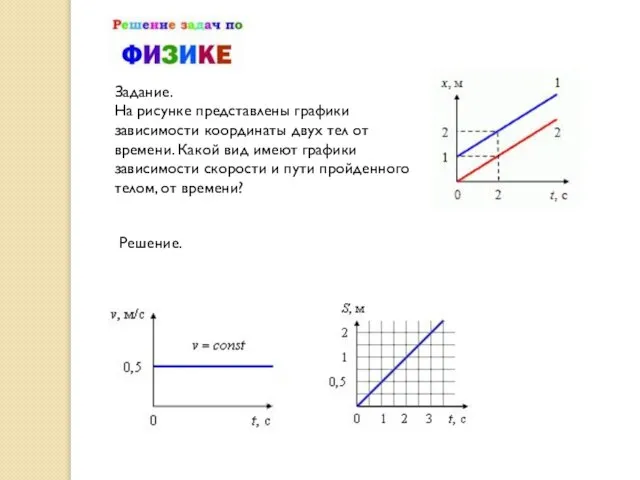
Задание.
На рисунке представлены графики зависимости координаты двух тел от времени. Какой вид имеют графики зависимости скорости и пути пройденного телом, от времени?
Решение.

При неравномерном движении средняя скорость будет различной в зависимости от того, за какой промежуток времени мы ее определяем. Поэтому для более полной и точной характеристики движения вводят мгновенную скорость, т.е. скорость точки в данный момент времени t. По определению мгновенная скорость равна пределу:
В математике этот предел называется производной координаты х по времени t и обозначается:

Расстояние, пройденное точкой за промежуток времени t2t1 при постоянной скорости v0, очевидно равно произведению скорости v0 на время t2t1:
х2  х1= v0(t2  t1).
При непостоянной скорости движения точки это выражение лишено смысла.
В случае, когда средняя скорость неизвестна, вычисление расстояния (пути), пройденного телом, нужно производить особым способом, основанным на том, что всякое движение за достаточно малый промежуток времени можно всегда с достаточной точностью полагать равномерным. Поэтому для определения расстояния dx, которое пройдет тело за достаточно малый промежуток времени dt, нужно скорость v в данный момент времени t умножить на соответствующее приращение времени dt:
dx = v dt

Предположим, что мы разбили весь промежуток времени t2t1 на бесконечно большое число малых промежутков dt. Каждому малому промежутку dt соответствует свое малое приращение dx.
Расстояние х2х1, пройденное за время t2t1, можно записать в виде суммы всех dx. Такая сумма называется интегралом и записывается в виде:
Вместо dx под знаком интеграла подставим равную ему величину v dt, и будем суммировать по времени от t1 до t2. Тогда отрезок, пройденный телом за время t2t1, можно записать в такой форме:

При неравномерном движении точка имеет переменную скорость, которую, подобно координате, можно рассматривать как функцию времени v(t). На быстроту изменения скорости указывает величина ускорения. Ускорением материальной точки а называют величину, численно равную производной скорости по времени:
Ускорение также является второй производной координаты х по времени

Движение с постоянным ускорением называется равнопеременным. В этом случае зависимости координаты х и скорости v от времени даются уравнениями:
где х0 называется начальной координатой (значение координаты х в начальный момент времени t=0), v0 – начальной скоростью.
Здесь v0 и а – алгебраические выражения, т.е. v00 и а0, если векторы скорости и ускорения направлены в сторону положительной полуоси OХ, и v00 и а0 – в противном случае.

Задание.
В 10:00 туристы на лодке поплыли из пункта А вниз по течению реки. Пройдя 12 километров, туристы остановились для отдыха на 3 часа. Затем они вернулись в пункт А в 18:00. Определить (в км/ч) собственную скорость лодки, если скорость течения реки 1 км/ч.
Решение.
Пусть х – собственная скорость лодки.
Тогда
х+1 – скорость движения лодки по течению,
х-1 – скорость движения лодки против течения.
Далее,
12/(х+1) – время движения лодки по течению.
12/(х-1) – время движения лодки против течения.
Общее время движения:
Отсюда х = 5(км/ч).

Задание.
Даны уравнения движения тела: x = vxt и y = yo + vyt.
Запишите уравнение траектории и постройте ее график, если
vx = 0,25 м/с,
vy = 1 м/с,
yo = 0,2 м.
Решение.
Решая совместно уравнения x = vxt и y = yo+vyt, исключим время t и
получим уравнение траектории:
y = 0.2 + 4x.

Задание.
Пассажир едет в поезде, скорость которого 80 км/ч.
Навстречу этому поезду движется товарный поезд
длиной 1 км со скоростью 40 км/ч.
Сколько времени товарный поезд будет двигаться
мимо пассажира?
Решение.
1-й способ.
Cистему отсчета свяжем с Землей. Наблюдатель находится в точке O с координатой x = 0. Координата хвоста товарного поезда L = 1 км. Уравнения движения обоих тел имеет вид:
x1 = v1t (пассажир) ; x2 = L − v2t (хвост товарного поезда)
В момент встречи хвоста поезда с пассажиром x1 = x2 или v1t = L − v2t Отсюда время встречи равно
t=L / (v1+v2) = 30 (с).
2-й способ.
Свяжем систему координат с товарным поездом, тогда скорость пассажира в поезде, по отношению к неподвижной системе координат (товарный поезд), равна vo=v1+v2. Так как длина поезда L, то пассажир проедет мимо него, следовательно, и будет наблюдать его, в течение времени
t=L / (v1+v2) = 30 (с).

Задание.
Буратино и Пьеро бежали наперегонки. Пьеро весь путь бежал с одной и той же скоростью, а Буратино первую половину пути бежал вдвое быстрее, чем Пьеро, а вторую половину — вдвое медленней, чем Пьеро. Кто победил?
Решение.
На вторую половину пути Буратино потратил ровно столько времени, сколько Пьеро на весь путь. А ведь сколько-то времени у Буратино ушло и на первую половину пути. Так что победил Пьеро.

Задание.
Если Аня идёт в школу пешком, а обратно едет на автобусе, то всего на дорогу она тратит 1,5 ч. Если же она едет на автобусе в оба конца, то весь путь у неё занимает 30 мин. Сколько времени потратит Аня на дорогу, если и в школу и из школы она будет идти пешком?
Решение.
Путь в оба конца на автобусе занимает 30 мин, следовательно, путь в один конец на автобусе займёт 15 мин.
На дорогу в один конец пешком понадобится 1,5 часа - 15 мин, т.е. 1 час 15 мин. Значит, на дорогу пешком в оба конца Аня тратит 2, 5 ч.

Задание.
Первую половину пути автомобиль проехал со скоростью v1 = 60 км/ч, а вторую — со скоростью v2 = 40 км/ч. Определить среднюю скорость V автомобиля на всем пути.
Решение:
Первую половину пути автомобиль проехал со скоростью 60 км/ч и затратил время, равное
t1=(S/2) / v1
Вторую половину пути автомобиль проехал со скоростью 40 км/ч и затратил время, равное
t2=(S/2) / v2
По определению, средняя скорость Vср при равномерном прямолинейном движении равна отношению всего пройденного пути ко всему затраченному времени:
Vср = S / (t1 + t2)=2 v1 v2 /(v1 + v2)= 48 (км/ч)