Презентация на тему Молекулярно-кинетическая теория идеальных газов

7. Молекулярно-кинетическая теория идеальных газов
7.1. Статистический и термодинамический методы исследования
Молекулярная физика и термодинамика — разделы физики, в которых изучаются зависимости свойств тел от их строения, взаимодействия между частицами и характера движения частиц.
Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений.
Основа молекулярной физики — это представление, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.
Явления в молекулярной физике изучаются с помощью статистического метода.
Статистический метод – это метод исследования систем, состоящих из большого числа частиц и использующий статистические закономерности динамических характеристик этих частиц (скорости, энер­гии и т. д.).

Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, а также процессы перехо­да между этими состояниями.
Явления термодинамики изучаются с помощью термодинамического метода.
Термодинамический метод – это метод исследования систем, состоящих из большого числа частиц и использующий величины, характеризующие систему в целом (давление, объем, температура).
Состояние системы задает­ся термодинамическими параметрами (параметрами состояния) —температурой, давлением и удельным объемом.
Термодинамика имеет дело с термодинамической системой.
Термодинамическая система – это совокупность мак­роскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой).

Температура — физическая величина, харак­теризующая состояние термодинамического равновесия макроскопической системы. В настоящее время применяются только две температурные шкалы — термодина­мическую и Международную практическую.
В Международной практической шкале тем­пература измеряется в градусах Цельсия (°С).
Температура замерзания и кипения воды при давлении 1,013⋅105 Па соответственно 0 и 100°С (реперные точки).
В термодинамической шкале тем­пература измеряется в кельвинах (К).
Температура определяется по одной реперной точке — тройная точка воды (температура, при которой лед, вода и насыщенный пар при давления 609 Па находятся в термодинамическом равновесии).
Температура этой точки по термодинамической шкале равна 273,15К.

Термодинамическая температура и температура по Между­народной практической шкале связаны соотношением:
Т = 273,15 + t.
Нормальные условия:
Удельный объем v — это объем единицы массы.
Когда тело однородно, т. е. его плотность ρ = const, то v=V/m=1/ ρ.

7.2. Законы, описывающие поведение идеальных газов
В молекулярно-кинетической теории пользуются моделью идеаль­ного газа, согласно которой считают, что:
1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

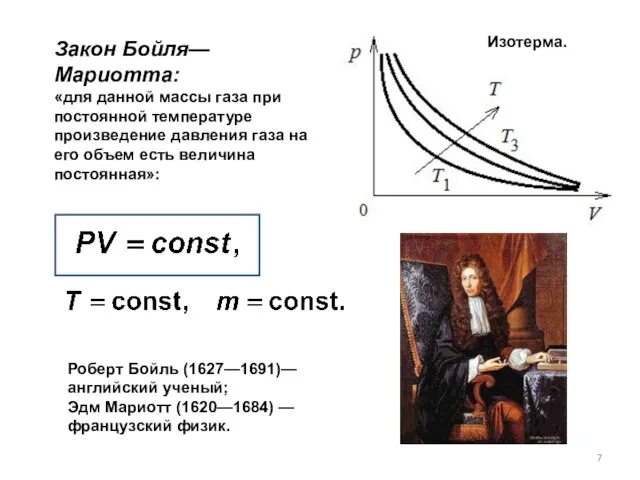
Изотерма.
Закон Бойля—Мариотта:
«для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная»:
Роберт Бойль (1627—1691)—английский ученый;
Эдм Мариотт (1620—1684) — французский физик.

Законы Гей-Люссака
1) объем данной массы газа при постоянном давлении изменяется линейно с температурой:
Жозеф Гей-Люссак (1778—1850) — французский ученый.
Процесс, протекающий при постоянном давлении, называется изобарным.
Изобара.

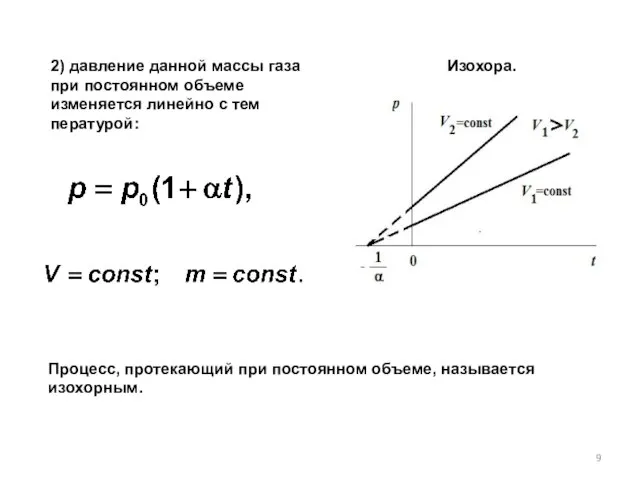
2) давление данной массы газа при постоянном объеме изменяется линейно с тем­пературой:
Процесс, протекающий при постоянном объеме, называется изохорным.
Изохора.

В термодинамической шкале температур:

Закон Авогадро:
«моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы».
А. Авогадро (1776—1856) — итальянский физик и химик.
При нормальных условиях этот объем равен 22,41⋅10–3 м3/моль (молярный объем).

Моль – единица количества вещества, количество вещества системы, содержащей столько же структурных элементов, сколько содержится в 0,012 кг изотопа углерода.
В одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро:
Молярная масса:
– это масса одного моля вещества.

Закон Дальтона:
«давление смеси идеальных газов равно сумме парциальных давлений p1, p2 ,..., рn входящих в нее газов»:
Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
Дж. Дальтон (1766—1844) — английский химик и физик.

7.3. Уравнение состояния идеального газа
(Менделеева-Клапейрона)
Уравнением состояния термодинамической системы называется уравнение, которое связывает давление р, объем V и температуру Т:
Французский физик и инженер Бенуа Клапейрон (1799—1864).
Русский ученый Дмитрий Иванович Менделеев (1834—1907)

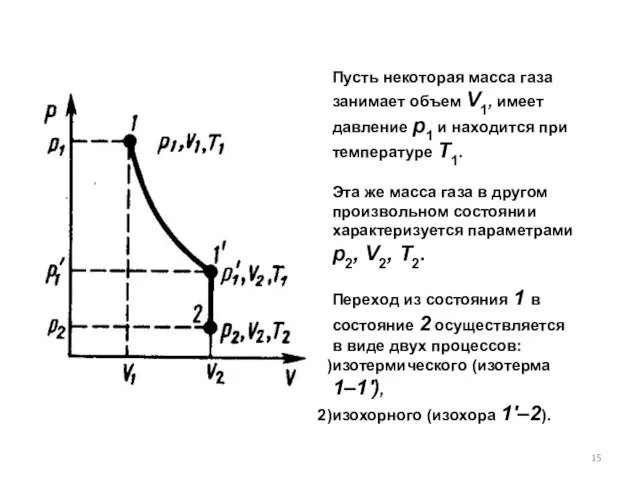
Пусть некоторая масса газа занимает объем V1, имеет давление р1 и находится при тем­пературе T1.
Эта же масса газа в другом произвольном состоянии характеризуется параметрами р2, V2, T2.
Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов:
изотермического (изотерма 1–1'),
изохорного (изохора 1'–2).

В соответствии с законами Бойля — Мариотта и Гей-Люссака за­пишем:
Исключив из уравнений
получим:
— уравнением Клапейрона, в котором В — газовая постоянная, различная для разных газов.

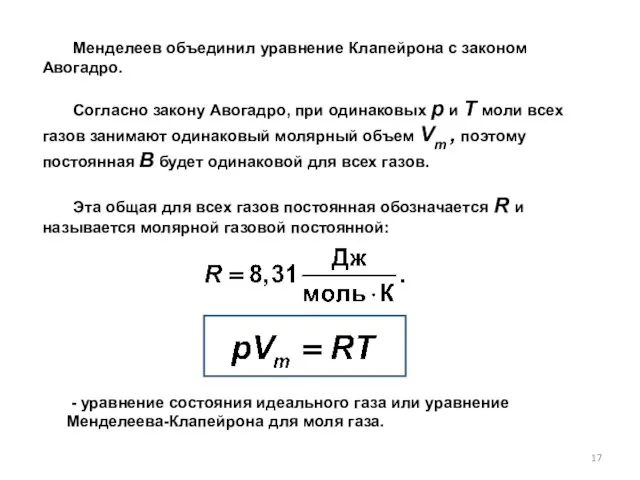
Менделеев объединил уравнение Клапейрона с законом Авогадро.
Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем Vm , поэтому постоянная В будет одинаковой для всех газов.
- уравнение состояния идеального газа или уравнение
Менделеева-Клапейрона для моля газа.
Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной:

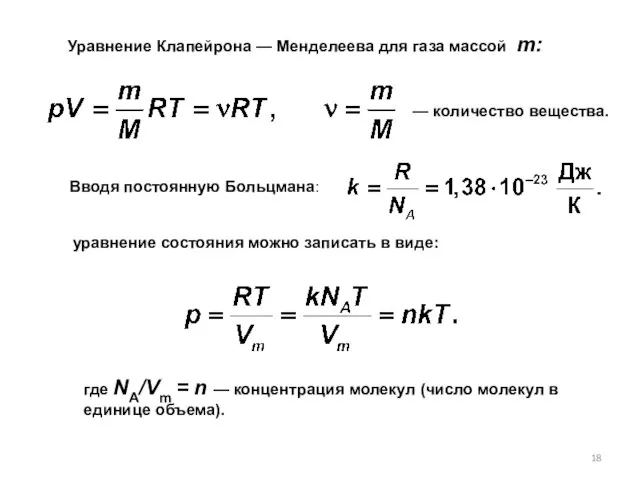
Уравнение Клапейрона — Менделеева для газа массой т:
— количество вещества.
Вводя постоянную Больцмана:
уравнение состояния можно записать в виде:
где NA/Vm = n — концентрация молекул (число молекул в единице объема).

Число молекул, содержащихся в 1 м3 газа при нормальных условиях, называется числом Лошмидта:
1. Давление идеального газа при данной температуре прямо пропорциональ­но концентрации его молекул (или плотности газа).
2. При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул.
В результате можно сделать выводы:
Иоганн Лошмидт (1821-1895) — австрийский физик и химик, член Австрийской академии наук.

7.4. Основное уравнение молекулярно-кинетической теории идеальных газов
Пусть в сосуде объемом V находится идеальный газ массой m с числом молекул N каждая из которых имеет массу m0 и скорость v. Концентрация молекул в газе n=N/V.
Выделим на стенке сосуда некоторую элементарную площадку ΔS и вычислим давление, оказываемое на эту площадку.
При каждом соударении молеку­ла, движущаяся перпендикулярно площадке, передает ей импульс:
m0v – (– m0v) = 2m0v,
m0 — масса молекулы,
v — ее скорость.

За время dt площадке dS передается импульс dP. Тогда давление газа, оказываемое на стенку сосуда, будет равно:
Хаотическое движение молекул происходит вдоль трех взаимно перпендикулярных направлений. Вдоль каждого из них движется 1/3 молекул.
Половина молекул 1/6 движется вдоль данного направления в одну сторону, половина — в противоположную.
Тогда число ударов молекул, движущихся в заданном направлении, о площадку ΔS будет 1/6 n ΔSv Δt.
При столкновении с площадкой эти молекулы передадут ей импульс:

Давление газа, оказываемое им на стенку сосуда:
Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2, ..., vN, то целесообразно рассматривать среднюю квадратную скорость:
Тогда основное уравнение молекулярно-кинетической те­ории идеальных газов примет вид:

Другие формы этого уравнения :
1. Учитывая, что n =N / V, получим
2. Так как масса газа m=Nm0, то уравнение можно переписать в виде:
3. Для одного моля газа т=М (М — молярная масса):

Используя уравнение Клапейрона — Менделеева получим:
Так как M=m0NА,
т0 — масса одной молекулы,
NА — постоянная Авогадро, то:
k=R/NА — постоянная Больцмана.