Содержание
- 2. ЛИТЕРАТУРА: 1. Брюшинкин В.Н. Логика: Учебник. – 3-е изд. – М.: Гардарики, 2001. С. 181-247. 2.
- 3. 1. ПОНЯТИЕ И ВИДЫ СИЛЛОГИЗМОВ Силлогизм – это дедуктивное умозаключение, в котором вывод совершается на основе
- 4. Понятие и виды силлогизмов Все эпузы гантируются. Все фемины – эпузы. Следовательно, все фемины гантируются. Логика
- 5. Понятие и виды силлогизмов Силлогизмы Непосредственные Опосредованные Логика Силлогизмы
- 6. Понятие и виды силлогизмов Непосредственные силлогизмы – это силлогизмы, в которых вывод совершается из одной посылки.
- 7. Понятие и виды силлогизмов Опосредованные силлогизмы – это силлогизмы, в которых вывод совершается из двух или
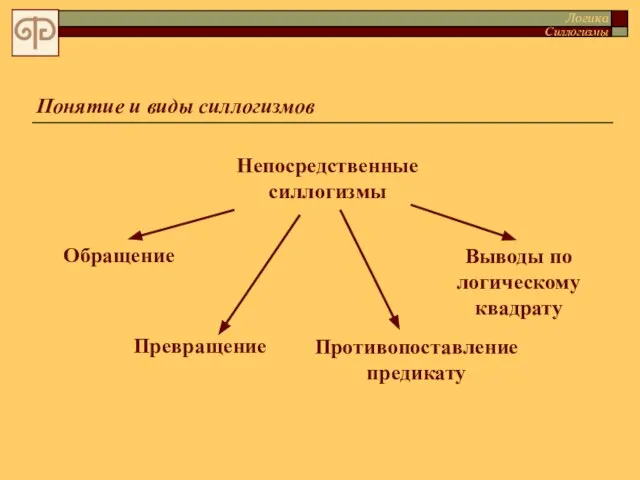
- 8. Непосредственные силлогизмы Обращение Превращение Противопоставление предикату Выводы по логическому квадрату Понятие и виды силлогизмов Логика Силлогизмы
- 9. Понятие и виды силлогизмов Опосредованные умозаключения Простой категорический силлогизм Полисиллогизм Логика Силлогизмы
- 10. 2. НЕПОСРЕДСТВЕННЫЕ УМОЗАКЛЮЧЕНИЯ Превращение – это силлогизм, состоящий в преобразовании категорического суждения в противоположное по качеству
- 11. Непосредственные умозаключения Логика Силлогизмы А├ Е, Е├ А, О├ I, I├ O Превращение
- 12. Непосредственные умозаключения Логика Силлогизмы
- 13. Обращение - непосредственный силлогизм, состоящий в преобразовании категорического суждения в суждение, субъектом которого является предикат исходного
- 14. Простое обращение – это обращение, при котором не изменяется количество исходного суждения. Непосредственные умозаключения Е├ Е,
- 15. Непосредственные умозаключения Обращение с ограничением – это обращение, при котором изменяется количество исходного суждения. А├ I
- 16. Противопоставление предикату – непосредственный силлогизм, состоящий в преобразовании суждения, в результате которого субъектом становится понятие, противоречащее
- 17. Непосредственные умозаключения Логика Силлогизмы
- 18. Д. Умозаключения по логическому квадрату: Непосредственные умозаключения выводы на основании отношения подчинения; выводы на основании отношения
- 19. Непосредственные умозаключения Выводы на основании отношения подчинения: а) Умозаключения от истинности к истинности. А├ I, E├
- 20. Непосредственные умозаключения б) Умозаключение от ложности к ложности. I ├А,O├E Логика Силлогизмы
- 21. Непосредственные умозаключения Выводы на основании отношения дополнительности: I├ О,O├ I Логика Силлогизмы
- 22. Непосредственные умозаключения Выводы на основании отношения противоречия: а) Умозаключения от ложности к истинности А├ О,O├ А,Е├
- 23. Непосредственные умозаключения б) Умозаключение от истинности к ложности А├О, O├А, Е├I, I├E Логика Силлогизмы
- 24. Непосредственные умозаключения Выводы на основании отношения противоположности: А├Е, Е├А Логика Силлогизмы
- 25. 3. ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ. ФИГУРЫ И МОДУСЫ Простой категорический силлогизм – дедуктивное умозаключение, в котором из
- 26. Простой категорический силлогизм Логика Силлогизмы Все политики – эгоисты. Все президенты – политики. Все президенты –
- 27. Простой категорический силлогизм Посылки силлогизма – суждения, из которых выводится новое суждение. Логика Силлогизмы
- 28. Простой категорический силлогизм Заключение силлогизма –новое суждение, которое выводится из посылок. Логика Силлогизмы
- 29. Простой категорический силлогизм Термины данного силлогизма – понятия, которые входят в посылки или заключение силлогизма. Логика
- 30. Простой категорический силлогизм Субъект заключения называется меньшим термином. Логика Силлогизмы
- 31. Простой категорический силлогизм Предикат заключения называется бóльшим термином. Логика Силлогизмы
- 32. Простой категорический силлогизм Термин, который встречается в посылках, но не встречается в заключении, называется средним термином.
- 33. Непосредственные умозаключения Все M есть P Все S есть M Все S есть P Логика Силлогизмы
- 34. Простой категорический силлогизм Суждение, в которое входит больший термин, называется бóльшей посылкой. Логика Силлогизмы
- 35. Простой категорический силлогизм Суждение, в которое входит меньший термин, называется меньшей посылкой. Логика Силлогизмы
- 36. Простой категорический силлогизм Содержание силлогизма – это понятия, встречающиеся в нём в качестве терминов. Логика Силлогизмы
- 37. Простой категорический силлогизм Форма силлогизма – это связь, которая придается терминам. Логика Силлогизмы
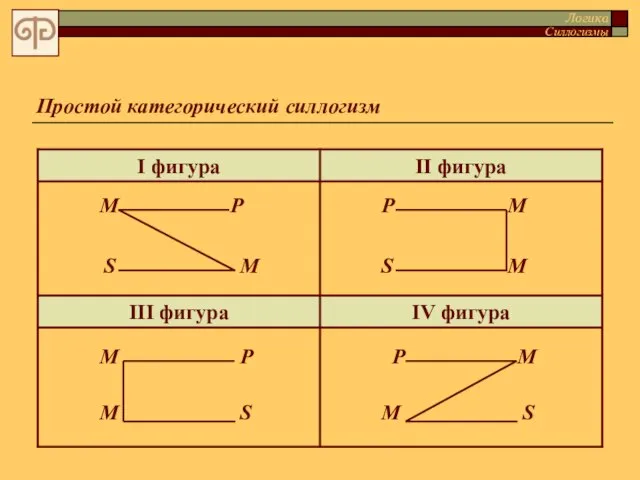
- 38. Простой категорический силлогизм Фигура силлогизма – множество силлогизмов, характеризуемое одинаковым положением среднего термина. Логика Силлогизмы
- 39. Простой категорический силлогизм М Р S М М Р S М М Р S М М
- 40. Простой категорический силлогизм Модус – разновидность силлогизма, характеризуемая определенной последовательностью категорических суждений. Логика Силлогизмы
- 41. Простой категорический силлогизм Модусов силлогизмов 256 Логика Силлогизмы
- 42. Простой категорический силлогизм Модус правилен, если не может быть так, что обе посылки истинны, а заключение
- 43. Простой категорический силлогизм Правильных модусов – 24 Нетривиальных правильных модусов – 19 Логика Силлогизмы
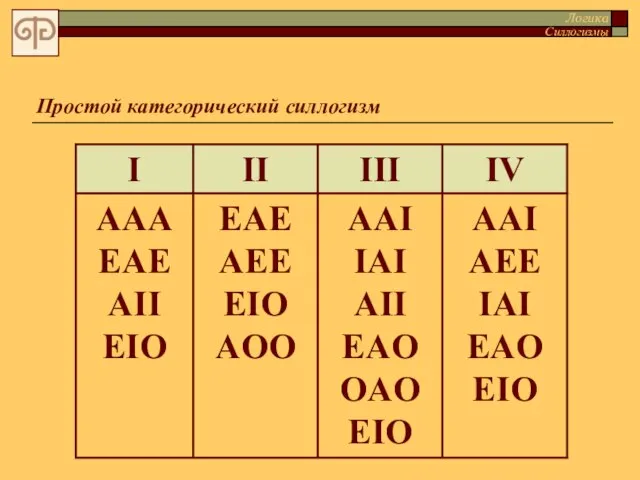
- 44. Простой категорический силлогизм Логика Силлогизмы
- 45. Простой категорический силлогизм Barbara, Celarent, Darii, Ferioque prioris; Cesare, Camestres, Festino, Baroko, sekundae; Tertia Darapti, Disamis,
- 46. 4. СПОСОБЫ ПРОВЕРКИ ПРАВИЛЬНОСТИ СИЛЛОГИЗМОВ Три способа проверки правильности силлогизмов: построение круговых схем для посылок и
- 47. Способы проверки правильности силлогизмов 1) Построение круговых схем для посылок и совмещение их на одной схеме
- 48. Все философы понимают Аристотеля Никто из присутствующих не понимает Аристотеля Никто из присутствующих не является философом.
- 49. Бóльшая посылка: Все философы (P) понимают Аристотеля (M). Р М Логика Силлогизмы
- 50. Меньшая посылка: Никто из присутствующих (S) не понимает Аристотеля (M). S М Логика Силлогизмы
- 51. Р М S Совмещаем схемы для большей и меньшей посылки: Логика Силлогизмы Согласно этой схеме, заключение
- 52. Все юристы знают признаки преступления. Все присутствующие знают признаки преступления. Все присутствующие являются юристами. Все P
- 53. Бóльшая посылка: Все юристы (P) знают признаки преступления (M). Р М Логика Силлогизмы
- 54. Меньшая посылка: Все присутствующие (S) знают признаки преступления (M). S М Логика Силлогизмы
- 55. Совмещаем схемы для бóльшей и меньшей посылки: 1-ый вариант Логика Силлогизмы S P М Согласно этой
- 56. Совмещаем схемы для бóльшей и меньшей посылки: 2-ой вариант Логика Силлогизмы S P М Согласно этой
- 57. Силлогизм является правильным, если нельзя построить такую совмещенную круговую схему, на которой обе посылки являются истинными,
- 58. 2) Обнаружение и предъявление контрпримера Способы проверки правильности силлогизмов Логика Силлогизмы
- 59. Контрпример – силлогизм, тождественный с данным по форме, но абсурдный по смыслу. Способы проверки правильности силлогизмов
- 60. Тождественный с данным по форме = имеющий ту же фигуру и тот же модус. Способы проверки
- 61. Все философы знают о Фалесе. Все присутствующие знают о Фалесе. Все присутствующие являются философами. Способы проверки
- 62. Все зулусы – люди. Все присутствующие – люди. Все присутствующие – зулусы. Контрпример: Способы проверки правильности
- 63. 3) Проверка на соответствие общим правилам силлогизма и правилам фигур Способы проверки правильности силлогизмов Логика Силлогизмы
- 64. Правила терминов: ПТ1. Во всяком силлогизме должно быть ровно три термина. ПТ2. Средний термин должен быть
- 65. Правила посылок: ПП1. Во всяком силлогизме должно быть ровно три категорических суждения. ПП2. Из двух отрицательных
- 66. Правила фигур: I фигура. В умозаключениях по первой фигуре меньшая посылка должна быть утвердительной, а бóльшая
- 67. 5. ЭНТИМЕМЫ Энтимема (греч. en tyme – в уме) – умозаключение, в котором опущена одна из
- 68. Силлогизм по I фигуре: Все пороки заслуживают наказания. Курение – это порок. Курение заслуживает наказания. Логика
- 69. 1) С опущенной бóльшей посылкой: “Курение заслуживает наказания, потому что оно – порок». 2) С опущенной
- 70. Силлогизм по II фигуре: Логика Силлогизмы Механизм образования энтимем
- 71. 1) С опущенной бóльшей посылкой: “Ни один политик не является честным человеком, поскольку ни один политик
- 72. Энтимемы Восстановление силлогизма до полной формы из энтимемы – операция, обратная операции построения энтимемы. Логика Силлогизмы
- 73. Определение пропущенного элемента силлогизма: посылки или заключения. Определение терминов, которые должны встречаться в полном силлогизме: среднего
- 74. Пример: “Рабов не следует держать в неволе, потому что они люди”. Энтимемы “Ни один раб не
- 75. Заключение силлогизма – суждение, предшествующее словам “потому что”; поскольку во втором суждении фигурирует термин “рабы”, являющийся
- 76. Термины силлогизма: “рабы” – меньший термин, “существо, которое следует держать в неволе” – бóльший термин, а
- 77. Полное умозаключение возможно по I или II фигуре. Тогда средний термин: в I фигуре – субъект
- 78. Большая посылка во II фигуре: “Ни одно из существ, которых следует держать в неволе, не является
- 79. Бóльшая посылка в I фигуре: “Ни один человек не есть существо, которое следует держать в неволе”
- 80. Силлогизм по I фигуре: Энтимемы Логика Силлогизмы
- 81. Если вернуться к формам естественного языка, полное умозаключение будет выглядеть так: Энтимемы Логика Силлогизмы
- 82. Более сложный пример восстановления энтимемы дает нам рассуждение Макиавелли из “Князя”: “Новый правитель всегда оказывается хуже
- 83. Термина, объединяющего заключение и посылку, нет. Это означает, что энтимема представляет собой сокращение двух силлогизмов. То,
- 84. Слово “всегда” означает, что мы имеем дело с общеутвердительными суждениями: “Все новые правители хуже старых”, “Все
- 85. Тогда первый силлогизм примет следующую форму: Энтимемы Логика Силлогизмы
- 86. Во втором силлогизме мы уже имеем заключение “Все новые правители хуже старых” и меньшую посылку “Все
- 87. Отсюда получается следующий силлогизм: Энтимемы Логика Силлогизмы
- 88. Мы теперь наглядно можем представить ход мысли Макиавелли в полной форме, в виде последовательности правильных умозаключений.
- 89. Это суждения: “Все новые правители – завоеватели” и “Все правители, которые притесняют своих подданных, хуже старых
- 90. Теперь мы в силах заметить, что первое суждение является ложным, поскольку мы можем представить и другие
- 91. Второе суждение, может быть, и не ложное, но несколько парадоксальное, поскольку в число тех правителей, которые
- 92. Восстановление энтимемы до полной формы помогло нам обнаружить ошибку, которую допустил Макиавелли. В этом главный практический
- 93. 6. ПОЛИСИЛЛОГИЗМЫ Сложный силлогизм, или полисиллогизм – последовательность простых силлогизмов, в которой заключение предшествующего силлогизма становится
- 94. Использование полисиллогизма позволяет построить логическую модель более сложных рассуждений, чем те, что могут быть смоделированы при
- 95. В полисиллогизме: Силлогизм, предшествующий другому силлогизму в последовательности силлогизмов, называется просиллогизмом. Силлогизм, следующий за другим силлогизмом
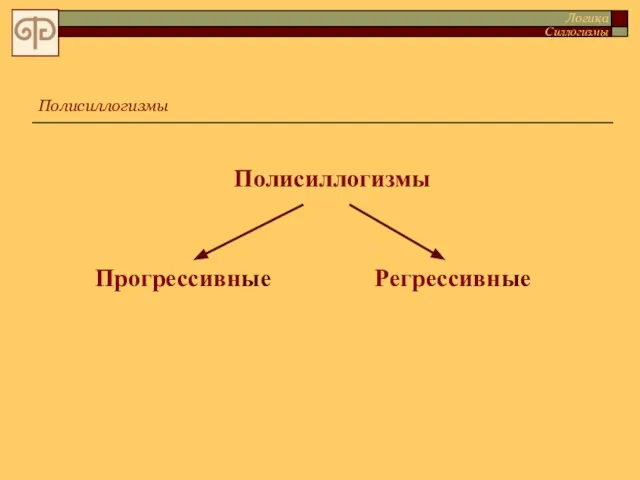
- 96. Полисиллогизмы Логика Силлогизмы Полисиллогизмы Прогрессивные Регрессивные
- 97. Прогрессивным называется полисиллогизм, в котором заключение просиллогизма становится большей посылкой эписиллогизма. Полисиллогизмы Логика Силлогизмы
- 98. Регрессивным называется полисиллогизм, в котором заключение просиллогизма становится меньшей посылкой эписиллогизма. Полисиллогизмы Логика Силлогизмы
- 99. Например: надо доказать, что тайное присвоение книги из библиотеки общественно опасно. Для этого построим следующую последовательность
- 100. Полисиллогизмы Логика Силлогизмы
- 101. При помощи прогрессивного полисиллогизма мы поэтапно с максимальной очевидностью перенесли признак «общественно опасный» с общего понятия
- 102. Полисиллогизмы Логика Силлогизмы
- 103. Это – регрессивный полисиллогизм, поскольку заключение просиллогизма «Некоторые преступники способны к самосовершенствованию» является меньшей посылкой эписиллогизма.
- 104. Сокращение простого силлогизма дает энитимему, а сокращение сложного силлогизма – сорит. Полисиллогизмы Логика Силлогизмы
- 105. Полисиллогизмы Сорит – это сложный силлогизм, в котором в каждом из составляющих его простых силлогизмов, начиная
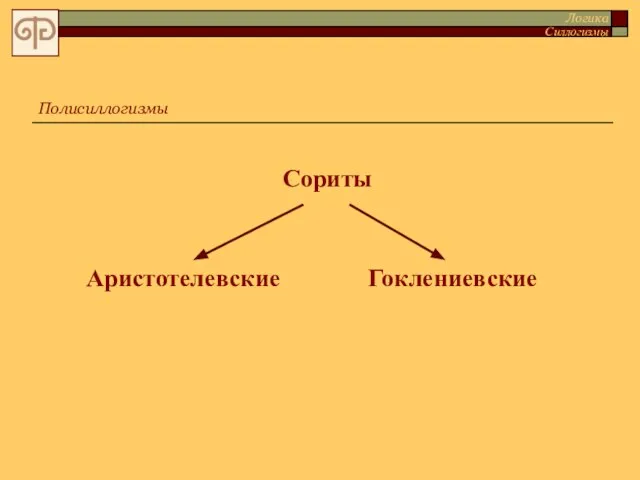
- 106. Полисиллогизмы Логика Силлогизмы Сориты Аристотелевские Гоклениевские
- 107. Полисиллогизмы Сорит, в котором опущена меньшая посылка каждого, начиная со второго, простого силлогизма, называется аристотелевским. Логика
- 108. Полисиллогизмы Сорит, в котором опущена бóльшая посылка каждого, начиная со второго, простого силлогизма, называется гоклениевским. Логика
- 109. Чтобы получить гоклениевский полисиллогизм, просто опустим в наших примерах прогрессивного полисиллогизма бóльшие посылки во всех силлогизмах,
- 110. Полисиллогизмы Логика Силлогизмы
- 111. Аристотелевский сорит будет иметь следующий вид: Полисиллогизмы Логика Силлогизмы
- 112. Развернув аристотелевский сорит в полную форму полисиллогизма, получим следующую последовательность умозаключений: Полисиллогизмы Логика Силлогизмы
- 113. Логика Силлогизмы
- 114. переставить в первом простом силлогизме посылки местами; опустить во всех последующих простых силлогизмах меньшую посылку; опустить
- 115. Полисиллогизмы В аристотелевском сорите происходит доказательство наличия или отсутствия какого-то предиката у известного нам субъекта первой
- 117. Скачать презентацию











































































































 «Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами»
«Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами» Роспись петуха по мотивам Филимоновской росписи
Роспись петуха по мотивам Филимоновской росписи Гражданское право. Понятие и виды сроков в гражданском праве
Гражданское право. Понятие и виды сроков в гражданском праве Модернизм
Модернизм Какие фигуры изображены на рисунке ?
Какие фигуры изображены на рисунке ? Перенос слова переносятся по слогам
Перенос слова переносятся по слогам Принтеры
Принтеры Методическая разработка «Создание презентаций» Элективный курс для 10 класса.
Методическая разработка «Создание презентаций» Элективный курс для 10 класса. Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне
Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне Федеральное Собрание РФ
Федеральное Собрание РФ Инжиниринг нефтехимии и нефтегазопереработки
Инжиниринг нефтехимии и нефтегазопереработки Китайский клуб МИИТа
Китайский клуб МИИТа Мой город, с тебя начинается Родина (город Сатка)
Мой город, с тебя начинается Родина (город Сатка) Спартакиада пенсионеров муниципального образования Город Гатчина
Спартакиада пенсионеров муниципального образования Город Гатчина Эры. Основные события органического мира
Эры. Основные события органического мира Презентация на тему Операционные системы на мобильных устройствах
Презентация на тему Операционные системы на мобильных устройствах  Живопись
Живопись Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы
Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70
Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70 МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942)
МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942) Векторы в пространстве и не только
Векторы в пространстве и не только Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники Трансформация изображения через трансформацию формы - серия открыток
Трансформация изображения через трансформацию формы - серия открыток ОРНАМЕНТЫ в национальном костюме
ОРНАМЕНТЫ в национальном костюме Цветник для солнечного места “Степной бриз ”
Цветник для солнечного места “Степной бриз ” Презентация на тему Тургенев. Стихи в прозе
Презентация на тему Тургенев. Стихи в прозе 287 Воскресшему служу я
287 Воскресшему служу я Берлину заменить Северный поток-2 другим проектом
Берлину заменить Северный поток-2 другим проектом