Содержание
- 2. СОДЕРЖАНИЕ. Задания на соответствие. Математическое лото. Устные задания.
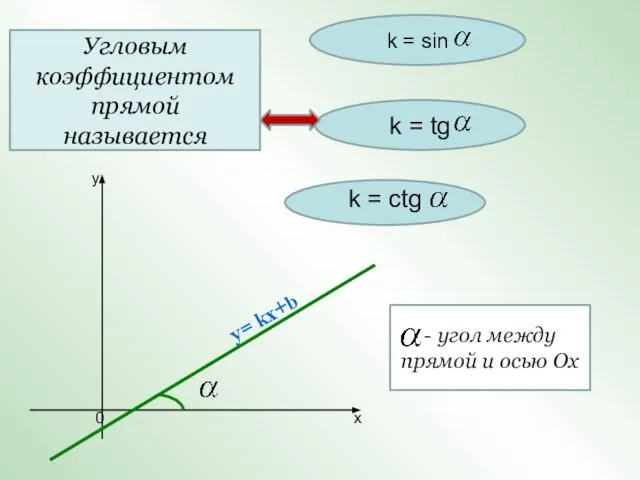
- 3. Угловым коэффициентом прямой называется k = sin k = tg k = ctg - угол между
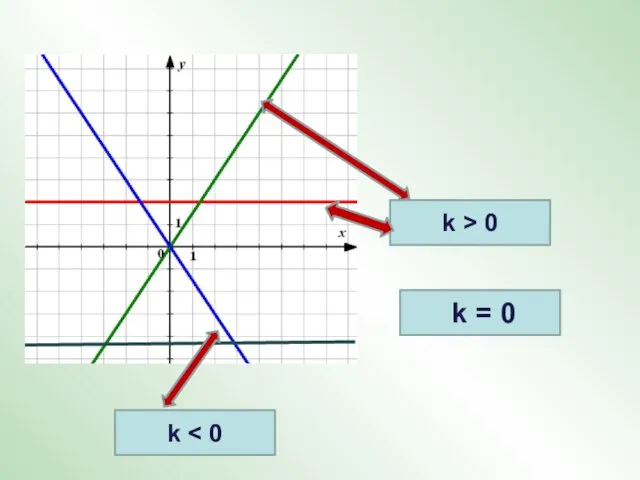
- 4. k = 0 k > 0 k
- 5. Для каждой линейной функции найдите коэффициент k. k = 2 k = 0 k = -1
- 6. Геометрический смысл производной состоит в том, что значение производной функции f(х) в точке х0 равно угловому
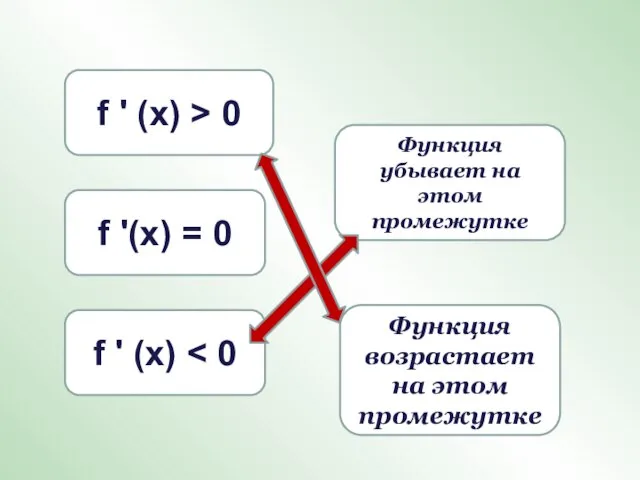
- 7. f ' (х) f ' (х) > 0 Функция убывает на этом промежутке f '(х) =
- 8. Стационарными называют точки, в которых производная функции больше 0 равна 0 больше 1 меньше 0
- 9. Если при переходе через стационарную точку х0 изменяет знак с «–» на «+»; изменяет знак с
- 11. Непрерывная функция у = f(x) задана на отрезке [a; b]. В ответе укажите количество точек графика
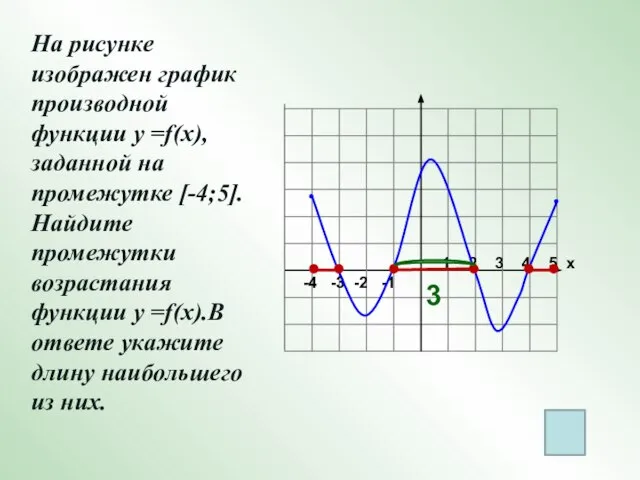
- 12. Непрерывная функция у = f(x) задана на отрезке [a; b]. На рисунке изображен график ее производной
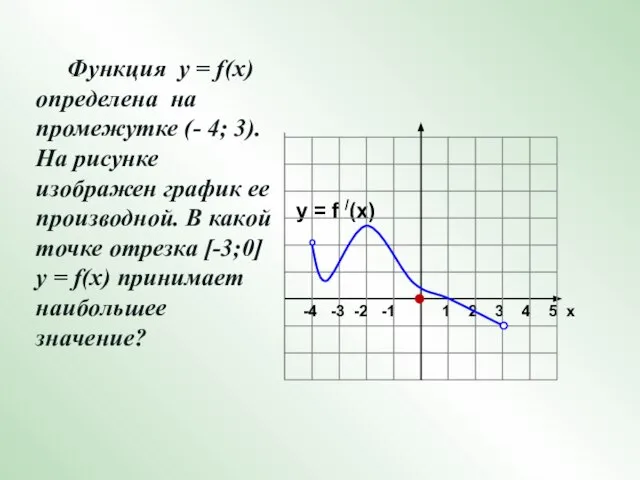
- 13. y = f /(x) 1 2 3 4 5 х -4 -3 -2 -1 Функция у
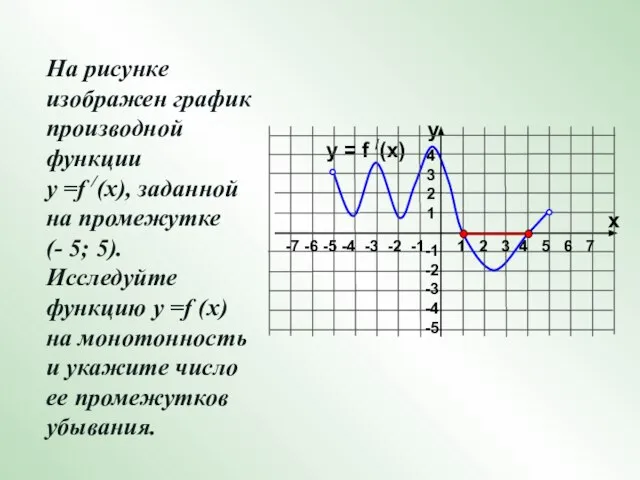
- 14. На рисунке изображен график производной функции у =f /(x), заданной на промежутке (- 5; 5). Исследуйте
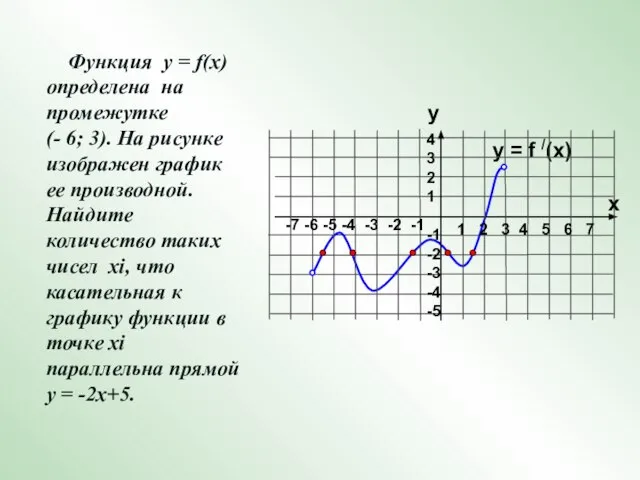
- 15. y = f /(x) Функция у = f(x) определена на промежутке (- 6; 3). На рисунке
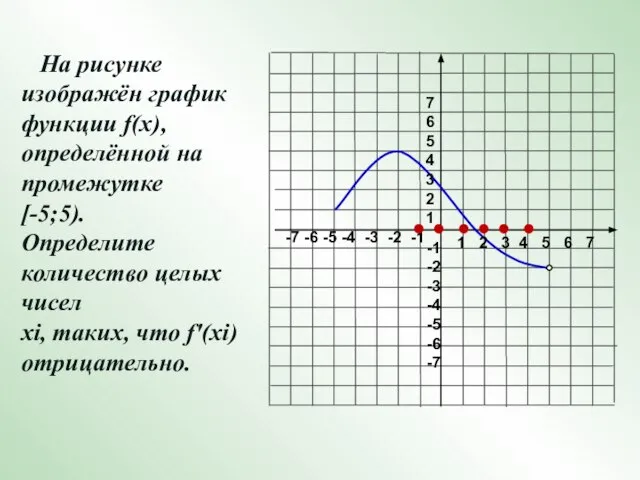
- 16. На рисунке изображён график функции f(x), определённой на промежутке [-5;5). Определите количество целых чисел хi, таких,
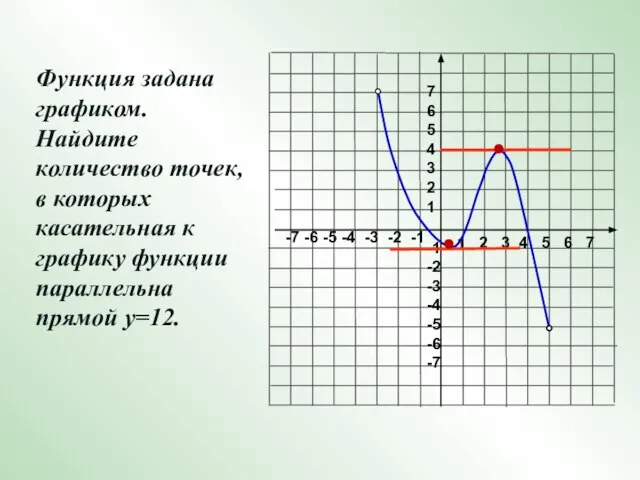
- 17. 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 7 6
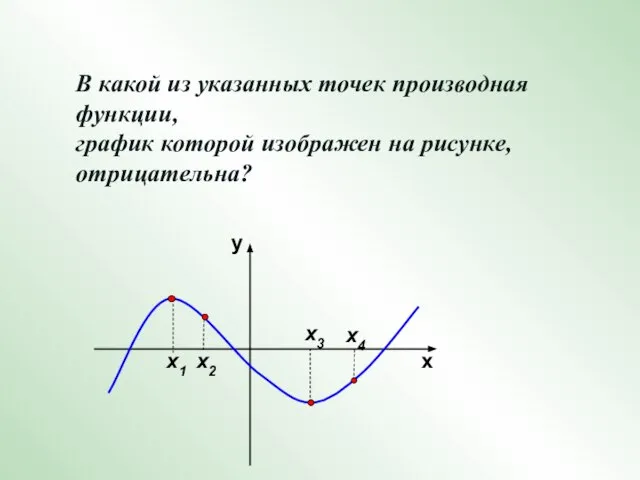
- 18. В какой из указанных точек производная функции, график которой изображен на рисунке, отрицательна? х3 х у
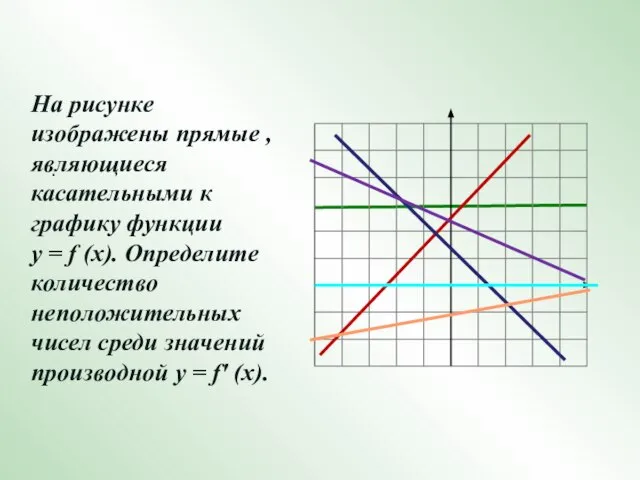
- 19. . На рисунке изображены прямые , являющиеся касательными к графику функции у = f (х). Определите
- 20. Непрерывная функция у = f(x) задана на отрезке [a;b]. На рисунке изображен график её производной. В
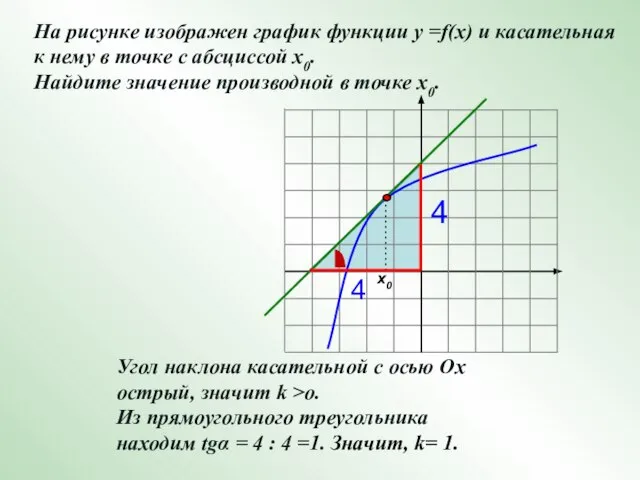
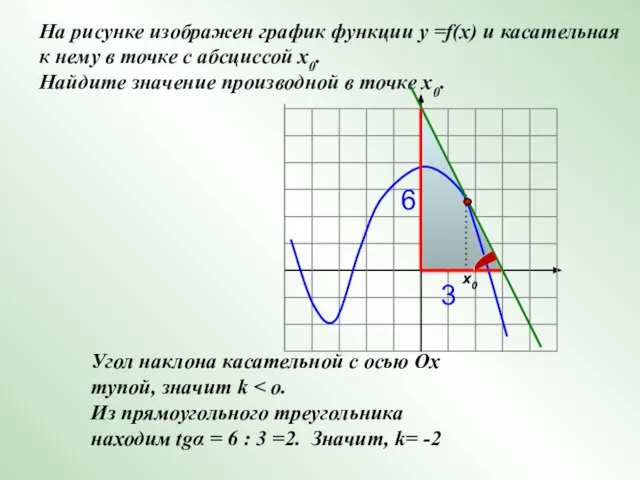
- 21. На рисунке изображен график функции у =f(x) и касательная к нему в точке с абсциссой х0.
- 22. Угол наклона касательной с осью Ох тупой, значит k Из прямоугольного треугольника находим tgα = 6
- 23. -4 -3 -2 -1 1 2 3 4 5 х На рисунке изображен график производной функции
- 25. Скачать презентацию





![Непрерывная функция у = f(x) задана на отрезке [a; b]. В ответе](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/349228/slide-10.jpg)
![Непрерывная функция у = f(x) задана на отрезке [a; b]. На рисунке](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/349228/slide-11.jpg)
![Непрерывная функция у = f(x) задана на отрезке [a;b]. На рисунке изображен](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/349228/slide-19.jpg)
 Шаблон ТюмГУ
Шаблон ТюмГУ Я и мои права
Я и мои права Животноводство
Животноводство Традиции моей семьи (4 класс)
Традиции моей семьи (4 класс) Городецкая роспись
Городецкая роспись Обучение работе с Microsoft Excel
Обучение работе с Microsoft Excel Модернизация процесса геологоразведки
Модернизация процесса геологоразведки Понятие и источники семейного права
Понятие и источники семейного права МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ХИЩНИКИ-ЖЕРТВЫ
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ХИЩНИКИ-ЖЕРТВЫ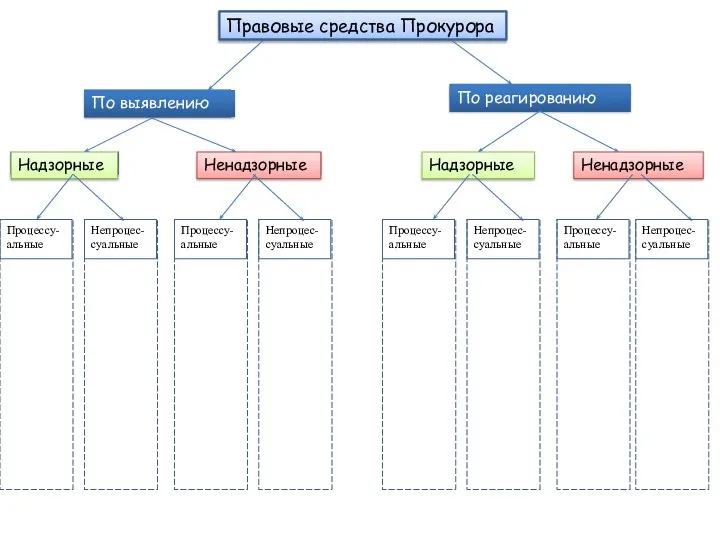 Форма таблицы Правовые средства прокурора
Форма таблицы Правовые средства прокурора Архетипы
Архетипы Системные инновации в многоуровневой подготовке магистров педагогики в области образовательного менеджмента.
Системные инновации в многоуровневой подготовке магистров педагогики в области образовательного менеджмента. Обучение иностранным языкам в современной информационно- образовательной среде
Обучение иностранным языкам в современной информационно- образовательной среде Брошюра Бюджет для граждан
Брошюра Бюджет для граждан Музыка как интонационное выражение христианства
Музыка как интонационное выражение христианства My place
My place Тепловые насосы BROS
Тепловые насосы BROS Презентация Понятие предприним.деят
Презентация Понятие предприним.деят В лес по грибы
В лес по грибы Информация о протекании процессов адаптации в первых классах 2011-2012 уч. год 1 уровень 2 уровень 3 уровень 4 уровень 1А82%13%4%- 1Б79%12,5%8%- 1В52%1
Информация о протекании процессов адаптации в первых классах 2011-2012 уч. год 1 уровень 2 уровень 3 уровень 4 уровень 1А82%13%4%- 1Б79%12,5%8%- 1В52%1 7 способов решения тригонометрического уравнения
7 способов решения тригонометрического уравнения Презентация на тему Возрастные особенности кровеносных сосудов
Презентация на тему Возрастные особенности кровеносных сосудов Промышленный переворот в Англии
Промышленный переворот в Англии  Токарное дело. Хонингование
Токарное дело. Хонингование С пасхой!
С пасхой! Параметризация нелинейных физических процессов в системах мезомасштабного атмосферного моделирования
Параметризация нелинейных физических процессов в системах мезомасштабного атмосферного моделирования Подстраховка и зоны компетенции. По материалам зарубежных публикаций: Flavio Berardi, Andrea Asta
Подстраховка и зоны компетенции. По материалам зарубежных публикаций: Flavio Berardi, Andrea Asta PISA- Programme for Student Assesment – Международная программа по оценке образовательных достижений учащихся
PISA- Programme for Student Assesment – Международная программа по оценке образовательных достижений учащихся