Содержание
- 2. 11-Aug-23 Lecture 9 Uniform Distribution. Normal (Gaussian Distribution) Distributions.
- 3. 11-Aug-23 Contents Uniform distribution – the general view The Normal Distribution
- 4. 11-Aug-23 Uniform Distribution: general view The random variable X is said to have uniform distribution on
- 5. 11-Aug-23 To find the constant C: We use the property of continuous random variable (this property
- 6. 11-Aug-23 So we have in the general terms: For example, if we are interesting in probability
- 7. 11-Aug-23 To find the expectation of the uniformly distributed random variable: We remember the definition of
- 8. 11-Aug-23 To find the expectation of the uniformly distributed random variable: For the uniform distribution
- 9. 11-Aug-23 To find the variance of the uniformly distributed random variable: We remember the definition of
- 10. 11-Aug-23 To find the variance of the uniformly distributed random variable: Substituting the value of and
- 11. 11-Aug-23 To find the variance of the uniformly distributed random variable:
- 12. 11-Aug-23 So the variance of the uniformly distributed random variable: It could be calculated as
- 13. 11-Aug-23 To find the cumulative distribution function for uniform distribution We use the definition of cumulative
- 14. 11-Aug-23 To find the cumulative distribution function for uniform distribution 2. For 3. For
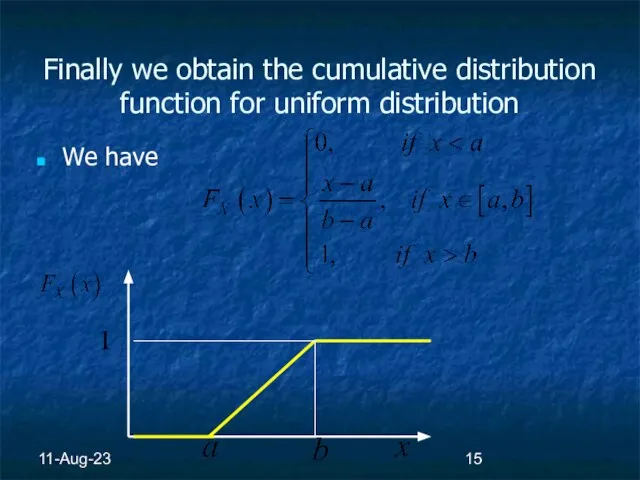
- 15. 11-Aug-23 Finally we obtain the cumulative distribution function for uniform distribution We have
- 16. 11-Aug-23 The Normal Distribution We introduce now a continuous distribution that plays a central role in
- 17. 11-Aug-23 The Normal Distribution If the average score on the test is 60, we would expect
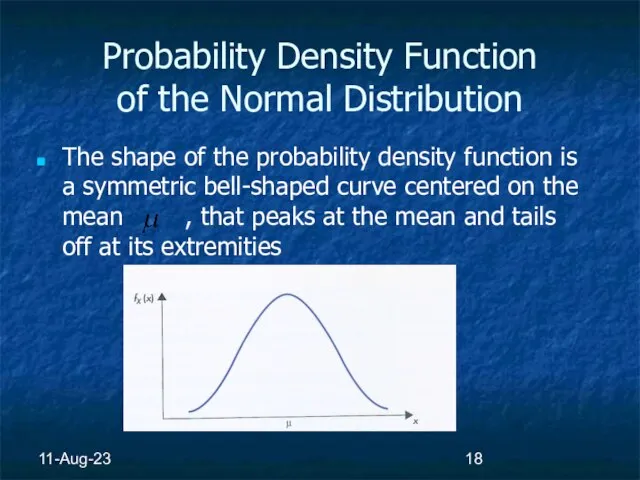
- 18. 11-Aug-23 Probability Density Function of the Normal Distribution The shape of the probability density function is
- 19. 11-Aug-23 Probability Density Function of the Normal Distribution If the random variable X has probability density
- 20. 11-Aug-23 Comments It can be seen from the definition that there is not a single normal
- 21. 11-Aug-23 Some Properties of the Normal Distribution Suppose that the random variable X follows a normal
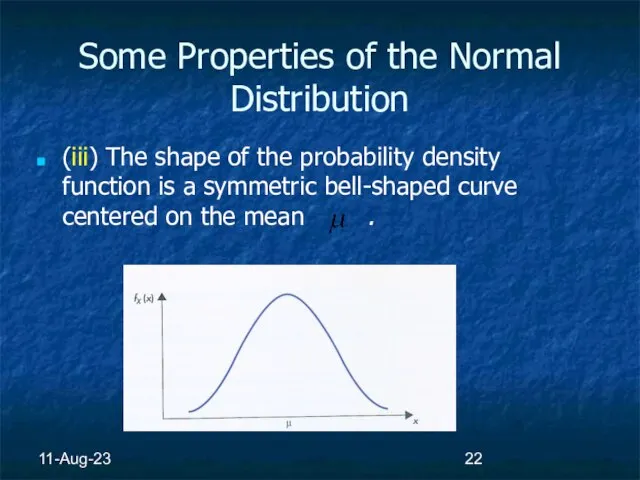
- 22. 11-Aug-23 Some Properties of the Normal Distribution (iii) The shape of the probability density function is
- 23. 11-Aug-23 Comments & Notation It follows from these properties that given the mean and variance of
- 24. 11-Aug-23 Comments Now, the mean of any distribution provides a measure of central location, while the
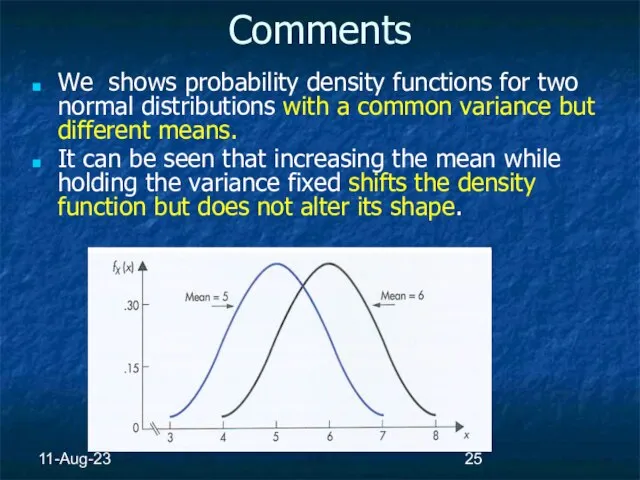
- 25. 11-Aug-23 Comments We shows probability density functions for two normal distributions with a common variance but
- 26. 11-Aug-23 Comments The two density functions are of normal random variables with a common mean but
- 27. 11-Aug-23 Cumulative Distribution Function of the Normal Distribution An extremely important practical question concerns the determination
- 28. 11-Aug-23 Cumulative Distribution Function of the Normal Distribution Suppose that X is a normal random variable
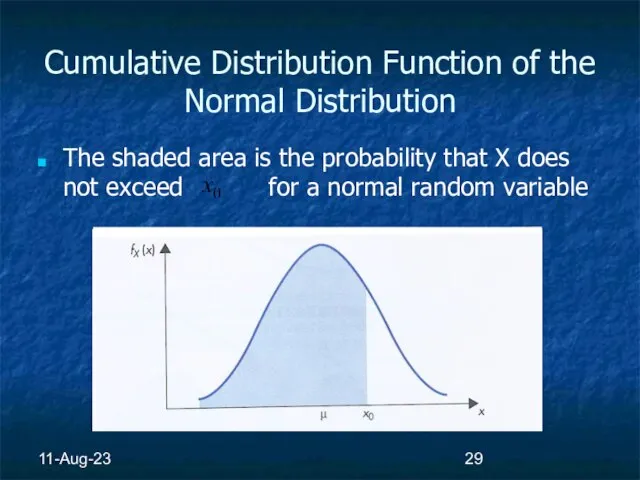
- 29. 11-Aug-23 Cumulative Distribution Function of the Normal Distribution The shaded area is the probability that X
- 30. 11-Aug-23 Cumulative Distribution Function of the Normal Distribution There is no simple algebraic expression for calculating
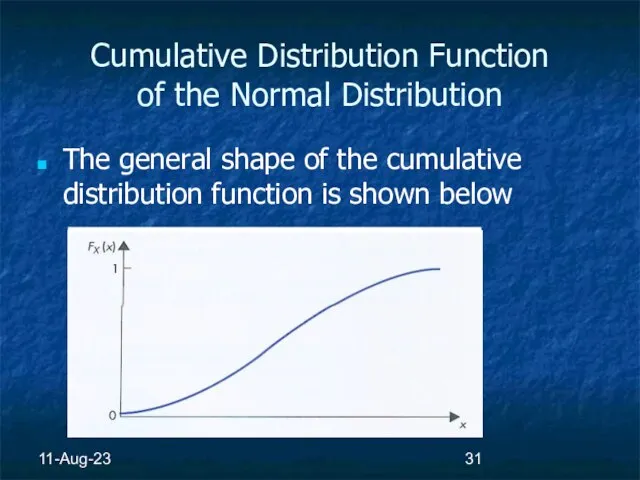
- 31. 11-Aug-23 Cumulative Distribution Function of the Normal Distribution The general shape of the cumulative distribution function
- 32. 11-Aug-23 Range Probabilities for Normal Random Variables We have already seen that for any continuous random
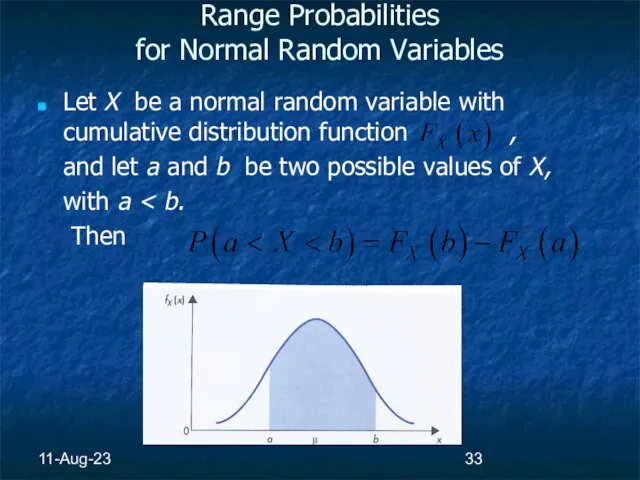
- 33. 11-Aug-23 Range Probabilities for Normal Random Variables Let X be a normal random variable with cumulative
- 34. 11-Aug-23 Range Probabilities for Normal Random Variables Any required probability can be obtained from the cumulative
- 35. 11-Aug-23 Range Probabilities for Normal Random Variables However, it would be enormously tedious if we had
- 36. 11-Aug-23 The Standard Normal Distribution We now introduce the particular distribution that is used for this
- 37. 11-Aug-23 The Standard Normal Distribution If the cumulative distribution function of this random variable is denoted
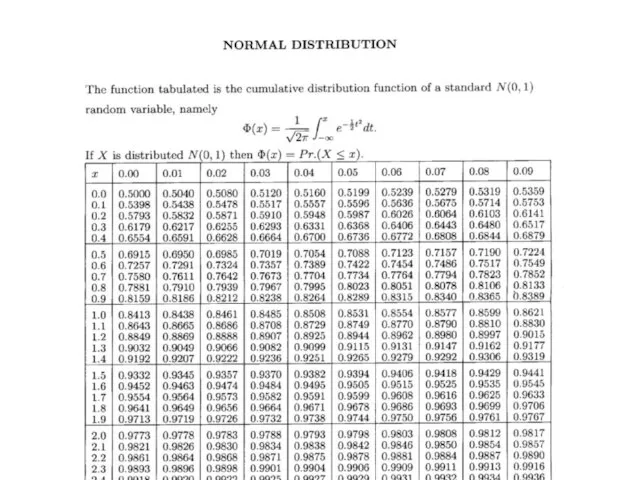
- 38. 11-Aug-23 The table of Normal Distribution This table gives values of for nonnegative values of z.
- 39. 11-Aug-23
- 40. 11-Aug-23 Values of the cumulative distribution function for negative values of z can be inferred from
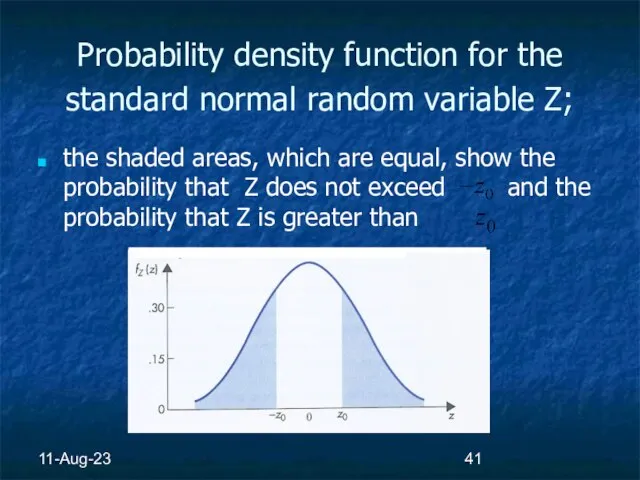
- 41. 11-Aug-23 Probability density function for the standard normal random variable Z; the shaded areas, which are
- 42. 11-Aug-23 Moreover, since the total area under the curve is 1: Hence, it follows that For
- 43. 11-Aug-23 Example If Z is a standard normal random variable, find The required probability is Then,
- 44. 11-Aug-23 How can probabilities for any normal random variable be expressed in terms of those for
- 45. 11-Aug-23 How can probabilities for any normal random variable be expressed in terms of those for
- 46. 11-Aug-23 Finding Range Probabilities for Normal Random Variables Let X be a normal random variable with
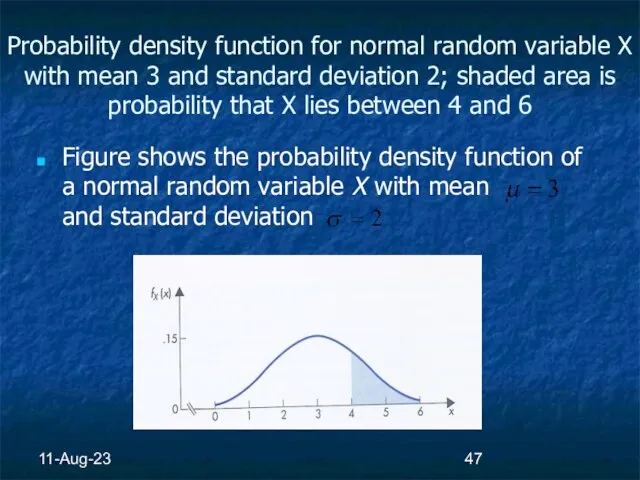
- 47. 11-Aug-23 Probability density function for normal random variable X with mean 3 and standard deviation 2;
- 48. 11-Aug-23 Probability density function for normal random variable X with mean 3 and standard deviation 2;
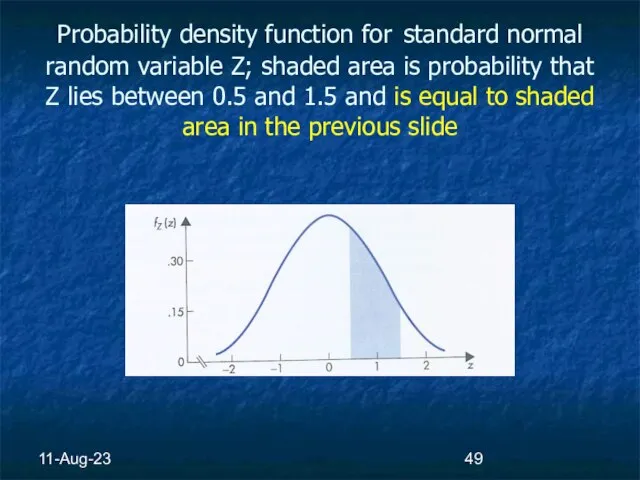
- 49. 11-Aug-23 Probability density function for standard normal random variable Z; shaded area is probability that Z
- 50. 11-Aug-23 Example If X ~ N(15, 16), find the probability that X is larger than 18.
- 51. 11-Aug-23 Example If X is normally distributed with mean 3 and standard deviation 2, find P(4
- 52. 11-Aug-23 Example A company produces lightbulbs whose lifetimes follow a normal distribution with mean 1,200 hours
- 53. 11-Aug-23 Example. Then Hence, the probability is approximately 0.54 that a lightbulb will last between 900
- 54. 11-Aug-23 Example A very large group of students obtains test scores that are normally distributed with
- 55. 11-Aug-23 Example Then we have That is, 3.76% of the students obtained scores in the range
- 56. 11-Aug-23 Example For the test scores of the previous Example, find the cutoff point for the
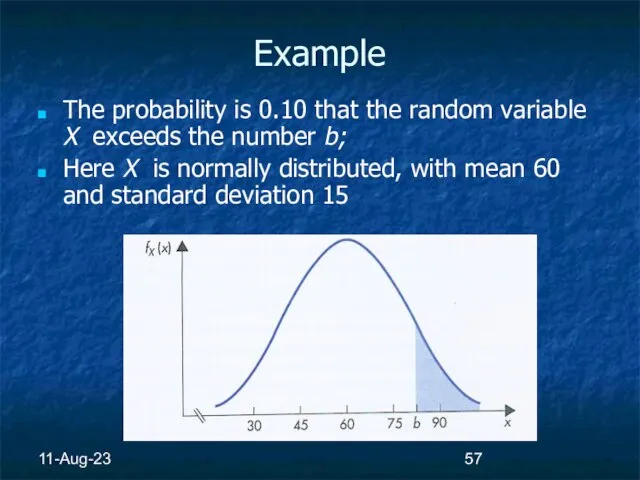
- 57. 11-Aug-23 Example The probability is 0.10 that the random variable X exceeds the number b; Here
- 58. 11-Aug-23 Example Let the number b denote the minimum score needed to be in the highest
- 59. 11-Aug-23 Example So Hence, it follows that Now, from Table, if then z = 1.28.
- 60. 11-Aug-23 Example Therefore, we have So The conclusion is that 10% of the students obtain scores
- 61. 11-Aug-23 Comments In Examples, if the scores awarded on the test were integers, the distribution of
- 63. Скачать презентацию
















































 Формированиеэффективного местного самоуправлениякак задача развития (модернизации) России(вклад г. Киров в стратегию развития
Формированиеэффективного местного самоуправлениякак задача развития (модернизации) России(вклад г. Киров в стратегию развития Культура Западной Европы
Культура Западной Европы Презентация на тему Использование мини-музея в развитии игровой деятельности детей раннего возраста
Презентация на тему Использование мини-музея в развитии игровой деятельности детей раннего возраста История мужской моды и причёсок XVIII — начала XX века
История мужской моды и причёсок XVIII — начала XX века Наследственность в почерке
Наследственность в почерке Анализ деятельности Наркомпроса в контексте его современности
Анализ деятельности Наркомпроса в контексте его современности Кубань - здравница России
Кубань - здравница России Растительная нейробиология
Растительная нейробиология тема ЕДИНАЯ ГОСУДАРСТВЕННАЯ СИСТЕМА ПРЕДУПРЕЖДЕНИЯ И ЛИКВИДАЦИИ ЧРЕЗВЫЧАЙНЫХ СИТУАЦИЙ (РСЧС). Федеральный закон «О защите населе
тема ЕДИНАЯ ГОСУДАРСТВЕННАЯ СИСТЕМА ПРЕДУПРЕЖДЕНИЯ И ЛИКВИДАЦИИ ЧРЕЗВЫЧАЙНЫХ СИТУАЦИЙ (РСЧС). Федеральный закон «О защите населе Нетрадиционные формы урока как средство развития познавательной активности у учащихся на уроках иностранного языка
Нетрадиционные формы урока как средство развития познавательной активности у учащихся на уроках иностранного языка День матери
День матери Философский мистицизм XX века
Философский мистицизм XX века Хлеб
Хлеб Прощай,Азбука!
Прощай,Азбука! Правовой статус несовершеннолетних
Правовой статус несовершеннолетних МОУ Гагаринская СОШРабота с интеллектуально развитыми учащимися
МОУ Гагаринская СОШРабота с интеллектуально развитыми учащимися Инвестиционный проект «Освоение Наталкинского золоторудного месторождения»
Инвестиционный проект «Освоение Наталкинского золоторудного месторождения» Майнкрафт — игра для любителей ставить блоки друг на друга и находить приключения на свою голову
Майнкрафт — игра для любителей ставить блоки друг на друга и находить приключения на свою голову ПРЕЗЕНТАЦИЯ ПО ГЕОМЕТРИИ. НА ТЕМУ: ГЕОМЕТРИЯ В АРХИТЕКТУРЕ
ПРЕЗЕНТАЦИЯ ПО ГЕОМЕТРИИ. НА ТЕМУ: ГЕОМЕТРИЯ В АРХИТЕКТУРЕ Изменения,происходящие с веществами
Изменения,происходящие с веществами Организационно-методическое сопровождение туристско-краеведческой деятельности
Организационно-методическое сопровождение туристско-краеведческой деятельности Sprachgeschichte des Deutschen
Sprachgeschichte des Deutschen Скорость, расстояние, время и таинственные отношения между ними
Скорость, расстояние, время и таинственные отношения между ними Вакуумные моющиеся шины и матрацы для иммобилизации
Вакуумные моющиеся шины и матрацы для иммобилизации Модуль 3
Модуль 3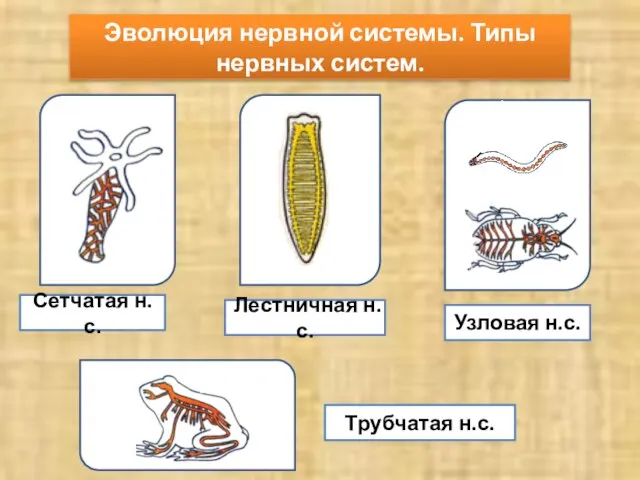 Эволюция нервной системы. Типы нервных систем
Эволюция нервной системы. Типы нервных систем Babilonul (Poarta Zeilor)
Babilonul (Poarta Zeilor) Сплиттеры xDSL
Сплиттеры xDSL