Содержание
- 2. Основные разделы Что такое параллельная программа? Пять стилей параллельного программирования Ноутбук как симметричная мультипроцессорная система (SMP)
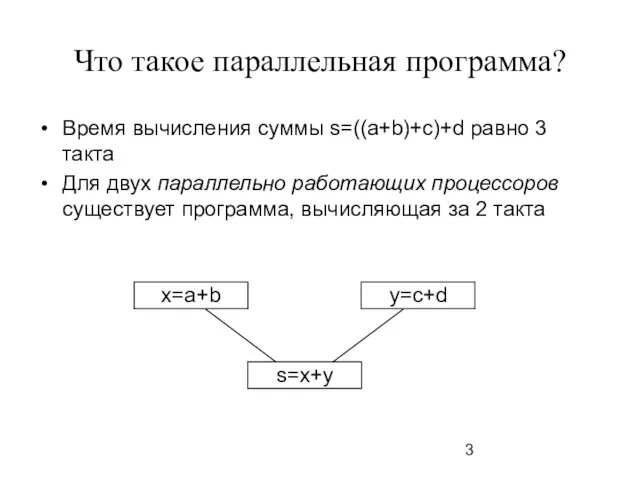
- 3. Что такое параллельная программа? Время вычисления суммы s=((a+b)+c)+d равно 3 такта Для двух параллельно работающих процессоров
- 4. Пять стилей параллельного программирования Итеративный параллелизм Рекурсивный параллелизм Производители и потребители Клиенты и серверы Взаимодействующие каналы
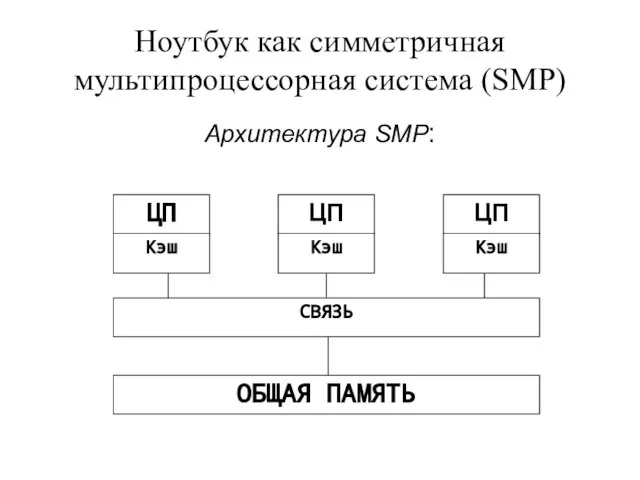
- 5. Ноутбук как симметричная мультипроцессорная система (SMP) Архитектура SMP:
- 6. Как писать параллельные программы? 1. Разрабатываются подпрограммы, которые могут выполняться независимо. Например, для метода трассировки лучей
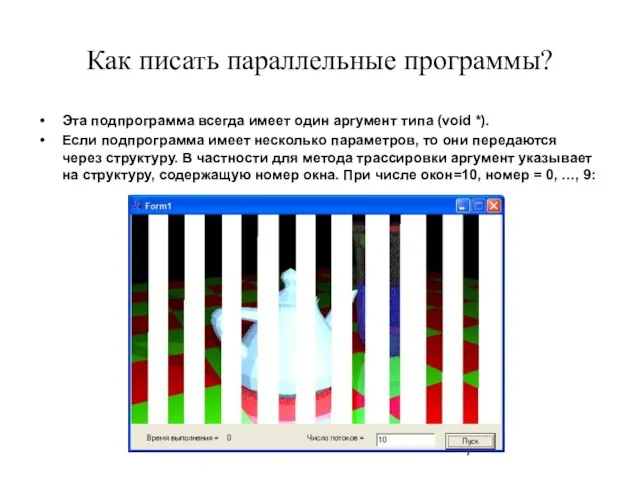
- 7. Как писать параллельные программы? Эта подпрограмма всегда имеет один аргумент типа (void *). Если подпрограмма имеет
- 8. Как писать параллельные программы? Например: struct arg { int ithr ; … }; DWORD WINAPI Part(void
- 9. Итеративный параллелизм и семафоры Метод трассировки лучей реализуется с помощью цикла, в котором на каждом шаге
- 10. Итеративный параллелизм и семафоры
- 11. Итеративный параллелизм и семафоры Для того, чтобы исправить это, введем Определение. Семафором Дейкстры называется структура данных,
- 12. Итеративный параллелизм и семафоры
- 13. Итеративный параллелизм и семафоры Пример программы, в которой решается проблема сериализации. Рассмотрим задачу вычисления интеграла равного
- 14. Итеративный параллелизм и семафоры Напишем главную программу main() { int i; int p[n]; for(i=0; i mut
- 15. Математическое моделирование параллельных вычислительных систем При синхронизации работы потоков с помощью семафоров возникают проблемы, связанные с
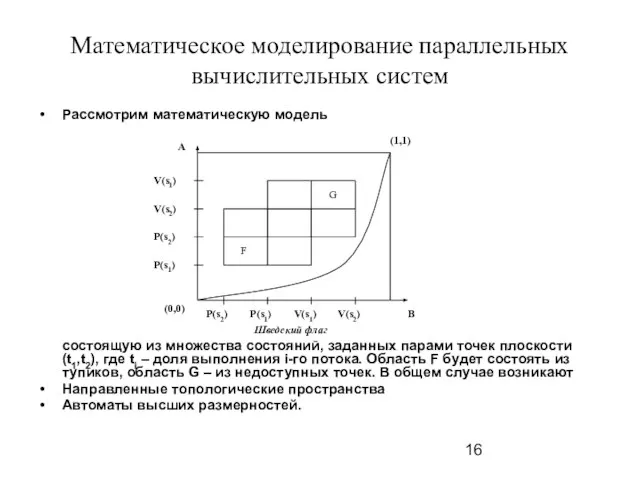
- 16. Математическое моделирование параллельных вычислительных систем Рассмотрим математическую модель состоящую из множества состояний, заданных парами точек плоскости
- 17. Математическое моделирование параллельных вычислительных систем Категория состоит из объектов A,B,C, … и морфизмов , , ,
- 18. Математическое моделирование параллельных вычислительных систем Пусть U: A →B - функтор. Объект A называется универсальным для
- 19. Полукубические множества
- 20. Полукубические множества
- 21. Моноиды трасс и вычислительные процессы Что такое вычислительный процесс? Рассмотрим вычислительную систему, состоящую из операций Определение.
- 22. Моноиды трасс и полукубические множества Теорема 1. Каждому полукубическому множеству с выделенной вершиной соответствует универсальный моноид
- 23. Рекурсивный параллелизм Метод сдваивания int sum(int l, int r) // x[l] + … + x[r] {
- 24. Рекурсивный параллелизм Данные и структура параметров int x[100]; struct arg {int l, r, res}; Вызываемый поток
- 25. Рекурсивный параллелизм Рекурсивный параллелизм применяется для распараллеливания алгоритма перебора с возвратом И.А. Трещев установил в программе
- 26. Конвейерные системы Рассмотрим вычислительную систему для вычисления суммы векторов. Она состоит из 5 микроопераций Comp(a,b) –
- 27. Конвейерные системы Ускорение S5=T1/T5=5nh/((n+4)h) ≈ 5
- 28. Производители и потребители: каналы template class channel { Type *buf; // буфер для очереди int size;
- 29. Производители и потребители: каналы С помощью каналов можно реализовать конвейерные системы. Блок конвейера DWORD WINAPI name_op(void
- 30. Клиент-сервер: задача о читателях и писателях Процессы читают и редактируют файл Имеющие право на чтение –
- 31. Асинхронные системы T=(S,s0,E,I,Tran) S – множество состояний, s0∈ S – начальное состояние, E – множество событий,
- 32. Асинхронные системы a – читатель поступил доступ b – читатель закончил работу с файлом c –
- 33. Асинхронные системы и кубические множества Теорема 2. Каждой асинхронной системе соответствует некоторое кубическое множество. И наоборот,
- 34. Асинхронные системы и кубические множества Асинхронным системам соответствуют также полиэдры – топологические пространства, склеенные из точек,
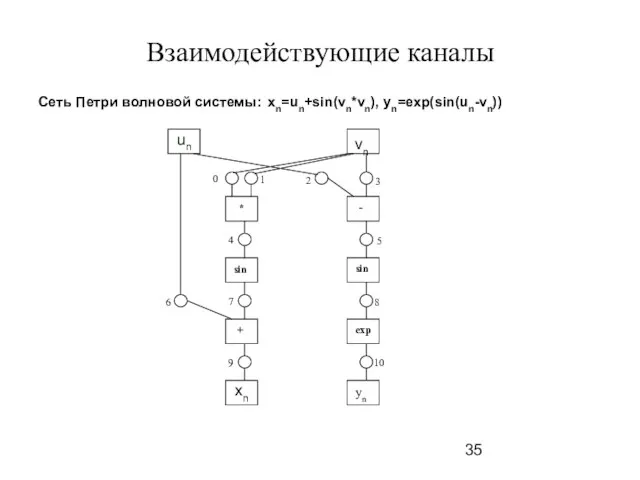
- 35. Взаимодействующие каналы Сеть Петри волновой системы: xn=un+sin(vn*vn), yn=exp(sin(un-vn))
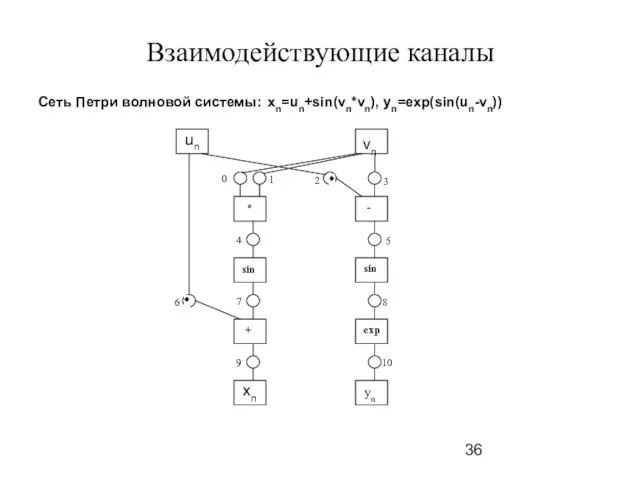
- 36. Взаимодействующие каналы Сеть Петри волновой системы: xn=un+sin(vn*vn), yn=exp(sin(un-vn))
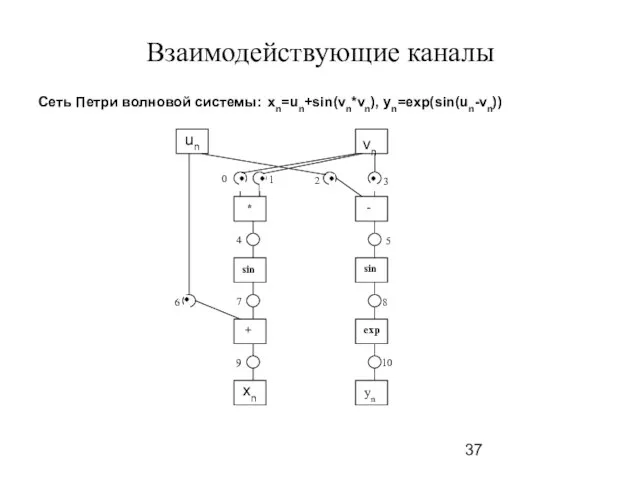
- 37. Взаимодействующие каналы Сеть Петри волновой системы: xn=un+sin(vn*vn), yn=exp(sin(un-vn))
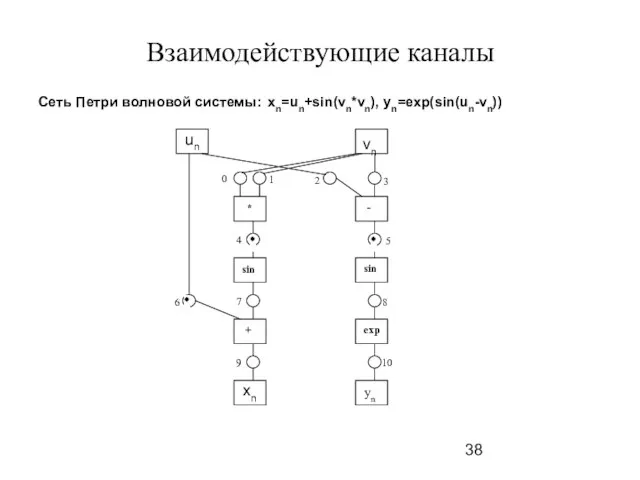
- 38. Взаимодействующие каналы Сеть Петри волновой системы: xn=un+sin(vn*vn), yn=exp(sin(un-vn))
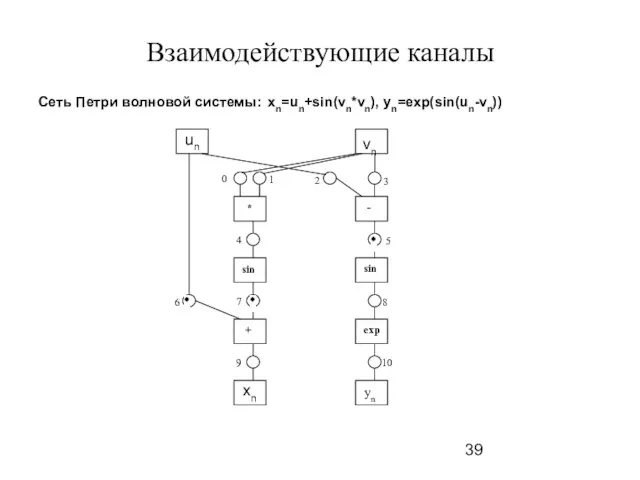
- 39. Взаимодействующие каналы Сеть Петри волновой системы: xn=un+sin(vn*vn), yn=exp(sin(un-vn))
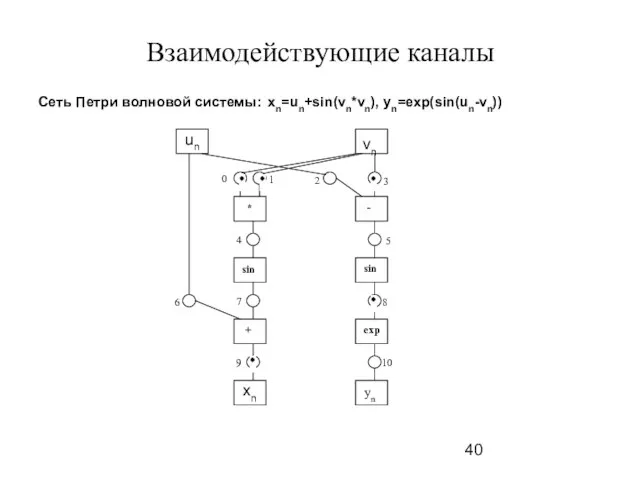
- 40. Взаимодействующие каналы Сеть Петри волновой системы: xn=un+sin(vn*vn), yn=exp(sin(un-vn))
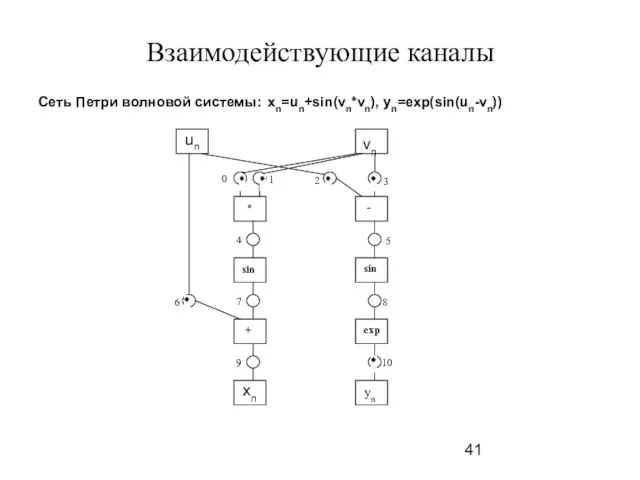
- 41. Взаимодействующие каналы Сеть Петри волновой системы: xn=un+sin(vn*vn), yn=exp(sin(un-vn))
- 42. Взаимодействующие каналы Каналы, соответствующие местам channel *pc[11]; Подпрограмма потока DWORD WINAPI mult(LPVOID) // поток для умножения
- 43. Взаимодействующие каналы Полученные «асинхронные систолические системы» называются волновыми системами Более точная математическая модель волновой системы, чем
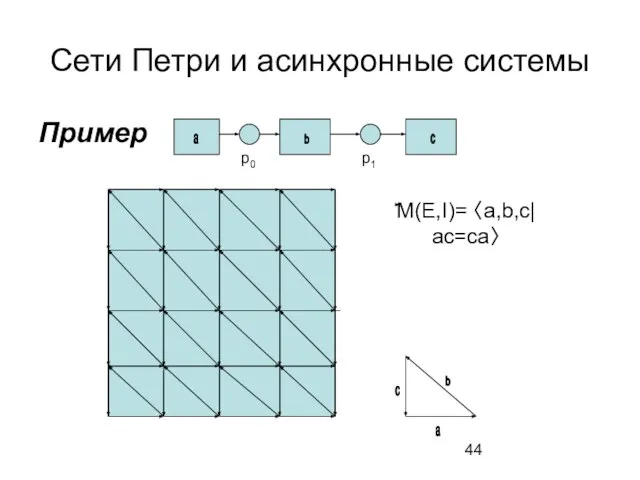
- 44. Сети Петри и асинхронные системы Пример a b c a b c p0 p1 M(E,I)= 〈a,b,c|
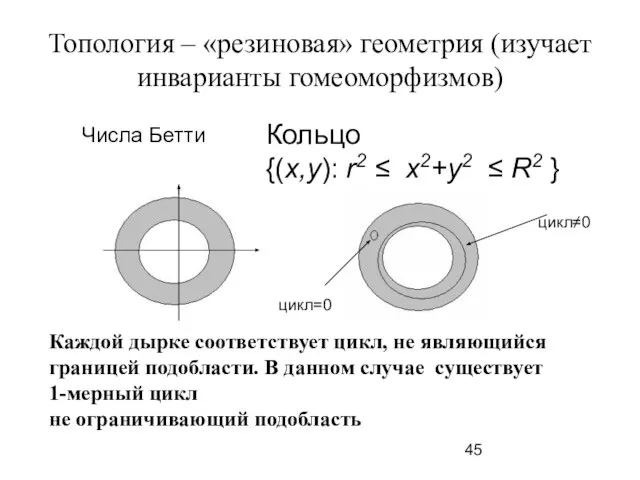
- 45. Топология – «резиновая» геометрия (изучает инварианты гомеоморфизмов) Каждой дырке соответствует цикл, не являющийся границей подобласти. В
- 46. Числа Бетти. Резиновый мяч. Любой 1-мерный цикл является границей поверхности, содержащейся в области {(x,y,z): r2 ≤
- 47. Числа Бетти Сn= L{(x0,x1, …, xn) – симплекс: x0 Zn=dn-1(0), Bn=dn+1Cn+1 Hn=Zn/Bn βn=dim Cn- r(dn)-r(dn+1) Разбиваем
- 48. Числа Бетти . β0=3-0-r(d1)=3-2=1, β1=3-r(d1)-0=1 2-цепей нет ⇒ цикл 01+12-02 ≠ 0
- 49. Вычисление чисел Бетти βn= dim Cn – r( dn )– r (dn+1) С0 = L{0,1,2,3} ≈
- 50. Числа Бетти полукубических множеств d1= d2=
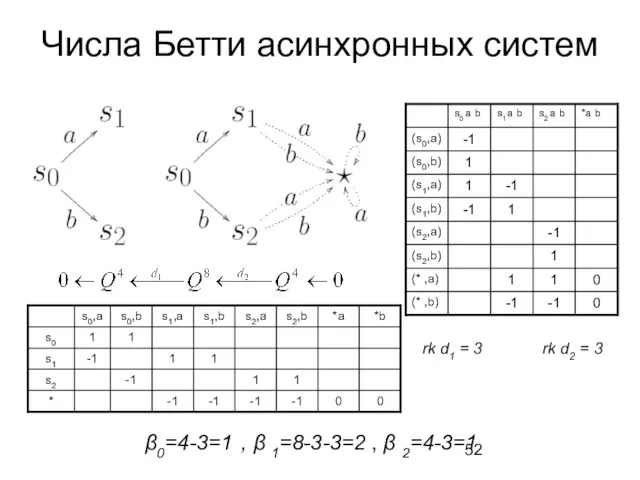
- 51. Числа Бетти асинхронных систем S0=S∪{*}, S1={(s,e1): s∈S0,e1 ∈E}, … , Sn= {(s, e1 , …, en):
- 52. Числа Бетти асинхронных систем rk d1 = 3 β0=4-3=1 , β 1=8-3-3=2 , β 2=4-3=1 rk
- 53. Числа Бетти асинхронных систем 28 октября (четверг), в 12.00, в 201/3 состоится защита диссертации В.Е. Лопаткина
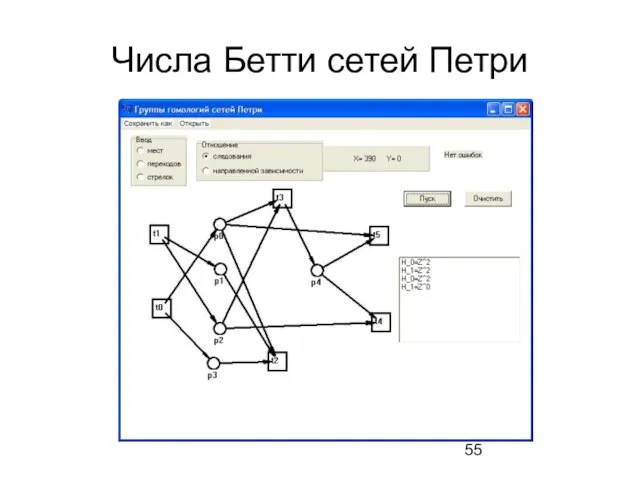
- 54. Числа Бетти сетей Петри 2 подхода к определению чисел Бетти сетей Петри: Сети Петри сопоставляется асинхронная
- 55. Числа Бетти сетей Петри
- 57. Скачать презентацию

















![Рекурсивный параллелизм Метод сдваивания int sum(int l, int r) // x[l] +](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/411992/slide-22.jpg)
![Рекурсивный параллелизм Данные и структура параметров int x[100]; struct arg {int l,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/411992/slide-23.jpg)










![Взаимодействующие каналы Каналы, соответствующие местам channel *pc[11]; Подпрограмма потока DWORD WINAPI mult(LPVOID)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/411992/slide-41.jpg)









 Владимир Владимир Маяковский
Владимир Владимир Маяковский  Кукольный спектакль Зайкина тётя
Кукольный спектакль Зайкина тётя Презентация на тему Язык HTML
Презентация на тему Язык HTML Культура во второй половине XX-начале XXI века.
Культура во второй половине XX-начале XXI века. Сделай свое лето со 2 июня по 3 августа 2019 года включительно (период действия каталогов №№8–10 2019 года)
Сделай свое лето со 2 июня по 3 августа 2019 года включительно (период действия каталогов №№8–10 2019 года) Презентация на тему: Информация, как основная сущность теории информации
Презентация на тему: Информация, как основная сущность теории информации Тип губки
Тип губки использование религиозных символов в коммерческой рекламе
использование религиозных символов в коммерческой рекламе Prezentatsia1
Prezentatsia1 A real professional. What does it mean?
A real professional. What does it mean? Santa Claus
Santa Claus Внутренняя политика России в начале XXI века – восстановление государства
Внутренняя политика России в начале XXI века – восстановление государства Общественная жизнь России при Николае I
Общественная жизнь России при Николае I Le frasi ridicole
Le frasi ridicole Предложения по подготовке специалистовдля реализации проектов по коммерциализации товаров и услуг ГНСС «ГЛОНАСС»
Предложения по подготовке специалистовдля реализации проектов по коммерциализации товаров и услуг ГНСС «ГЛОНАСС» Создание культурной среды при обучении младших школьников иностранному языку
Создание культурной среды при обучении младших школьников иностранному языку Технические кодексы установившейся практики в области охраны окружающей среды и природопользования
Технические кодексы установившейся практики в области охраны окружающей среды и природопользования Одуванчик
Одуванчик Введение в теорию производства
Введение в теорию производства "ПО ДОРОГАМ ГРАЖДАНСКОЙ ВОЙНЫ"
"ПО ДОРОГАМ ГРАЖДАНСКОЙ ВОЙНЫ" Как фотографировать высокое сооружение
Как фотографировать высокое сооружение Презентация на тему Роль права в жизни государства
Презентация на тему Роль права в жизни государства Презентация на тему Деревья леса
Презентация на тему Деревья леса l_sapr_1-7
l_sapr_1-7 Эффективные способы использования заемных средств, способствующие развитию бизнеса.
Эффективные способы использования заемных средств, способствующие развитию бизнеса. Алиса в стране чудес
Алиса в стране чудес Добровольцы мы (3 раза) В армии Христа. Смело мы идем за своим Вождем, С Ним мы победим врага.
Добровольцы мы (3 раза) В армии Христа. Смело мы идем за своим Вождем, С Ним мы победим врага. Особенности проведенияЕГЭв штатном режиме
Особенности проведенияЕГЭв штатном режиме