Содержание
- 2. 4. Векторным произведением двух векторов a и b называется ВЕКТОР с= [ a, b ] такой,
- 3. 5. Смешанным произведением трех векторов a , b и с называется ЧИСЛО 5.а Геометрический смысл модуля
- 4. Уравнение прямой, проходящей через две данные точки Уравнение прямой с угловым коэффициентом Уравнение прямой, проходящей через
- 5. Угол между прямыми на плоскости Условие параллельности прямых Условие перпендикулярности прямых
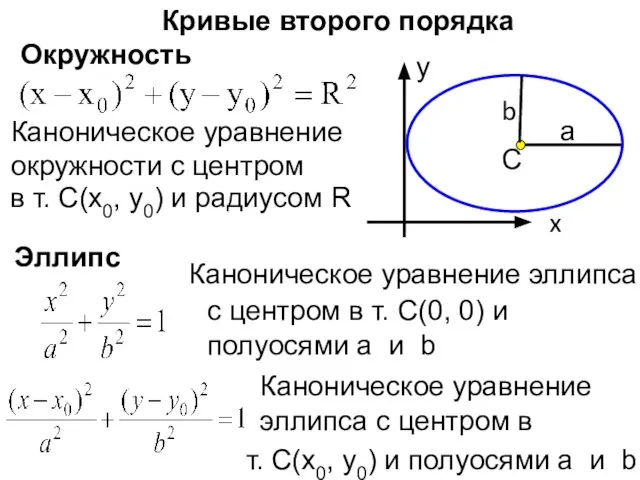
- 6. Кривые второго порядка Окружность x у С а Каноническое уравнение окружности c центром в т. С(х0,
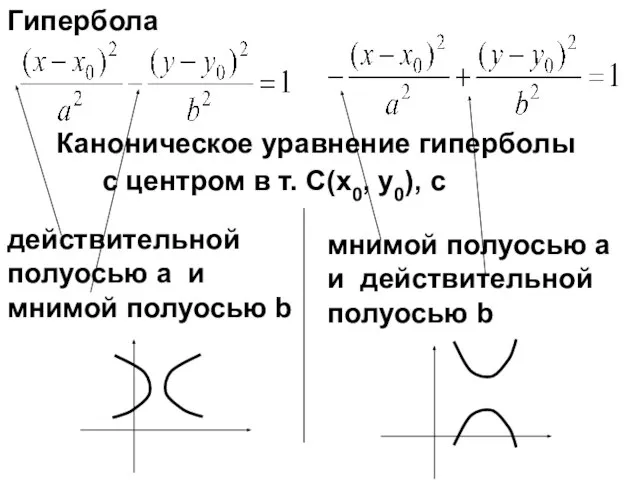
- 7. Каноническое уравнение гиперболы действительной полуосью a и мнимой полуосью b мнимой полуосью a и действительной полуосью
- 8. Каноническое уравнение параболы c вершиной в т. С(х0, у0), с с осью симметрии параллельной ОХ ОУ
- 9. Правила дифференцирования Производная сложной функции f ′ (x)=f ′(φ(ψ(μ(x))))⋅φ′(ψ(μ(x)))⋅ψ′(μ(x))⋅μ′(x) у=f(φ(ψ(μ(x))))
- 10. Таблица производных x′ = 1 (xn)′ = nxn-1 (sinx)′ = сos x (cosx)′ = -sin x
- 12. Свойства неопределенного интеграла
- 13. Дифференциал функции Формула интегрирования по частям КРУГОВОЙ
- 14. Формула Ньютона-Лейбница Площадь плоской фигуры Длина кривой Объем тела, образованного вращением криволинейной трапеции вокруг оси ОХ
- 15. Дифференциальные уравнения первого порядка 1. С разделенными переменными М(х) dx + S(y)dy=0 2. С разделяющимися переменными
- 16. Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами у= z(x) и y= g(x) частные решения
- 17. Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами Сумма у=yоо +учн - общее решение уравнения,
- 18. О.1. Бесконечная сумма элементов называется числовым рядом, общий член ряда последовательности вида О.3. - ряд сходится,
- 19. Достаточные признаки сходимости числовых рядов 1. Интегральный признак Коши сходится расходится сходится расходится сходится расходится Ряд
- 21. Скачать презентацию







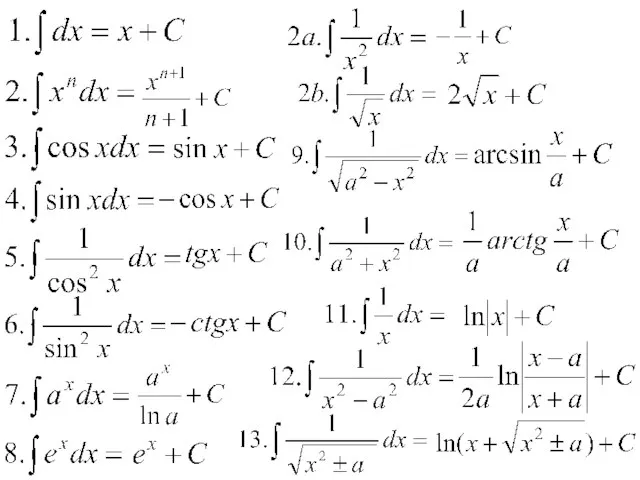








 Технология монолитного бетона и железобетона. (Лекция 8)
Технология монолитного бетона и железобетона. (Лекция 8) Механическое движение Тест 2
Механическое движение Тест 2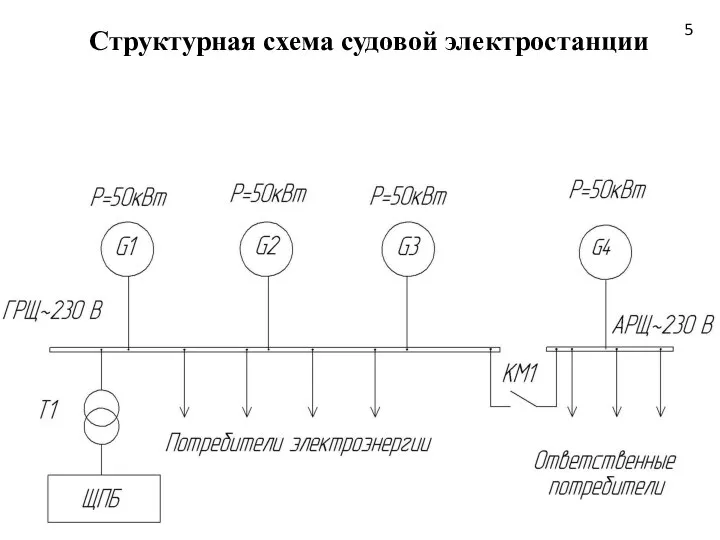 Структурная схема судовой электростанции
Структурная схема судовой электростанции Антон Павлович Чехов
Антон Павлович Чехов Скрипты действий ЦОМП при закрытии участков. Служба пассажирских сервисов
Скрипты действий ЦОМП при закрытии участков. Служба пассажирских сервисов Десант из детсада
Десант из детсада Презентация на тему Северная Америка
Презентация на тему Северная Америка РАССЛЕДОВАНИЕ ДОВЕДЕНИЙ ДО САМОУБИЙСТВА
РАССЛЕДОВАНИЕ ДОВЕДЕНИЙ ДО САМОУБИЙСТВА Человек и человечность. Что такое гуманизм
Человек и человечность. Что такое гуманизм Презентация по английскому Местоимения some any no
Презентация по английскому Местоимения some any no Презентация на тему графическое решение квадратных уравнений 8 класс
Презентация на тему графическое решение квадратных уравнений 8 класс  Методы и приборы разрушающего контроля, применяемые при обследовании
Методы и приборы разрушающего контроля, применяемые при обследовании Суть и содержание управления проектами
Суть и содержание управления проектами Гималаи
Гималаи Умножение и деление и десятичных дробей на натуральные числа Ульянова Антонина Николаевна, МБОУ» Малобуяновская ООШ» 2012.
Умножение и деление и десятичных дробей на натуральные числа Ульянова Антонина Николаевна, МБОУ» Малобуяновская ООШ» 2012. Схемы оплаты перевозок по пластиковым (банковским) картам при электронном билетооформлении
Схемы оплаты перевозок по пластиковым (банковским) картам при электронном билетооформлении Соціальні медіа для бібліотек Конференція Крим-2011, м. Судак. - презентация
Соціальні медіа для бібліотек Конференція Крим-2011, м. Судак. - презентация Образец оформления конспекта
Образец оформления конспекта МБОУ «Староайбесинская СОШ» презентация10 класса
МБОУ «Староайбесинская СОШ» презентация10 класса Свободное падение
Свободное падение Средства массовой информации и анализ информационных программ
Средства массовой информации и анализ информационных программ Краеваяобразовательная программа «Солнечное озеро»в рамках Краевой программы «Поколение XXI: развитие человеческого потенциала
Краеваяобразовательная программа «Солнечное озеро»в рамках Краевой программы «Поколение XXI: развитие человеческого потенциала Математика
Математика Индикаторы мониторинга прогресса в осуществлении целей Стратегии экологических партнерств для стран ВЕКЦА
Индикаторы мониторинга прогресса в осуществлении целей Стратегии экологических партнерств для стран ВЕКЦА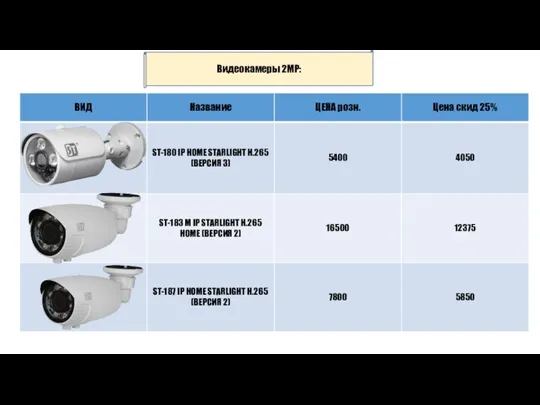 Видеокамеры 2MP
Видеокамеры 2MP Неразветвленные RLC цепи
Неразветвленные RLC цепи تجار سازی محصول - کد 20318
تجار سازی محصول - کد 20318 Симметрия вокруг нас
Симметрия вокруг нас