Решение неравенств первой степени с одной переменной

Тема: решение неравенств первой степени с одной
переменной (графический способ решения) ах + в > o cх + d < в
ах + в ≤ cх + d

Цели урока:
Повторить свойства числовых неравенств, научиться решать эти неравенства графическим способом, закрепить полученные знания на практической работе;
развитие математи-ческого кругозора, логического мышления, культуры речи;
воспитание интереса к математике.
Оборудование:
Планшетки с координатной плоскостью;
фломастеры, мелки разных цветов, линейки;
компьютеры.

Устный счет – зарядка для ума.
На основании каких свойств числовых неравенств можно утверждать:
если х > у, то 15х > 15у
-9х < -9у
х + 20 > у + 20
х > у
3 3
Известно, что а > в. Верно ли, что а + 5 > в + 4,
а + 3 > в + 6
а > в, что можно сказать о разности а – в,
Сравнить а и в, если разность в - а < 0

Актуализация знаний
Решить данные неравенства (с объяснением свойств, используемых при решении), на числовой прямой указать решение и записать ответ числовым промежутком:
а) 2х + 6 > 0,
в) х + 4 < 6,
с) 4х – 7 > х - 4.
Этапы графического решения уравнений.
Построение графиков линейных функций вида:
а) у = 0; в) у = с; с) у = kх + b; d) y =kx + d у
у = kx+b
у = с
b
х
у = 0
d
y = kx+d

Исследовательская групповая работа
В одной системе координат (на планшетах с координатной плоскостью) построить графики функций:
а) у = 2х + 6 и у = 0 и решить неравенство: 2х + 6 > 0
у
у = 2 х + 6
6
у = 0
-6 -3 0 3 6 х

в) построить графики у = х + 4 и у = 6 и решить неравенство: х + 4 < 6
у
6
у = 6
4
у = х+4
-6 -4 -2 0 2 4 6 х

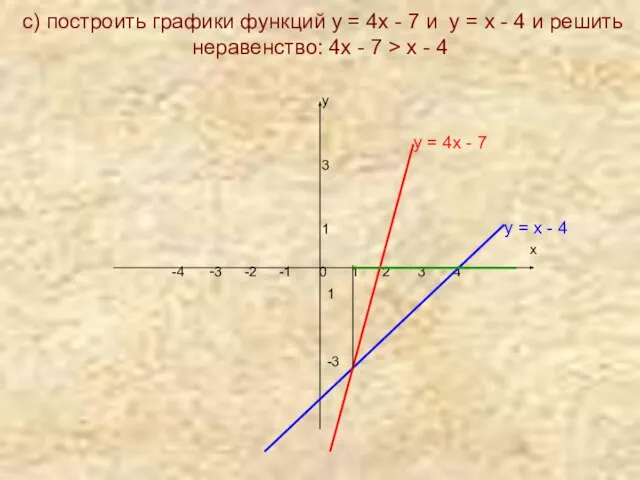
с) построить графики функций у = 4х - 7 и у = х - 4 и решить неравенство: 4х - 7 > х - 4
у
у = 4х - 7
3
1 у = х - 4
х
-4 -3 -2 -1 0 1 2 3 4
1
-3

d) решить графически неравенства: х + 2 < х + 5 х - 3 > х + 2
у
у=х+5
у = х + 2
5
4
3
2
1
-5 -4 -3 -2 -1 0 1 2 3 4 5 х
-1
-2
-3
-4
-5
у = х- 3

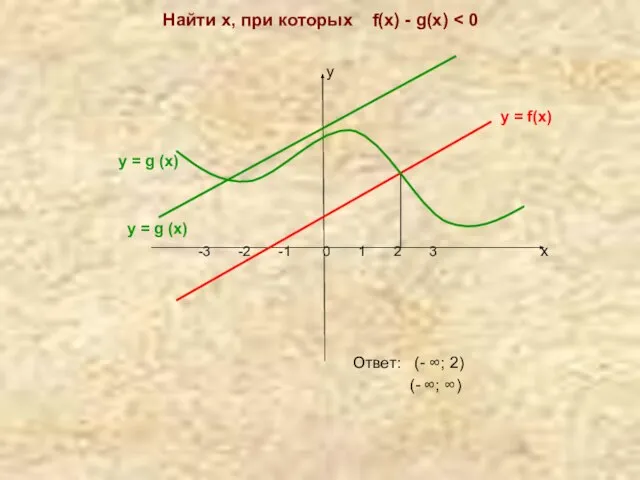
Работа учащихся на компьютерах
Найти х, при которых f(х) < g(х),
f(х) - g(х)> 0
у
у = f(х)
у = g(х)
-3 -2 -1 0 1 2 3 х
у = f(х)
Ответ: (- ∞; 1)
решения нет

Найти х, при которых f(х) - g(х) < 0
у
у = f(х)
у = g (х)
у = g (х)
-3 -2 -1 0 1 2 3 х
Ответ: (- ∞; 2)
(- ∞; ∞)

Итог урока
Повторили:
свойства числовых неравенств, этапы решения неравенств первой степени,
способы записи решений этих неравенств, построение графиков линейных функций;
Научились решать неравенства первой степени графическим способом;
Пробовали применять на практике полученные на уроке знания.