Содержание
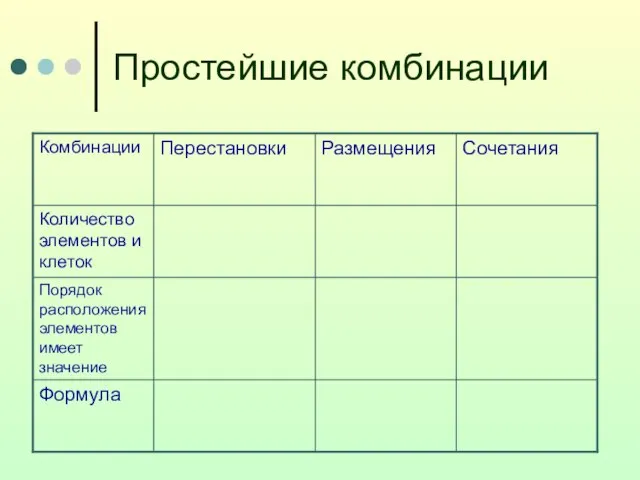
- 2. Простейшие комбинации
- 3. Простейшие комбинации
- 4. Правило умножения! Если элемент А можно выбрать m способами, а элемент В можно выбрать n способами,
- 5. Устный счет Вычислить:
- 6. Вычислите:
- 7. 9.57 В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для
- 8. 9.58 В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать
- 9. 9.62 В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить четырех мальчиков
- 10. Задача 1 Сколькими способами могут разместиться 4 пассажира в 4-хместной каюте? 24 4 16
- 11. Задача 2. Четыре человека обменялись рукопожатиями. Сколько было всего рукопожатий? 4 6 8
- 12. Задача 3. Сколько бригад по 3 человек в каждой можно составить из 7 человек для отправки
- 13. Задача 4. Определить число диагоналей 5-тиугольника. 10 5 20
- 14. Задача 5. Сколькими способами могут быть распределены золотая и серебряная медали по итогам олимпиады, если число
- 15. Задача 6. В школьной столовой на обед приготовили в качестве вторых блюд мясо, котлеты и рыбу.
- 16. Задача 7. Трое господ при входе в ресторан отдали швейцару свои шляпы, а при выходе получили
- 17. Решение задач из сборника. 9.64 (а) (б) 9.66 (а) (б) (в) 9.69
- 18. Проверочная работа 1 вариант 1. Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации.
- 19. Молодец!!!
- 20. Подумай ещё!!!
- 21. Ответы 1 вариант 2 вариант
- 23. Скачать презентацию



















 Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной
Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной Средства регулирования движением поездов
Средства регулирования движением поездов Афины при Перикле
Афины при Перикле Электронная таблица EXCEL
Электронная таблица EXCEL Архетипы
Архетипы УНИДРУА: международный институт по унификации частного права
УНИДРУА: международный институт по унификации частного права Органы чувств
Органы чувств  «Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения»
«Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения» Новогодние открытки
Новогодние открытки Робототехника. Проект
Робототехника. Проект Балансирующий рынок
Балансирующий рынок Теорема Пифагора
Теорема Пифагора Культура XX века
Культура XX века Деревня Юрьевец
Деревня Юрьевец Wine. The benefits of wine with moderate consumption
Wine. The benefits of wine with moderate consumption Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов
Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов Воздействие высокоскоростных магистралей на окружающую среду
Воздействие высокоскоростных магистралей на окружающую среду Презентация экскурсии в животноводческий комплекс «ИП Каюмов»
Презентация экскурсии в животноводческий комплекс «ИП Каюмов» 07_0___163
07_0___163 каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в
каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в «Белые» в Гражданской войне
«Белые» в Гражданской войне Внедрение здоровьесберегающих технологий
Внедрение здоровьесберегающих технологий Русское искусство 2 пол.19 века
Русское искусство 2 пол.19 века Всегда ли правы мы- родители?
Всегда ли правы мы- родители? Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова
Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова Семейные традиции семьи Митрофановых
Семейные традиции семьи Митрофановых HADI – это экспериментальный научный метод исследования, переложенный на бизнес
HADI – это экспериментальный научный метод исследования, переложенный на бизнес ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс
ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс