С2 ЕГЭ

Угол между прямыми.

направляющие
вектора прямых
а
b

№ 1. В правильной шестиугольной призме все ребра равны 1. Найдите косинус угла между прямыми АВ1 и ВF1
F1 (- 1; 0;1)

направляющие
вектора прямых
Ответ:

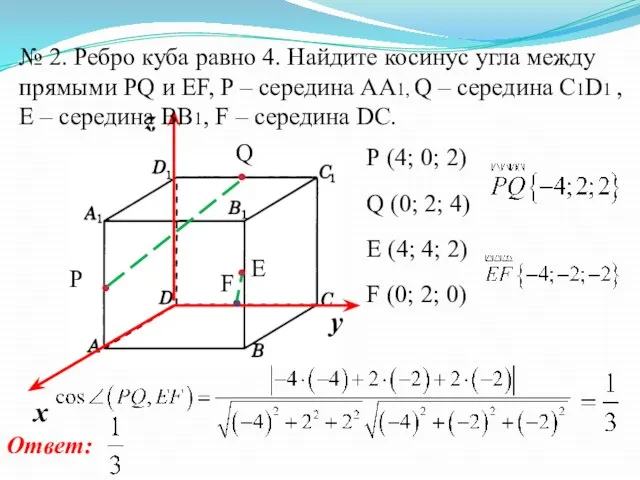
№ 2. Ребро куба равно 4. Найдите косинус угла между прямыми PQ и EF, P – середина АА1, Q – середина С1D1 , Е – середина ВВ1, F – середина DC.
P
Q
E
F
Р (4; 0; 2)
Q (0; 2; 4)
E (4; 4; 2)
F (0; 2; 0)
Ответ:

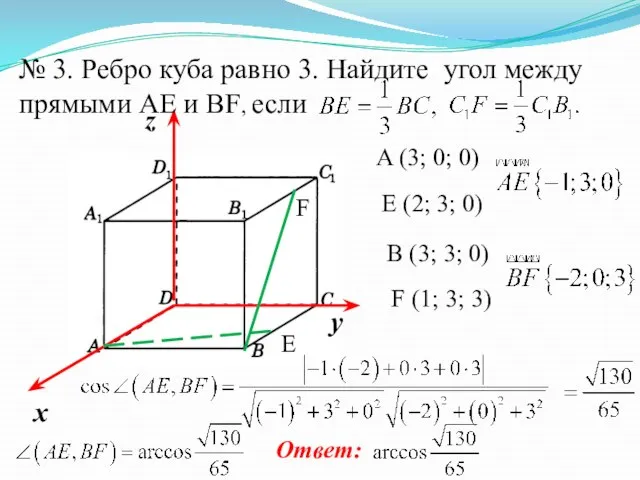
E
F
№ 3. Ребро куба равно 3. Найдите угол между прямыми AE и BF, если
A (3; 0; 0)
Е (2; 3; 0)
В (3; 3; 0)
F (1; 3; 3)
Ответ:

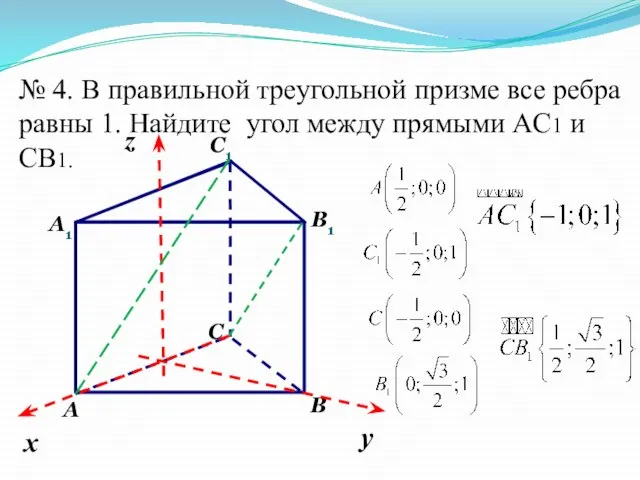
№ 4. В правильной треугольной призме все ребра равны 1. Найдите угол между прямыми AС1 и СB1.

Ответ:

Угол между прямой и плоскостью.

α
β
α - угол между прямой и плоскостью
β – угол между прямой и перпендикуляром
к плоскости
Чтобы найти синус угла между прямой
и плоскостью можно найти косинус угла между прямой и перпендикуляром к плоскости
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.

уравнение плоскости
- вектор нормали к плоскости
- направляющий вектор прямой

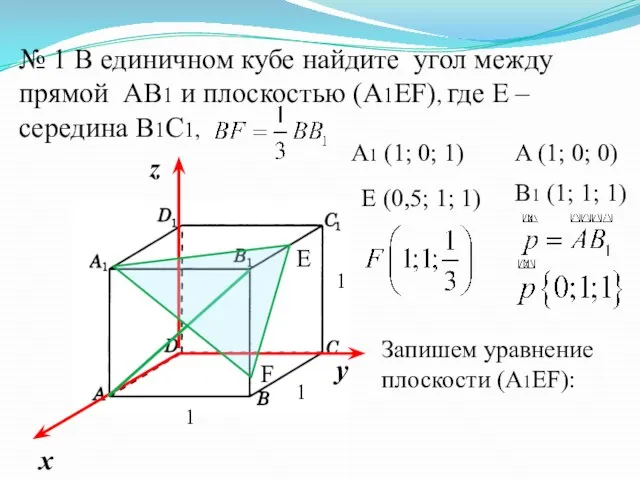
№ 1 В единичном кубе найдите угол между прямой AВ1 и плоскостью (А1EF), где Е – середина В1С1,
1
1
1
F
E
A1 (1; 0; 1)
Е (0,5; 1; 1)
A (1; 0; 0)
B1 (1; 1; 1)
Запишем уравнение плоскости (А1EF):

A1 (1; 0; 1)
Е (0,5; 1; 1)
- уравнение плоскости (А1EF).

- вектор нормали к плоскости
- направляющий вектор прямой
Ответ:

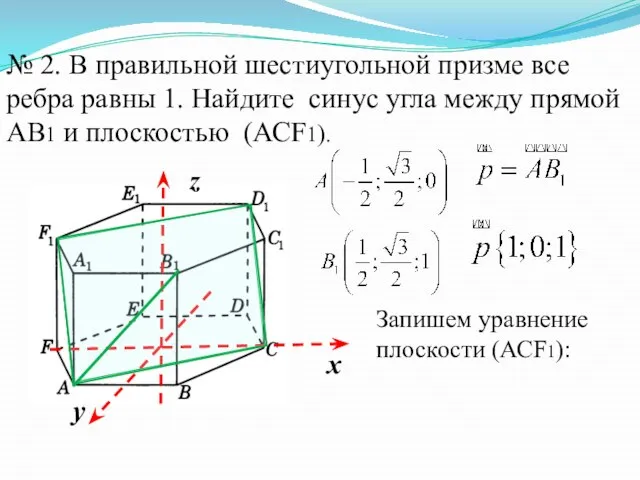
№ 2. В правильной шестиугольной призме все ребра равны 1. Найдите синус угла между прямой AВ1 и плоскостью (АСF1).
Запишем уравнение плоскости (АСF1):

C (1; 0;0)
F1 (- 1; 0;1)
- уравнение плоскости (АСF1).

- вектор нормали к плоскости
- направляющий вектор прямой
Ответ:

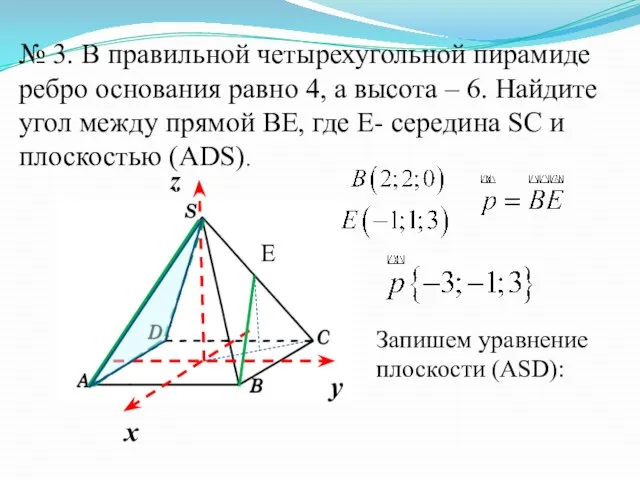
№ 3. В правильной четырехугольной пирамиде ребро основания равно 4, а высота – 6. Найдите угол между прямой ВЕ, где Е- середина SC и плоскостью (АDS).
E
Запишем уравнение плоскости (АSD):

- уравнение плоскости (АSD).

- вектор нормали к плоскости
- направляющий вектор прямой
Ответ:

Угол между плоскостями.

Угол между плоскостями равен углу между
перпендикулярами к этим плоскостям.

Например:

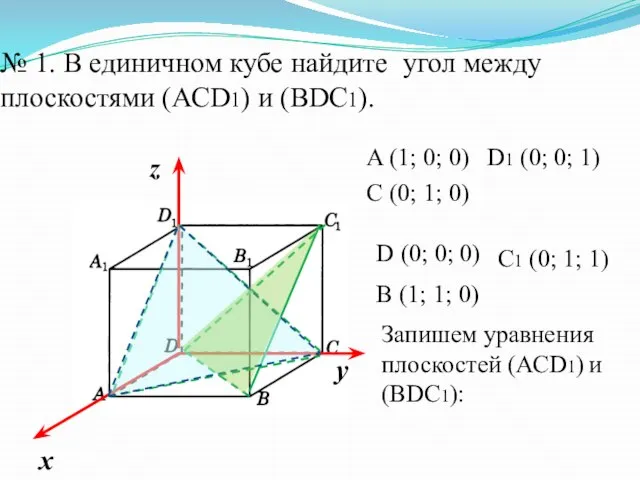
№ 1. В единичном кубе найдите угол между плоскостями (АСD1) и (ВDC1).
A (1; 0; 0)
C (0; 1; 0)
D1 (0; 0; 1)
Запишем уравнения плоскостей (АСD1) и (BDC1):
D (0; 0; 0)
B (1; 1; 0)
C1 (0; 1; 1)

A (1; 0; 0)
C (0; 1; 0)
D1 (0; 0; 1)
D (0; 0; 0)
B (1; 1; 0)
C1 (0; 1; 1)
Ответ:

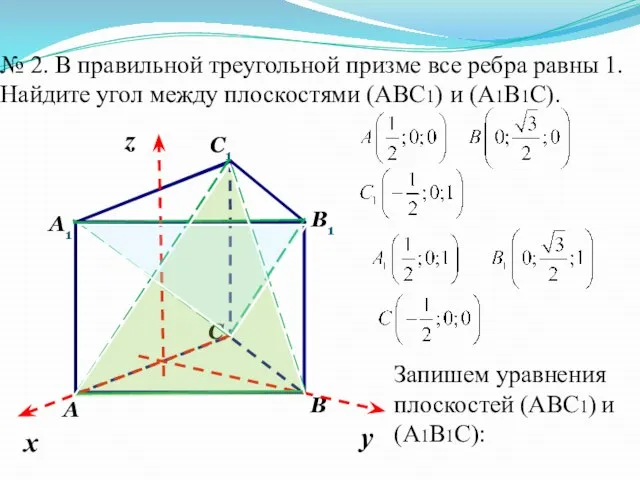
№ 2. В правильной треугольной призме все ребра равны 1. Найдите угол между плоскостями (АВС1) и (А1В1С).
Запишем уравнения плоскостей (АBС1) и (A1B1C):

Ответ:

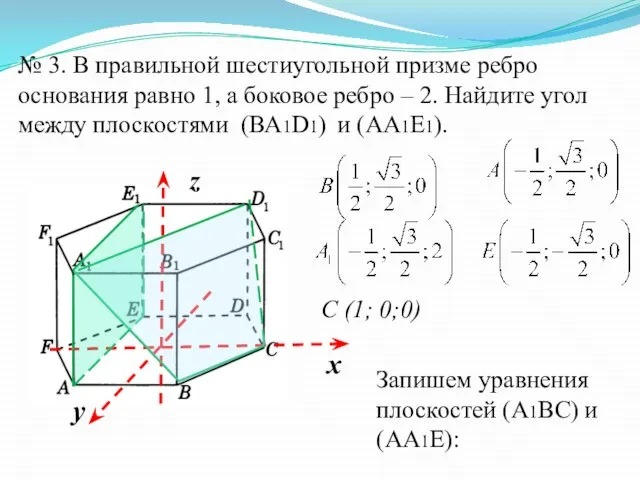
№ 3. В правильной шестиугольной призме ребро основания равно 1, а боковое ребро – 2. Найдите угол между плоскостями (ВА1D1) и (АА1Е1).
C (1; 0;0)
Запишем уравнения плоскостей (А1BC) и (AA1E):

C (1; 0;0)

Ответ: