Тела вращения на примере конуса

Конус в переводе с греческого «konos» означает «сосновая шишка».
С конусом люди знакомы с глубокой древности.
Много сделала для геометрии школа Платона (428–348 гг. до н. э.).
Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса;
б) изучение конических сечений.
Историческая справка о конусе

Большой трактат о конических сечениях был написан Аполлонием Пергским– учеником Евклида, который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
Историческая справка о конусе

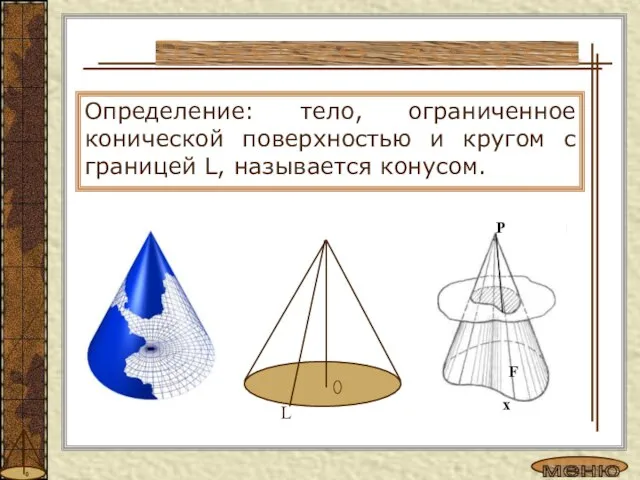
Понятие конуса
Определение: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.

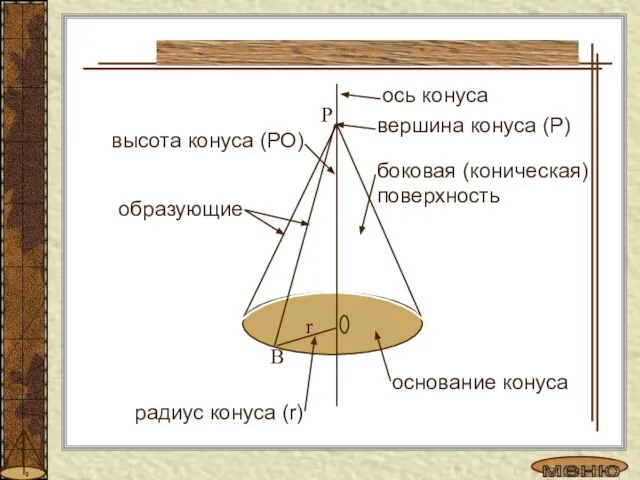
боковая (коническая) поверхность
высота конуса (РО)
ось конуса
вершина конуса (Р)
основание конуса
радиус конуса (r)
Элементы конуса
B
r
образующие
P

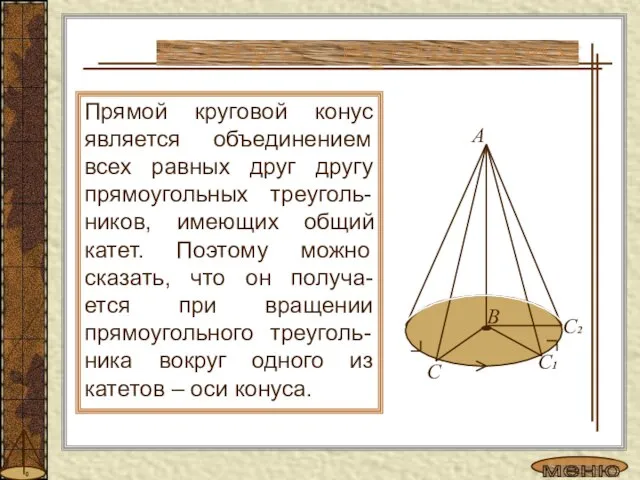
Прямой круговой конус является объединением всех равных друг другу прямоугольных треуголь-ников, имеющих общий катет. Поэтому можно сказать, что он получа-ется при вращении прямоугольного треуголь-ника вокруг одного из катетов – оси конуса.
Конус вращения

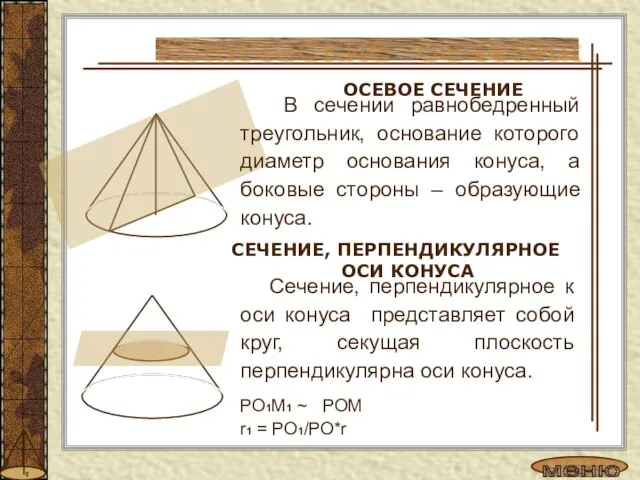
Сечение, перпендикулярное к оси конуса представляет собой круг, секущая плоскость перпендикулярна оси конуса.
РО1М1 ~ РОМ
r1 = РО1/РО*r
ОСЕВОЕ СЕЧЕНИЕ
Конические сечения
СЕЧЕНИЕ, ПЕРПЕНДИКУЛЯРНОЕ ОСИ КОНУСА
В сечении равнобедренный треугольник, основание которого диаметр основания конуса, а боковые стороны – образующие конуса.

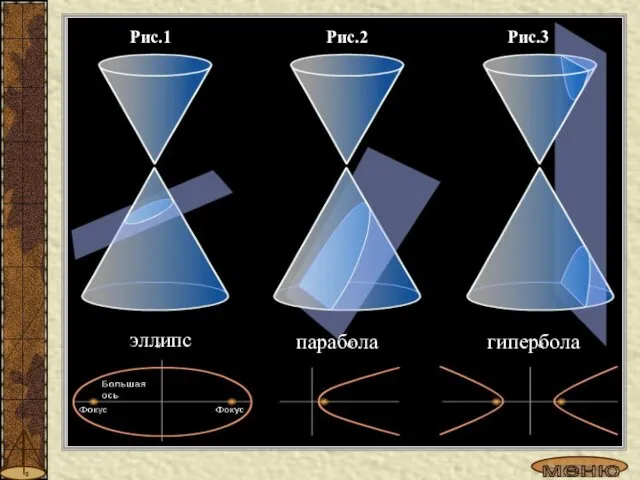
Рис.1
Рис.2
Рис.3
эллипс
парабола
гипербола

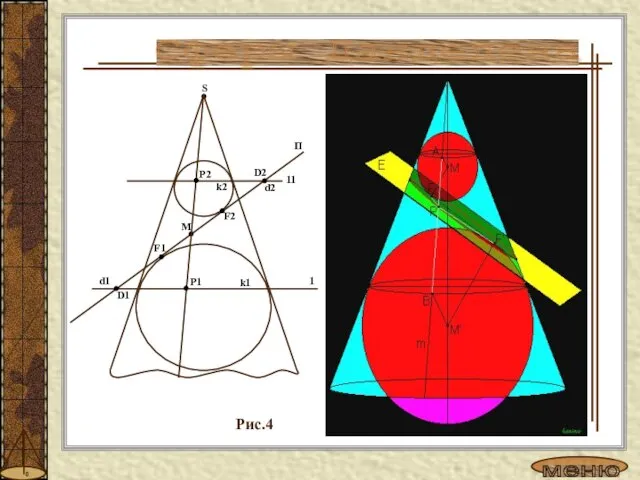
Рис.4
Сферы Данделена

Применение своиств конических сечений

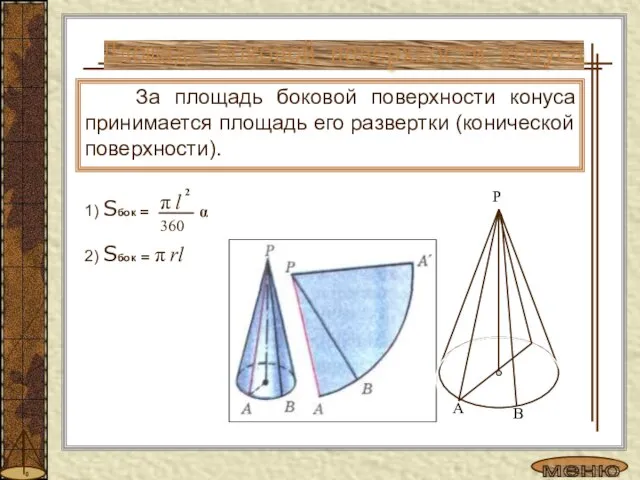
За площадь боковой поверхности конуса принимается площадь его развертки (конической поверхности).
1) Sбок =
Площадь боковой поверхности конуса

Площадь полной поверхности конуса
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.

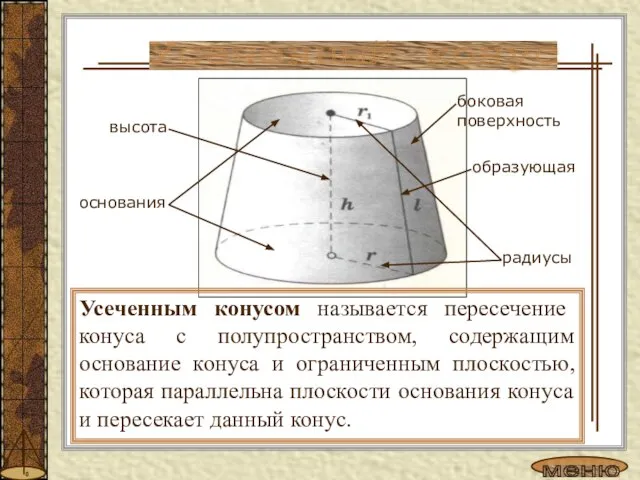
Усеченным конусом называется пересечение конуса с полупространством, содержащим основание конуса и ограниченным плоскостью, которая параллельна плоскости основания конуса и пересекает данный конус.
основания
образующая
радиусы
боковая поверхность
высота
Усеченный конус

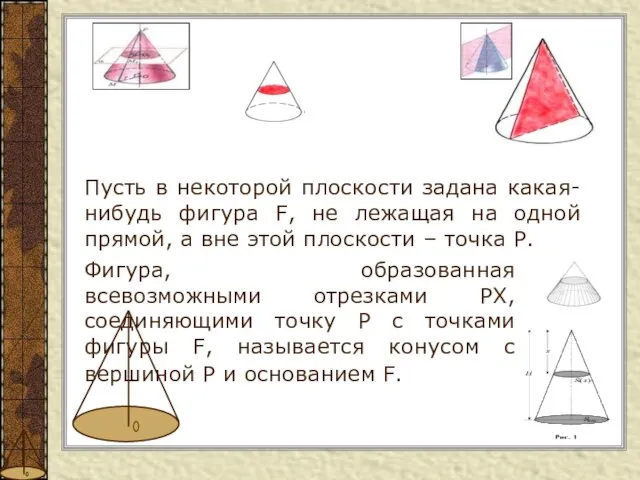
Пусть в некоторой плоскости задана какая-нибудь фигура F, не лежащая на одной прямой, а вне этой плоскости – точка P.
Фигура, образованная всевозможными отрезками PX, соединяющими точку P с точками фигуры F, называется конусом с вершиной Р и основанием F.