Теория графов:подграфы и деревья

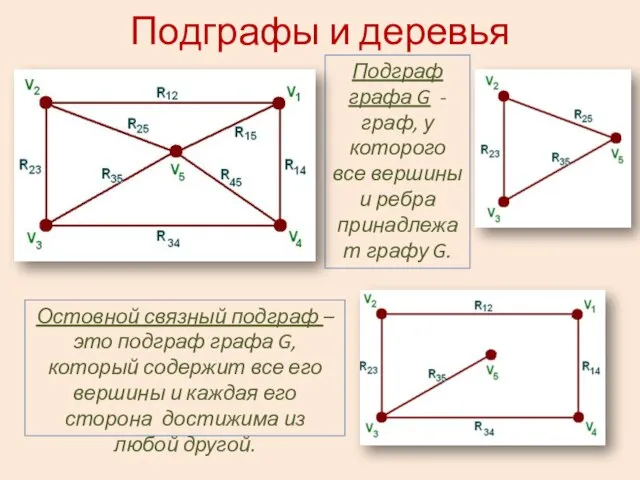
Подграфы и деревья
Подграф графа G - граф, у которого все вершины и ребра принадлежат графу G.
Остовной связный подграф – это подграф графа G, который содержит все его вершины и каждая его сторона достижима из любой другой.

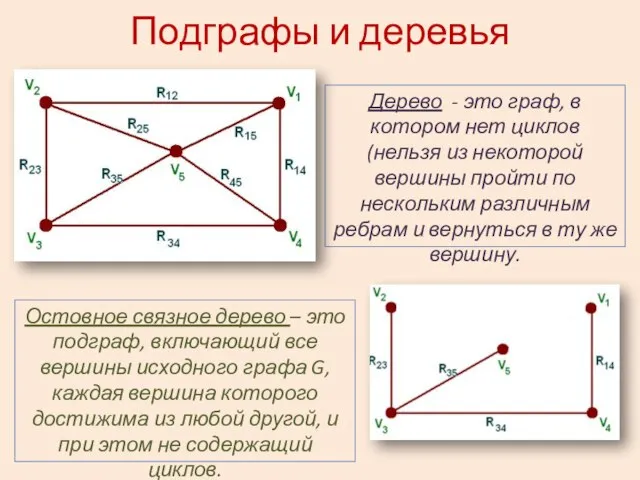
Подграфы и деревья
Дерево - это граф, в котором нет циклов (нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину.
Остовное связное дерево – это подграф, включающий все вершины исходного графа G, каждая вершина которого достижима из любой другой, и при этом не содержащий циклов.

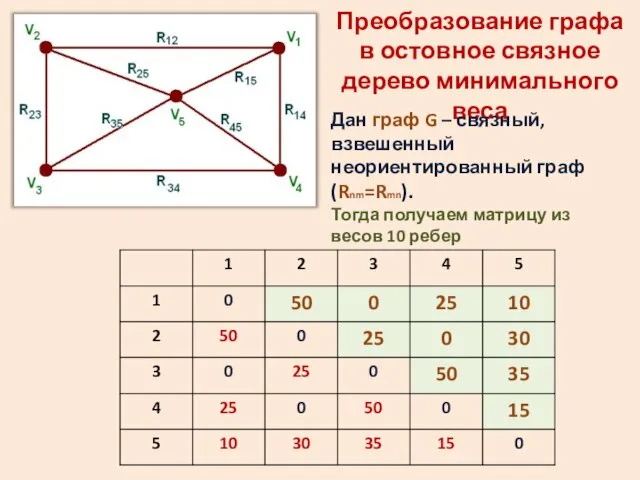
Преобразование графа в остовное связное дерево минимального веса
Дан граф G – связный, взвешенный неориентированный граф (Rnm=Rmn).
Тогда получаем матрицу из весов 10 ребер