Теория принятия решений

Основные понятия и определения
Теория принятия решений − область исследования, использующая понятия и методы математики, статистики, экономики, менеджмента и психологии с целью изучения закономерностей выбора людьми путей решения разного рода задач, а также способов поиска наиболее выгодных из возможных решений.
Принятие решений в профессиональном отношении представляет собой особый вид человеческой деятельности, который состоит в обоснованном выборе наилучшего в некотором смысле варианта или нескольких предпочтительных вариантов из имеющихся возможных.

Люди и их роли в
процессе принятия решений
Лицо, принимающее решения (ЛПР) − человек, фактически осуществляющий выбор наилучшего варианта действий.
Владелец проблемы — человек, который, по мнению окружающих, должен решать данную проблему и несёт ответственность за приня­тые решения.
Руководитель или участник активной группы — группы людей, имеющих общие интересы и старающихся оказать влияние на процесс выбора и его результат.

Эксперт − профессионал в той или иной области, к которому обращаются за оценками и рекомендациями все люди, вовлечённые в процесс принятия решений.
Консультант по принятию решений. Его роль сводится к разумной организации процесса принятия решений: помощи ЛПР и владельцу про­блемы в правильной постановке задачи, выявлении позиций активных групп, организации работы с экспертами.

Альтернативы
Альтернатива − вариант действия.
Альтернативы − неотъемлемая часть проблемы принятия решений: если не из чего выбирать, то нет и выбора.
Альтернативы бывают зависимыми и независимыми.

Независимыми являются те альтернативы, любые действия с которыми (удаление из рассмотрения, выделение в качестве единст­венно лучшей) не влияют на качество других альтернатив.
При зависимых альтернативах оценки одних из них оказывают влияние на качество других.
Наиболее простым примером зависимости является непосредственная групповая зависимость: если решено рассмат­ривать хотя бы одну альтернативу из группы, то надо рассмат­ривать и всю группу.

Критерии
Критерии − показатели привлекательности различных вариантов решений для ЛПР.
Критерии могут быть зависимыми и независимыми.
Предположим, что две сравниваемые альтернативы имеют различные оценки по первой группе критериев и одинаковые по второй группе.
Принято считать критерии зависимыми, если предпочтения ЛПР при сравнении альтернатив меняются в зависимости от значений одинаковых оценок по второй группе критериев.

Шкалы оценок
Шкала порядка — оценки упорядочены по возрастанию или убыванию качества. Примером может служить шкала эко­логической чистоты района около места жительства:
очень чистый район;
вполне удовлетворительный по чистоте;
экологическое загрязнение велико.
Шкала равных интервалов — интервальная шкала. Для этой шкалы имеются равные расстояния по изменению качест­ва между оценками.
Например, шкала дополнительной прибы­ли для предпринимателя может быть следующей: 1 млн, 2 млн, 3 млн и т.д.
Шкала пропорциональных оценок − идеальная шкала. Примером является шкала оценок по критерию стоимости, отсчёт в которой начинается с установленного значения (напри­мер, с нулевой стоимости).

Процесс принятия решений
I этап Поиск информации. Собирается вся доступная на момент принятия решения информация: фактические данные, мнение экс­пертов. Если возможно, строятся математические модели; проводятся социологические опросы; определяются взгляды на проблему со стороны активных групп, влияющих на её ре­шение.

II этап Поиск альтернатив. Заключается в определении того, что можно, а чего нельзя делать в имеющейся ситуации, т. е. с выделением вариантов решений (альтернатив).
III этап Выбор лучшей альтернативы. Включает в себя сравнение альтернатив и выбор наилучшего варианта (или вариантов) решения.

Множество Эджворта-Парето
Назовём альтернативу А доминирующей по отношению к альтернативе В, если по всем критериям оценки альтернативы А не хуже, чем альтернативы В, а хотя бы по одному критерию оценка А лучше. При этом альтернатива В называется доминируемой.

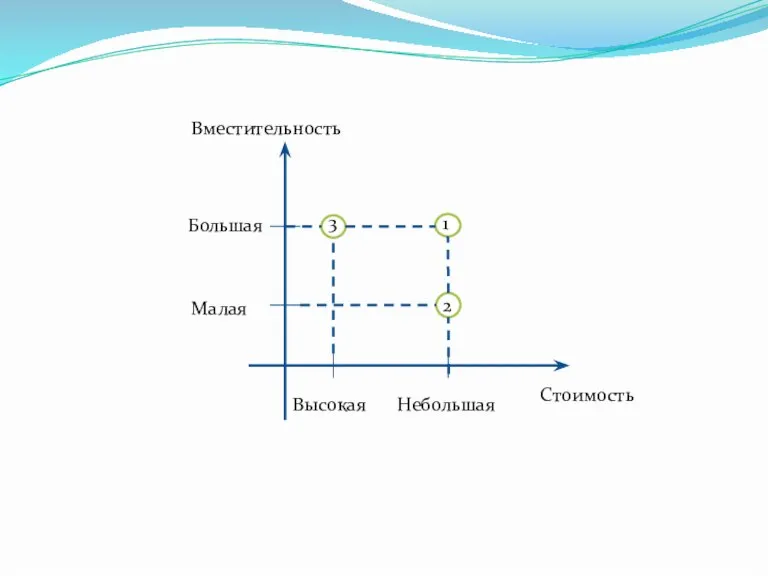
Пример. Предположим, что некоторый человек выбирает автомобиль по двум критериям: стоимость и вместительность салона. Из множества предложенных вариантов он остановился на трёх.

Вместительность
Большая
Малая
Высокая
Небольшая
Стоимость
1
2
3

Предположим, что по какой-то причине покупка Газели невозможна. Тогда альтернативы 2 и 3 не находятся в отношении доминирования. По одному из критериев лучше альтернатива 2, по другому – альтернатива 3.
Предположим, что задана группа альтернатив. Сравним попарно все альтернативы и исключим те из них, которые доминируют хотя бы одной из оставшихся альтернатив. Тогда оставшиеся (недоминируемые) альтернативы принадле-жат множеству Эджворта-Парето (Э-П).

Типовые задачи принятия решений
Основные задачи принятия решений.
1. Упорядочение альтернатив. Для ряда задач возникает потребность определить порядок на множестве альтернатив.
2. Распределение альтернатив по классам решений.
3. Выделение лучшей альтернативы. Эта задача традици­онно считалась одной из основных в принятии решений. Она часто встречается на практике.

Задачи с вазами
Ваза - это непрозрачный сосуд, в котором находится определённое (известное лишь организатору эксперимента) количество шаров различного цвета.
Задачи с вазами типичны для группы наиболее простых задач принятия решений - задач статистического типа.

Типовая задача
Перед испытуемым ставится ваза, ко­торая может быть вазой 1-го или 2-го типа. Даётся следующая информация: сколько имеется у экспериментатора ваз 1-го и 2-го типов; сколько черных и красных шаров в вазах 1-го и 2-го типов; какие выигрыши ожидают испытуемого, если он угадает, какого типа ваза; какие проигрыши ожидают его, если он ошибётся.
После получения такой информации испытуемый должен сделать выбор: назвать, к какому типу принадлежит постав­ленная перед ним ваза.

Пусть, например, экспериментатор случайно выбирает вазу для испытуемого из множества, содержащего 700 ваз 1-го типа и 300 ваз 2-го типа.
Пусть в вазе 1-го типа содержится 6 красных шаров и 4 черных. В вазе 2-го типа содержится 3 красных и 7 черных шаров.
Если перед испытуемым находится ваза 1-го типа и он угадает это, то получит выигрыш 350 д. е., если не угадает, его проигрыш составит 50 д. е.

Если перед ним ваза 2-го типа и он это угадает, то получит выигрыш 500 д. е., если не угадает, его проигрыш составит 100 д. е.
Испытуемый может предпринять одно из следующих действий:
d1 — сказать, что ваза 1-го типа;
d2 — сказать, что ваза 2-го типа.

В теории принятия решений выделяют три класса моделей:
Принятие решений в условиях определённости.
Принятие решений в условиях риска.
Принятие решений в условиях полной неопределённости.
Окружающие условия, обстановка или обстоятельства, в которых необходимо действовать при осуществлении операций, получили название природы.

В моделях в условиях полной определённости имеется несколько альтернатив (их может быть и бесконечно много), а о природе все точно известно и у неё имеется только одно-единственное состояние.
Модели в условиях риска характеризуются наличием нескольких альтернатив и нескольких состояний природы, относительно которых известны вероятности их наступления.
В моделях в условиях полной неопределённости имеется несколько альтернатив и несколько состояний природы, но о вероятностях их наступления ничего неизвестно в принципе.

Платежная матрица

Модели принятия решений в условиях риска

Ожидаемое значение случайной величины

В моделях принятия решений в условиях риска для выбора наилучшего решения используются два критерия (или метода, основанного на критериях):
критерий максимального ожидаемого платежа (выигрыша),
критерий минимального ожидаемого риска.

Модели принятия решений в условиях неопределенности
Примеры неопределенностей, для которых нельзя получить обоснованные значения вероятностей:
спрос и объемы продаж на действительно новую продукцию, которой ранее на рынке не было;
состояние фондового рынка, рынка товаров и услуг, и вообще эконо­мики в будущем (через месяц, год, несколько лет и т. д.);
успех или неуспех новой книги, нового фильма, телепередачи и т. п.;
возникновение природных, социальных и экономических катаклизмов;
молодежные музыкальные течения, и вообще состояние культуры че­рез несколько лет.

Модели принятия решений в условиях неопределенности
Эти задачи имеют место тогда, когда информация, необходимая для принятия решений, является неточной, неполной, неколичественной, а формальные модели исследуемой системы либо слишком сложны, либо отсутствуют.

Методы принятия решений в условиях неопределенности
максиминный критерий (критерий Вальда);
максимаксный критерий;
критерий минимаксного риска (критерий Сэвиджа);
критерий пессимизма-оптимизма (критерий Гурвица).

Максиминный критерий (критерий Вальда)
Критерий позволяет принимать такое решение, которое гарантирует некоторый выигрыш даже при наступлении самого неблагоприятного состояния природы, так что при реализации более благоприятных состояний природы ЛПР получит больший выигрыш.
Применение максиминного критерия оправдано для осторожного, не склонного к риску ЛПР, а также в ситуациях, в которых получение отрицательного результата недопустимо, например, когда речь идет о безопасности людей и их здоровье.

Максимаксный критерий
ЛПР, применяющий максимаксный критерий, склонен к риску и верит, что наступит такое состояние природы, при котором его выигрыш будет наибольшим. Для такого ЛПР выигрыш имеет большую значимость, чем проигрыш (выигрыш — все, проигрыш — ничто).

Критерий минимаксного риска (критерий Сэвиджа)
ЛПР, применяющий критерий Сэвиджа, исходит того, что всегда следует ожидать наступление наихудшего состояния природы, или хотя бы готовиться к нему. Однако в отличие от критерия Вальда, в котором по платежной матрице сначала ищется минимальный платеж, а среди них — максимальный, критерий Сэвиджа оперирует матрицей рисков и в ней сначала определяется максимальный риск, а среди них — минимальный.