Возмущенная зона и поршневая ударная волна впереди СМЕ в нижней короне по данным SDO М.В. Еселевич Институт солн

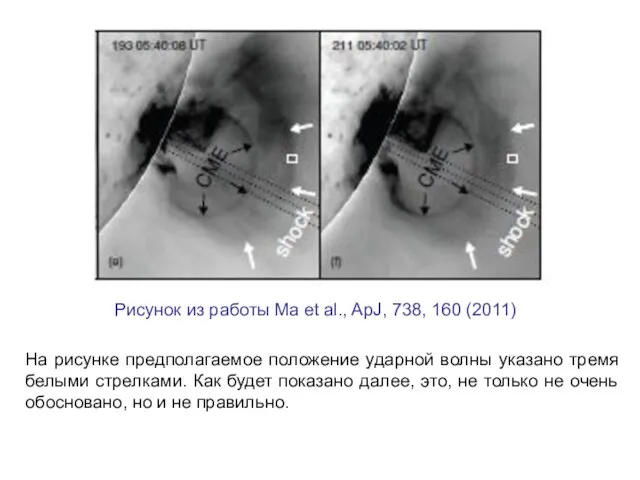
Главная трудность таких исследований – это отождествление и измерение ударного фронта на фоне других, сравнимых по своим пространственным размерам, неоднородностей. Эта проблема до сих пор не решена. Поэтому, практически во всех зарубежных работах ударный фронт перед СМЕ скорее угадывается (не всегда правильно), чем регистрируется. Приведем конкретный пример 13 июня 2010 г. типичного рассмотрения ударной волны перед СМЕ по современным данным инструмента AIA/SDO из статьи Ma et al., ApJ, 738, 160 (2011).

На рисунке предполагаемое положение ударной волны указано тремя белыми стрелками. Как будет показано далее, это, не только не очень обосновано, но и не правильно.
Рисунок из работы Ma et al., ApJ, 738, 160 (2011)

Целью данной работы является регистрация ударного фронта и измерение его ширины в событии 13 июня 2010 г. по данным AIA/SDO. Сопоставление результатов с обобщенными выводами, сделанными ранее для ударных волн на расстояниях 1.5R0 < R < 30R0 в работах [Eselevich, M. and V., 2008; Eselevich, M., 2010].
Событие 13 июня 2010 г. рассмотрено в работах:
Patsourakos S., Vourlidas A., and Stenborg G., ApJ, 724, L188, 2010.
Kozarev K.A. et al., ApJ Lett., 733, L25, 2011.
Ma et al., ApJ, 738, 160, 2011.

Данные анализа
Использовались данные инструмента AIA/SDO,
канал с длиной волны 211Å (FeXIV)
httphttp://http://wwwhttp://www.http://www.lmsalhttp://www.lmsal.http://www.lmsal.comhttp://www.lmsal.com/http://www.lmsal.com/gethttp://www.lmsal.com/get_http://www.lmsal.com/get_aiahttp://www.lmsal.com/get_aia_http://www.lmsal.com/get_aia_datahttp://www.lmsal.com/get_aia_data/
Временное разрешение 12 сек., диапазон расстояний в нижней короне до (1.3-1.4)R0.

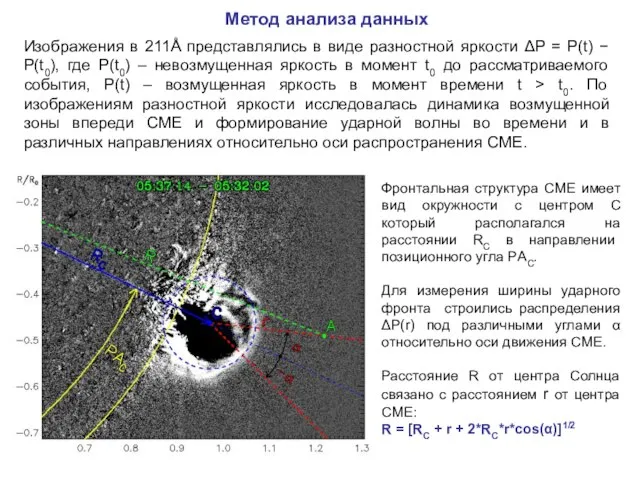
Изображения в 211Å представлялись в виде разностной яркости ΔP = P(t) − P(t0), где P(t0) – невозмущенная яркость в момент t0 до рассматриваемого события, P(t) – возмущенная яркость в момент времени t > t0. По изображениям разностной яркости исследовалась динамика возмущенной зоны впереди CME и формирование ударной волны во времени и в различных направлениях относительно оси распространения СМЕ.
Метод анализа данных
Фронтальная структура СМЕ имеет вид окружности с центром С который располагался на расстоянии RC в направлении позиционного угла РAC.
Для измерения ширины ударного фронта строились распределения ΔP(r) под различными углами α относительно оси движения СМЕ.
Расстояние R от центра Солнца связано с расстоянием r от центра CME:
R = [RC + r + 2*RC*r*cos(α)]1/2

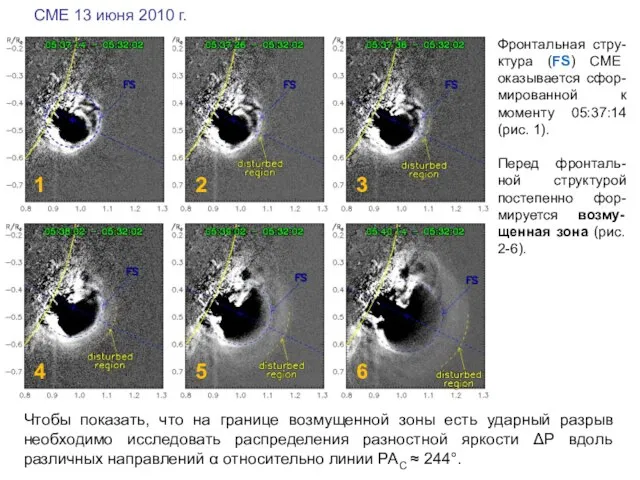
Фронтальная стру-ктура (FS) СМЕ оказывается сфор-мированной к моменту 05:37:14 (рис. 1).
Перед фронталь-ной структурой постепенно фор-мируется возму-щенная зона (рис. 2-6).
1
2
3
4
5
6
Чтобы показать, что на границе возмущенной зоны есть ударный разрыв необходимо исследовать распределения разностной яркости ΔP вдоль различных направлений α относительно линии РАC ≈ 244°.
CME 13 июня 2010 г.

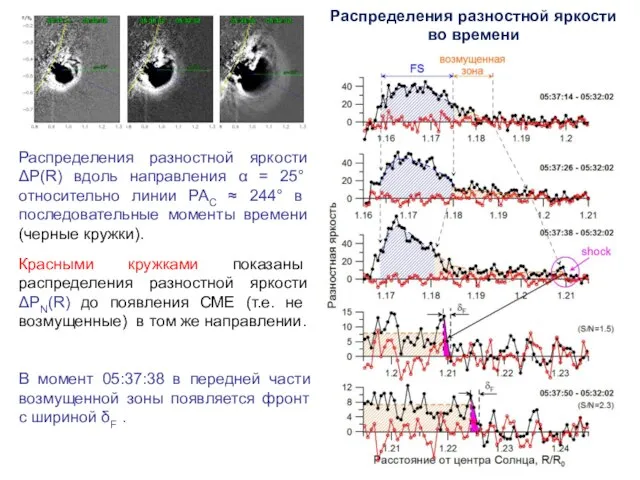
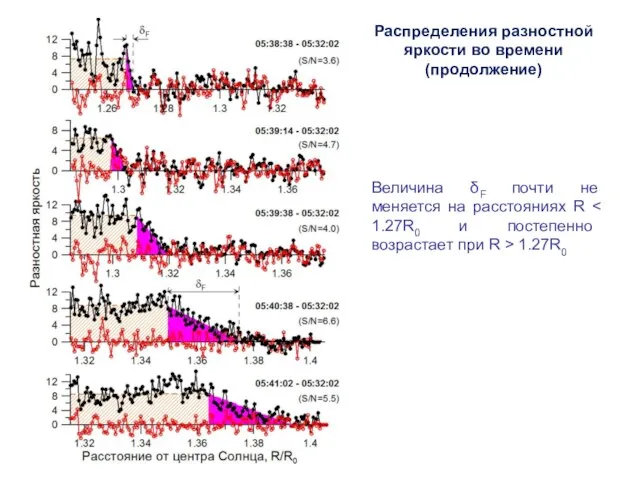
Распределения разностной яркости ΔP(R) вдоль направления α = 25° относительно линии РАC ≈ 244° в последовательные моменты времени (черные кружки).
Красными кружками показаны распределения разностной яркости ΔPN(R) до появления СМЕ (т.е. не возмущенные) в том же направлении.
Распределения разностной яркости во времени
В момент 05:37:38 в передней части возмущенной зоны появляется фронт с шириной δF .

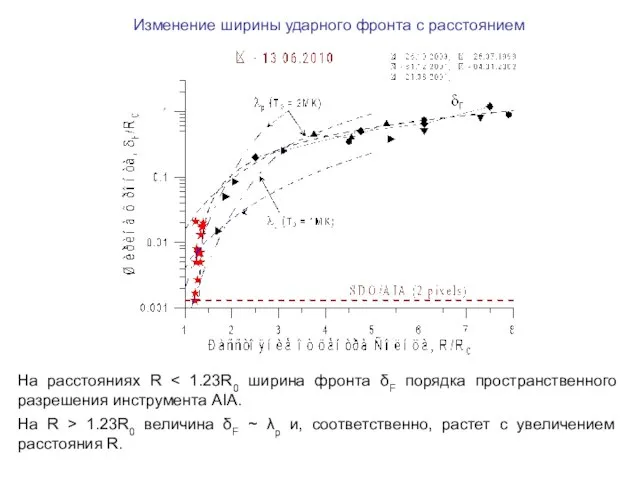
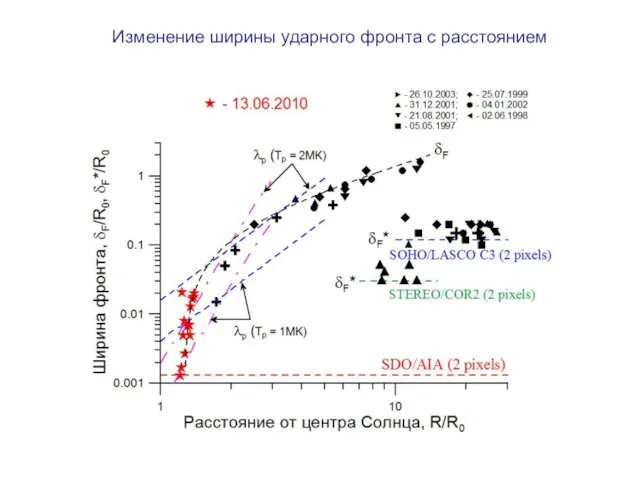
Величина δF почти не меняется на расстояниях R < 1.27R0 и постепенно возрастает при R > 1.27R0
Распределения разностной яркости во времени (продолжение)

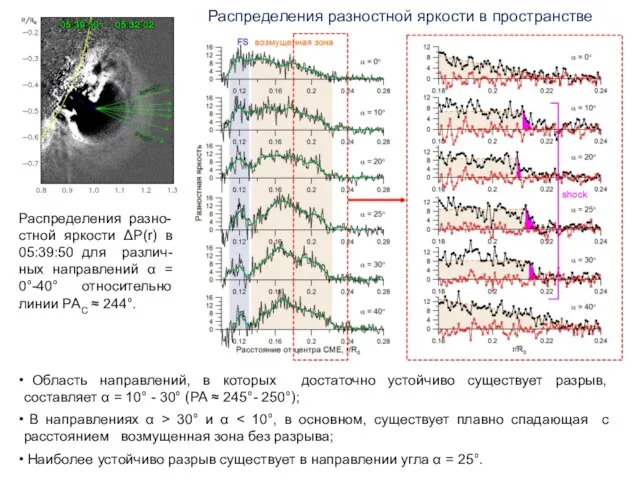
Распределения разно-стной яркости ΔP(r) в 05:39:50 для различ-ных направлений α = 0°-40° относительно линии РАC ≈ 244°.
Распределения разностной яркости в пространстве
Область направлений, в которых достаточно устойчиво существует разрыв, составляет α = 10° - 30° (РА ≈ 245°- 250°);
В направлениях α > 30° и α < 10°, в основном, существует плавно спадающая с расстоянием возмущенная зона без разрыва;
Наиболее устойчиво разрыв существует в направлении угла α = 25°.

По изображениям разностной яркости, практически, невозможно отличить границу плавно спадающей разностной яркости возмущенной зоны от случаев с разрывом на границе. Показать разрыв можно только с использованием изложенной выше методики, которая связана с получением профилей ΔP(r) и сравнением их с профилем “шума“ ΔPN(r).

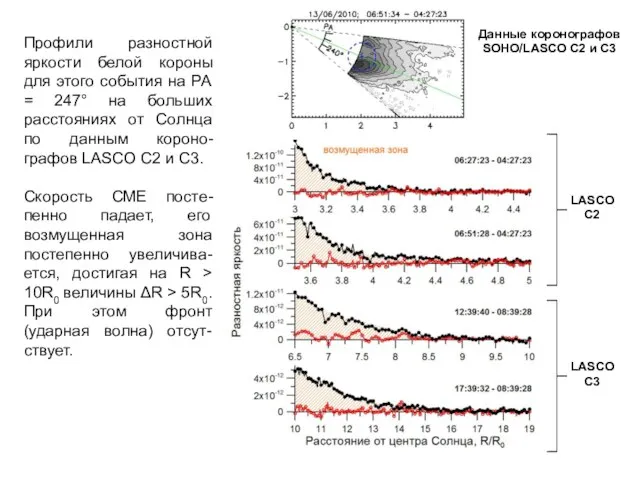
Профили разностной яркости белой короны для этого события на РА = 247° на больших расстояниях от Солнца по данным короно-графов LASCO С2 и С3.
Cкорость СМЕ посте-пенно падает, его возмущенная зона постепенно увеличива-ется, достигая на R > 10R0 величины ΔR > 5R0. При этом фронт (ударная волна) отсут-ствует.
LASCO
C2
LASCO
C3
Данные коронографов
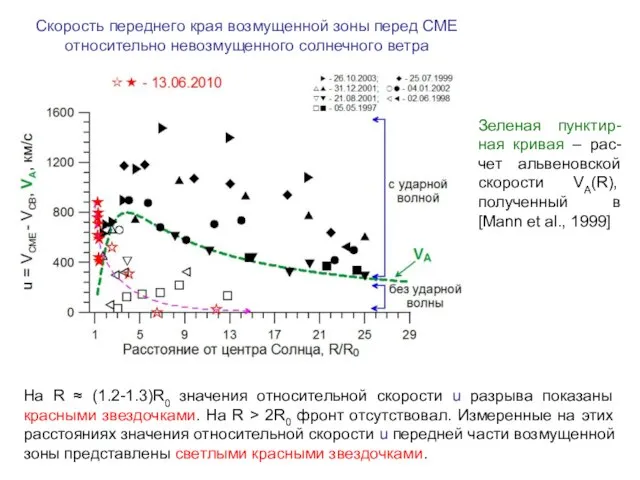
SOHO/LASCO C2 и C3

Зеленая пунктир-ная кривая – рас-чет альвеновской скорости VA(R), полученный в [Mann et al., 1999]
На R ≈ (1.2-1.3)R0 значения относительной скорости u разрыва показаны красными звездочками. На R > 2R0 фронт отсутствовал. Измеренные на этих расстояниях значения относительной скорости u передней части возмущенной зоны представлены светлыми красными звездочками.
Скорость переднего края возмущенной зоны перед CME относительно невозмущенного солнечного ветра

На расстояниях R < 1.23R0 ширина фронта δF порядка пространственного разрешения инструмента AIA.
На R > 1.23R0 величина δF ~ λp и, соответственно, растет с увеличением расстояния R.
Изменение ширины ударного фронта с расстоянием

Выводы
В событии 13 июня 2010 г., исследованного по данным AIA/SDO, показано, что впереди фронтальной структуры СМЕ, постепенно возникает возмущенная зона, размер которой увеличивается по мере удаления СМЕ от Солнца. Ударный разрыв формируется в передней части возмущенной зоны только в очень узком диапазоне углов РА ≈ 245°-250°. Он по своим характеристикам удовлетворяет поршневой столкновительной ударной волне. В остальных направлениях относительно оси движения СМЕ (РА<245° и РА>250°) существует только возмущенная зона и устойчивый разрыв отсутствует.
Анализ СМЕ 13 июня 2010 г. подтвердил ранее установленные законы формирования поршневой ударной волны перед СМЕ, которые сводятся к следующему:
а) Формирование ударной волны перед СМЕ в некоторой окрестности вдоль оси его распространения определяется выполнением локального неравенства u(R) > VА(R) и может осуществляться на различных расстояниях от Солнца.
б) На расстояниях R < (6-8)R0 ширина ударного фронта δF порядка длины свободного пробега протонов λp и механизм диссипации энергии во фронте столкновительный.

Спасибо за внимание!

Изменение ширины ударного фронта с расстоянием