Методы решения квадратных уравнений

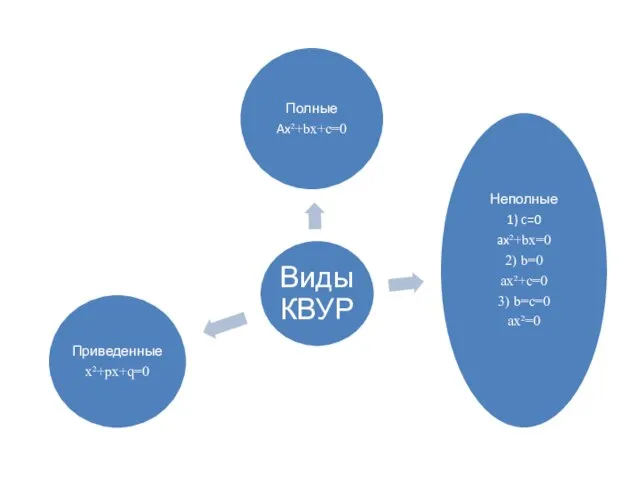
Определение
Квадратные уравнения (КВУР) – уравнения вида ax²+bx+c=0, где x – переменная, a, b и c – любые числа, причем a≠0.
(В случае, когда а = 0, КВУР переходит в класс линейных уравнений, т.к. исключается переменная во второй степени)

Методы решения.
Неполные КВУР.
I. ax²+bx=0
1) Вынести общий множитель за скобки и разложить на множители:
x·(ax+b)=0
x=0 или ax+b=0

Методы решения.
Неполные КВУР.
1) 2x²+3x=0
x(2x+3)=0
x=0 или 2x+3=0
2x=-3
x=-1,5
Ответ: -1,5; 0
2) 5u²-4u=0
u(5u-4)=0
u=0, u=0, u=0,
5u-4=0; 5u=4; u=0,8.
Ответ: 0; 0,8.
Примеры:

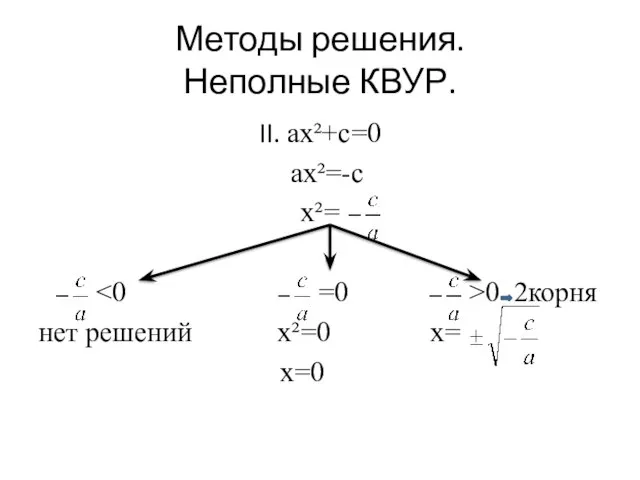
Методы решения.
Неполные КВУР.
II. ax²+c=0
ax²=-c
x²=
˂0 =0 ˃0 2корня
нет решений x²=0 x=
x=0

Методы решения.
Неполные КВУР.
Примеры:
x²+19=0
x²=-19
-19˂0 нет корней
Ответ: нет корней.
Примеры:
2) x²-19=0
x²=19
19˂0 2 корня
x=
x=
Ответ: .

Методы решения.
Неполные КВУР.
III. ax²=0
x²=0 смотри здесь.
x=0

Методы решения.
Выделение полного квадрата.
b=четное
x²-4x+3=0
x²-2·x·2+4-4+3=0
(x-2)²-1=0
(x-2)²=1
x-2=±
x-2=
x=3 или x=1
Ответ:1, 3.
b=нечетное
2x²+x+2=0 | :2
x²+ x+1=0
x²+2·x· + - +1=0
(x+0,25)²+ =0
(x+0,25)²= -
˂0 =˃ нет корней
Ответ: нет корней.

Методы решения.
Полные КВУР ax²+bx+c=0
Формула полного квадрата:
x²+8x+16=0
(x+4)²=0
x+4=0
x=-4
Ответ: x=-4.
2) a²-2,6a+1,69=0
(a-1,3)²=0
a-1,3=0
a=1,3
Ответ: a=1,3.

Методы решения.
Полные КВУР. Частные случаи.
Теорема 1:
Если a+b+c=0, то
x =1, x =
Примеры:
5x²-8x+3=0
5-8+3=0 Теорема1
x =1; x = .
Ответ: x =1; x = .
2) 3x²-7x+4=0;
3-7+4=0 Теорема1
x =1; x = .
Ответ: 1; .

Методы решения.
Полные КВУР. Частные случаи.
Теорема 2:
Если a-b+c=0, то
x =-1, x =- .
Примеры:
1) 5x²+9x+4=0
5-9+4=0 Теорема2
x =-1; x =- .
Ответ: x =-1; x =- .
2) y²-22y-23=0
1+22-23= 0 Теорема2
x =-1; x =-
x =23.
Ответ:-1; 23.

Методы решения.
Приведенные КВУР.
Теорема ВИЕТА:
x²+px+q=0 (a=1)
x1 +x2 =-p
x *x =q
Примеры:
x²-6x+8=0
x =2; x =4 x +x =6
x +x =8
Ответ: 2, 4.
y²-10y-24=0
y =-4; y =6 y +y =10
y *y =24
Ответ: y =-4; y =6.

Методы решения.
«Переброска»
1) 2x²-5x-3=0
x²-5x-3*2=0
x²-5x-6=0 (решим по Теореме 2)
Корни запишем в виде: x =
x = =3
Ответ: x =-0,5; x =3.
2) 3x²+2x-5=0
x²+2x-15=0
Решим по Теореме ВИЕТА.
x =
x =
Ответ: ;

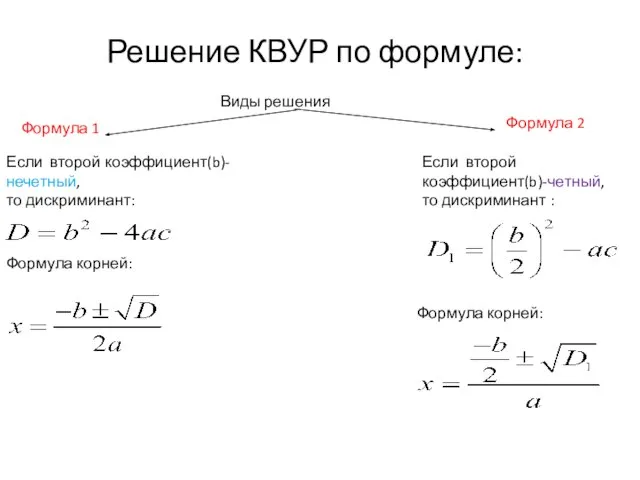
Решение КВУР по формуле:
Виды решения
Формула корней:
Если второй
коэффициент(b)-четный,
то дискриминант :
Формула корней:
Если второй коэффициент(b)-нечетный,
то дискриминант:
Формула 1
Формула 2

Решим примеры
1)
a=4;b=1;c=-33
Т.к. b-нечетное, то решаем это уравнение по формуле 1:
Корни:
Ответ:-3;
=
=
=

2)
a=3;b=-13;c=14
Т.к. b-нечетное, то решаем по формуле 1:
Корни:

a=12;b=16;c=-3
Т.к. b-четное, то решаем по формуле 2:
3)
Корни:

4)
a=5;b=26;c=-24
Т.к. b-четное, то решаем по формуле 2:
Корни: