11 класс учитель Чепаева М. И. МОУ «Пичпандинская средняя школа»

Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце 17 столетия. Тем более поразительно, что за долго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, но и сумел найти максимум функции f(x)= х2(а -х)
В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной.
Историческая справка

Различные варианты изложения, приме-
нённые к разным задачам, встречаются
уже у Р. Декарта, французского математи-
ка Роберваля (1602 -1675 ) английского
Учёного Д.Грегори (1638 -1675), в работе
И. Барроу (1630 -1677)
Систематическое учение о производных
развито Лейбницем и Ньютоном, который
сформулировал и две основные пробле-
мы анализа:

«1. Длина проходимого пути постоянно дана; требуется найти скорость движения
в предложенное время пути.
2.Скорость движения постоянно дана; требуется найти длину пройденного в предложенное время пути».
Первая проблема задаёт программу развития дифференциального исчисления.
Вторая относится к интегральному исчислению.
На первый вопрос вы знаете ответ, а на второй узнаете изучив следующую главу.

Знаешь ли эти формулы?
(f(x)+g(x))|
(ex ) | ( ax )|
(f(x)*g(x))|
(ap ) |
(kx+b)|
(logax)|
(sin (kx +b))|
(cos (kx+b))|

1.Найти производную функции.
а)ех+х2 б)е-3х в)е 1-х - х-3 г)2х - х-2
2.Найти угловой коэффициент касательной к графику функции у=х2-3 с абсциссой х0= 5
3.Найдите стационарные точки для функции у=2х; у=х2; у=sinx
Выполните устно

1.Если производная функции положительна на промежутке, то функция …
2.Если производная функции отрицательна на промежутке, то функция …
3.Критические точки - это точки ….
4.Промежутки монотонности это ….
5.Если производная функции при переходе через стационарную точку меняет знак с «+» на «-», то….
а если с «-» на «+» то…..
6.Уравнение касательной имеет вид …..
7.Геометрический смысл производной состоит в том, что …
Продолжи утверждение

1.В точке возрастания функции её производная больше нуля.
2.Если производная функции в некоторой точке равна нулю, то в этой имеется экстремум.
3.Производная произведения равна произведению производных.
4.Наибольшее и наименьшее значение функции на некотором отрезке наблюдаются или в стационарных точках, или на концах отрезка.
5.Любая точка экстремума является критической.
верно ли ?.

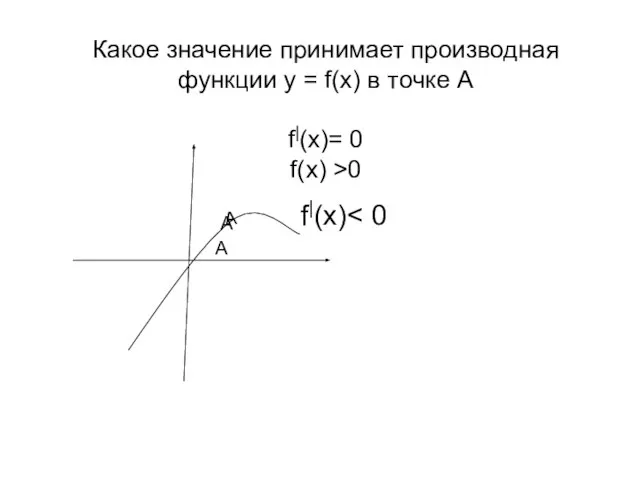
Какое значение принимает производная функции у = f(x) в точке А
f|(x)= 0
f(x) >0
А
А
А
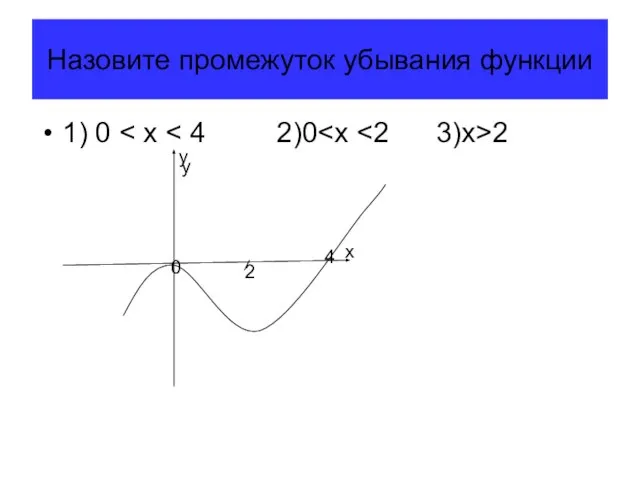
f|(x)< 0

Назовите промежуток убывания функции
1) 0 < x < 4 2)0
2
2
x
y
y
4
0

Выполни эскиз графика функции.
1.Область определения [ -4; 3 ]
2.Множество значений [ -4; 2 ]
3.Производная положительна (-4; 1)
4.Производная отрицательна (1; 3)
5.Нули функции: -2 и 2

И
И
1.Изобрази схематически график какой либо функции, для которой:
.х= -3 точка максимума, х=4 точка минимума.
2. имеет две точки максимума и одну точку минимума.

А1Найти производную функци у=3х4-sinх+5
1)12х3-cos х 2)4х3+cosx 3)12x3+cosx +5
А2. Какие из данных функций возрастают на всей области определения:
1)у= -3х+1; 2) у=-3х2; 3)у=х2 +1; 4)у=6х;
А3.Какая из функций имеет точки экстремума:
1)у=2х; 2)у=7-5х; 3) у=х3+2х; 4)у=х2+1;
А4 Дано f(x)=(3+4x)(4x-3). Найти f/(-1)
1) -32; 2) 32; 3) -50; 4)50;
А5 Дано х(t)=13t2+2t+1; t=2. Найти V
1) 36; 2)57; 3)54; 4)38
Выполни тест