Содержание
- 2. Карл Гаусс (1777 – 1855) Математический талант Гаусса проявился ещё в детстве. По легенде, школьный учитель
- 3. Найти сумму первых 100 натуральных чисел S – сумма S= 1 + 2 +3+…+98+99+100 S=100+99+98+…+ 3
- 4. Найти сумму первых 10 натуральных чисел. 1+2+3+4+5+6+7+8+9+10= = 55 1 + 10 2 10 =
- 5. Sn – сумма первых n членов арифметической прогрессии …………………………………………………………………………………………………………………………
- 6. n : 2
- 7. Найдите сумму первых сорока членов последовательности, заданной формулой: Решение
- 8. Найдём сумму первых тридцати членов арифметической прогрессии 4; 5,5;… Решение 4, d = 1,5 772,5 Ответ:
- 9. Найдите сумму всех натуральных чисел, не превосходящих 150, которые не делятся на 5. Задача 19. ГИА
- 10. № 690(в) Найдите сумму всех натуральных чисел, кратных 3, заключенных в промежутке от 100 до 200.
- 11. № 691(б) Найдите сумму натуральных чисел больших 50, но меньших 150 и не кратных 5? Решение
- 12. , где 51, 149, n = 149 – 50 = 99 9 900 Последовательность чисел: 55;
- 14. Скачать презентацию




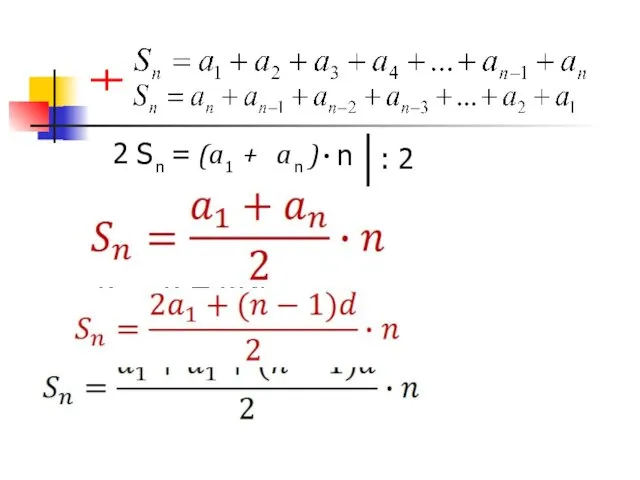






 Стандартный вид числа
Стандартный вид числа Презентация на тему Классификация государственных служащих
Презентация на тему Классификация государственных служащих  Прогрессия - движение вперёд !
Прогрессия - движение вперёд ! Свойства арифметического корня П-ОЙ степени
Свойства арифметического корня П-ОЙ степени Пропорция
Пропорция Презентация на тему Графики функций синуса и косинуса и их свойства
Презентация на тему Графики функций синуса и косинуса и их свойства Презентация на тему Материальная ответственность
Презентация на тему Материальная ответственность  Алгебра. Теоретический материал
Алгебра. Теоретический материал Презентация на тему Природа и общество в философии
Презентация на тему Природа и общество в философии Степенная функция 9 класс учитель Ладошкина И.А.
Степенная функция 9 класс учитель Ладошкина И.А.  Определение квадратного уравнения. Неполные квадратные уравнения
Определение квадратного уравнения. Неполные квадратные уравнения Функции и графики
Функции и графики Преобразования графиков функций 10 класс
Преобразования графиков функций 10 класс Дробные рациональные уравнения
Дробные рациональные уравнения Логарифмическая функция и её приложения Шагаева А.Б. МОУ «Барагашская СОШ» 11 класс
Логарифмическая функция и её приложения Шагаева А.Б. МОУ «Барагашская СОШ» 11 класс  Презентация на тему Верование Восточных славян
Презентация на тему Верование Восточных славян  Решение неравенств с одной переменной Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная шко
Решение неравенств с одной переменной Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная шко Презентация на тему Категории материи
Презентация на тему Категории материи  Pryamaya-proporcionalnost.ppt
Pryamaya-proporcionalnost.ppt Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. Сложение чисел с разными знаками
Сложение чисел с разными знаками Неполные квадратные уравнения
Неполные квадратные уравнения Теорема Виета (8 класс)
Теорема Виета (8 класс) Функция y = x^2
Функция y = x^2 Презентация на тему Использование нормирования
Презентация на тему Использование нормирования КОВАЛЕВСКАЯ Софья Васильевна
КОВАЛЕВСКАЯ Софья Васильевна Методы решения систем линейных уравнений 1- ой степени
Методы решения систем линейных уравнений 1- ой степени Решение линеиных неравенств
Решение линеиных неравенств