Слайд 6 Теорема Виета
Сумма корней приведённого квадратного уравнения равна
второму коэффициенту, взятому с
противоположным

знаком, а
произведение корней равно
свободному члену.
Слайд 7 Доказательство:
рассмотрим приведённое квадратное уравнение

Слайд 8Найдём сумму и произведение корней

Слайд 10Пример 1: Найдём сумму и произведение
корней уравнения

Слайд 12Пример: Найдём подбором корни уравнения

Слайд 13По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше,

скажи постоянства такого:
Умножишь ты корни – и дробь уж готова.
В числителе с, в знаменателе а.
А сумма корней также дроби равна.
Хоть с минусом дробь, что за беда!
В числителе в, в знаменателе а.
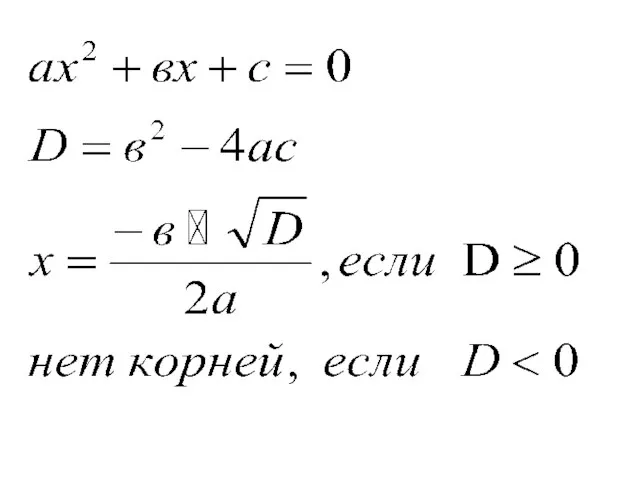
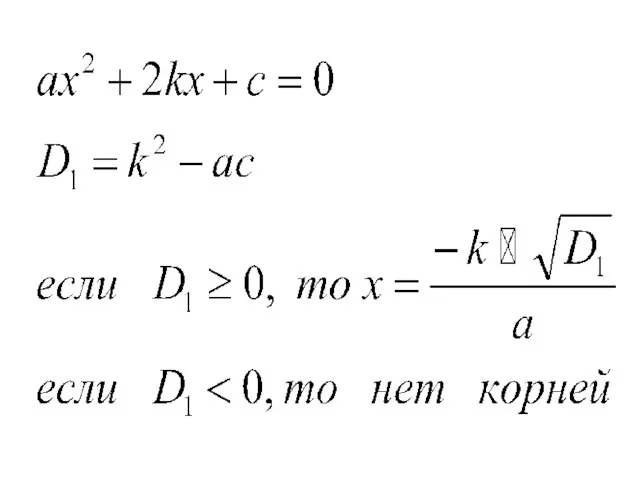





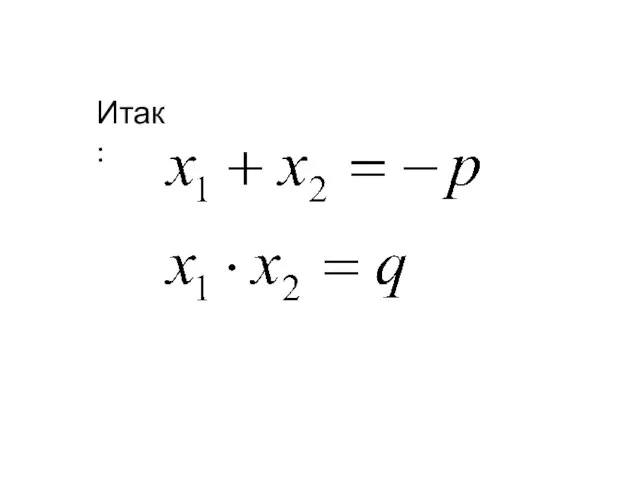




 Презентация на тему Экзамен без стресса
Презентация на тему Экзамен без стресса  Методы решения уравнений
Методы решения уравнений Презентация на тему Российская Федерация, субъекты Российской Федерации и муниципальные образования как субъекты предпринимател
Презентация на тему Российская Федерация, субъекты Российской Федерации и муниципальные образования как субъекты предпринимател Неравенства
Неравенства Алгебра высказываний. Основные операции алгебры высказываний
Алгебра высказываний. Основные операции алгебры высказываний Дифуры 1го порядка
Дифуры 1го порядка Презентация на тему Требования к гос. служащим
Презентация на тему Требования к гос. служащим  Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.
Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.  Технологии промысловой подготовки нефти и газа
Технологии промысловой подготовки нефти и газа Первообразная Правила нахождения первообразных
Первообразная Правила нахождения первообразных  Квадратные уравнения и уравнения, приводимые к квадратным
Квадратные уравнения и уравнения, приводимые к квадратным Функции. Графики функций 7 класс
Функции. Графики функций 7 класс Презентация на тему Театр в 18 веке в России
Презентация на тему Театр в 18 веке в России  Способы задания последовательностей
Способы задания последовательностей  Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. «Арифметическая и геометрическая прогрессии» урок алгебры в 9 классе
«Арифметическая и геометрическая прогрессии» урок алгебры в 9 классе  Исследование математических моделей
Исследование математических моделей Арифметика десятичных дробей
Арифметика десятичных дробей Презентация на тему Структура, полномочия и компетенция арбитражных судов федеральных округов РФ (арбитражных кассационных судов
Презентация на тему Структура, полномочия и компетенция арбитражных судов федеральных округов РФ (арбитражных кассационных судов Логарифмические неравенства
Логарифмические неравенства Решение неравенств с одной переменной и решение систем неравенств
Решение неравенств с одной переменной и решение систем неравенств Презентация на тему где обитают живые организмы 3 класс
Презентация на тему где обитают живые организмы 3 класс  Решение линейных и квадратных уравнений с параметрами в курсе математики основной школы
Решение линейных и квадратных уравнений с параметрами в курсе математики основной школы Линейная функция и ее график 7 класс
Линейная функция и ее график 7 класс Закрепление основных разделов из курса «Алгебра и начала анализа. 10 – 11 класс»
Закрепление основных разделов из курса «Алгебра и начала анализа. 10 – 11 класс» Тригонометрические уравнения Автор: Серебрянская Л. А.
Тригонометрические уравнения Автор: Серебрянская Л. А. Функция y = k√x . Подкоренная функция
Функция y = k√x . Подкоренная функция Последовательности 2011 Васильева Е.Е.
Последовательности 2011 Васильева Е.Е.