Методы решения уравнений

Результат учения равен
произведению способности на старательность.
Если старательность равна нулю,
то и все произведение равно нулю.
А способности есть у каждого.

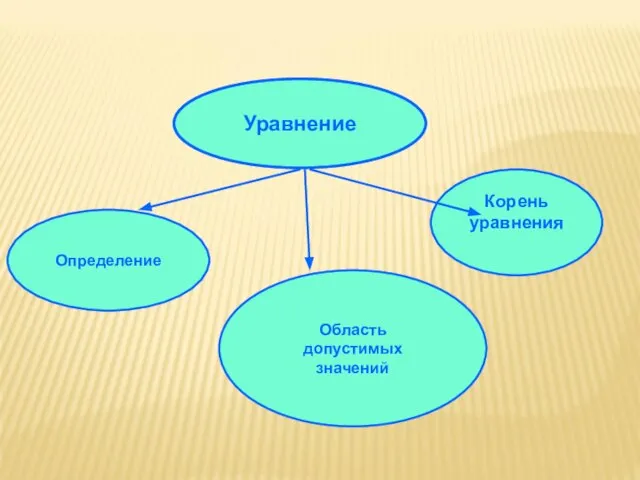
Уравнение
Определение
Область
допустимых значений
Корень уравнения

Устно.
Решить уравнение.

ОТВЕТЫ:
1) х=-2;
2) решений нет;
3) х=1;
4) нет корней;

Найти область допустимых значений уравнений.

ОТВЕТЫ:
-2≤Х ≤2;
2) любое число;
3) любое число, кроме ¾;
4) х>5, кроме 6.

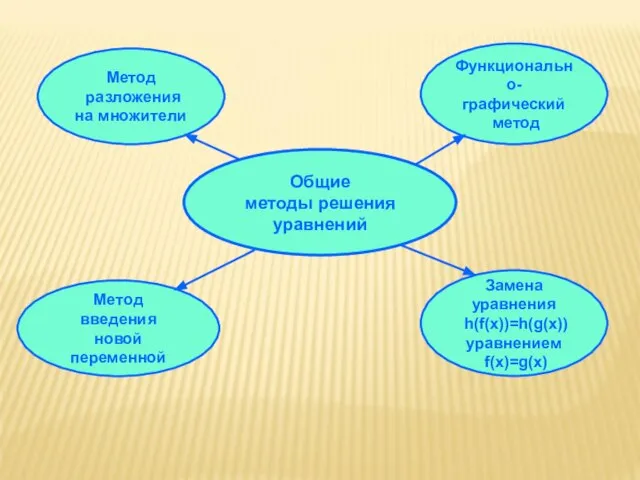
Общие
методы решения уравнений
Метод
разложения
на множители
Метод
введения
новой
переменной
Замена уравнения
h(f(х))=h(g(х))
уравнением
f(х)=g(х)
Функционально-
графический
метод

ОТВЕТЫ:
1) Замена уравнения h (f ( x )) = h (g ( x ), уравнением f (x) = g(x).
2) Функционально-графический.
3) Замена уравнения h (f ( x )) = h (g ( x )), уравнением f (x) = g(x).
4) Замена уравнения h (f ( x )) = h (g ( x )), уравнением f (x) = g(x).
5) Перенести правый член уравнения в левую с противоположным знаком, преобразовать левую часть с помощью формул тригонометрии.
6) Метод разложения на множители.
7) Замена уравнения h (f ( x )) = h (g ( x )), уравнением f (x) = g(x).
8) Метод разложения на множители.
9) Метод введения новой переменной.
10) Метод введения новой переменной.
11) Функционально-графический.
12) Замена уравнения h (f ( x )) = h (g ( x ), уравнением f (x) = g(x).

самостоятельная работа.

I уровень.
Вариант №1.
Решите уравнения.
1.
2.
3.
4.
II уровень. II уровень.
Вариант №1. Вариант №2.
Решите уравнения. Решите уравнения.
1.
2.
3.
4.
I уровень.
Вариант №2.
Решите уравнения.
1.
2.
3.
4.
1.
2.
3.
4.

Ответы.
I уровень.
Вариант №1
Вариант №2
IIуровень.
Вариант №1.
Вариант №2.

Нестандартные уравнения.
1.
0
2
2
-1
0
Решение. ОДЗ.
ОДЗ этого уравнения состоит из двух чисел х=2 и х=0.
Подставив данные значения в исходное уравнение получим,
х=2 корень данного уравнения.
Ответ: 2

2.
log22(х3+х2+5)=0.
Решение.
Так как левая часть является суммой двух
неотрицательных слагаемых, то
х3+х2+5=1.
Решаем первое уравнение системы.
х2(х+2)-(х+2)=0,
(х+2)(х2-1)=0,
х1=-2; х2=-1; х3=1.
Подставляем найденные значения во второе
уравнение системы.
Если х=-2, то -8+2+5=1.
Если х=-1, то -1+1+5=1.
Если х=1, то 1+1+5=1.
Ответ: -2.

Найдите целочисленный корень уравнения:
10х-24-х2
log2(7+6х-х2)- log2(х-2)
=2
1.
log12(6+5х-х2)
Х2-9х+20
=2
2.
Ответ: 1) 5; 2) 3.