Содержание
- 2. Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a 0 b x y=f(x) y
- 3. y=f(x) непрерывная f(x)≤0 на [a; b] a 0 b y=f(x) y x Найти площадь фигуры
- 4. 0 y x y=g (x) y=f (x) b a y = f (x), y = g
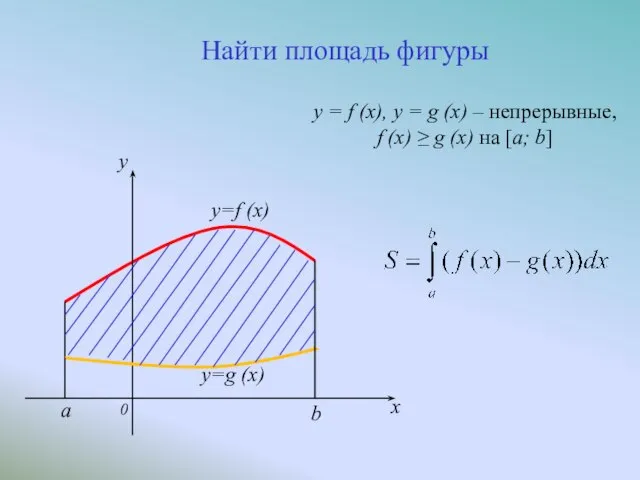
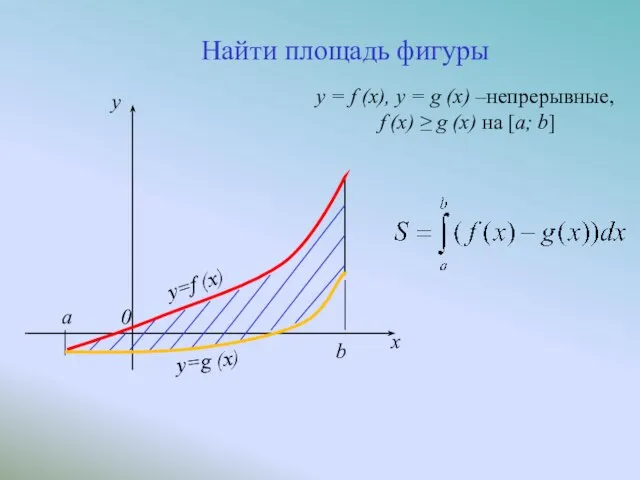
- 5. y=f (x) a y=g (x) b 0 y x Найти площадь фигуры y = f (x),
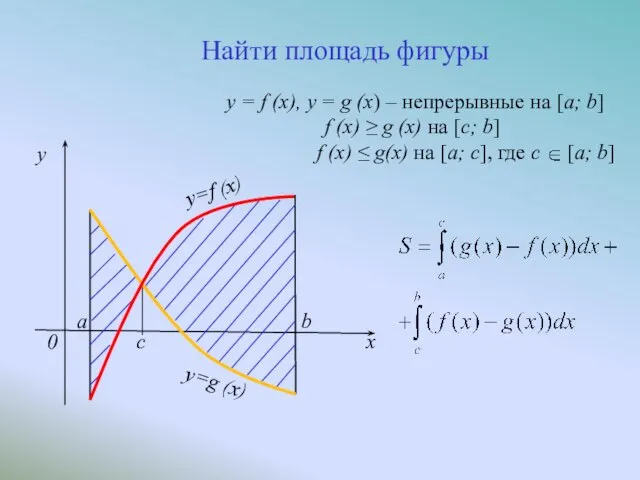
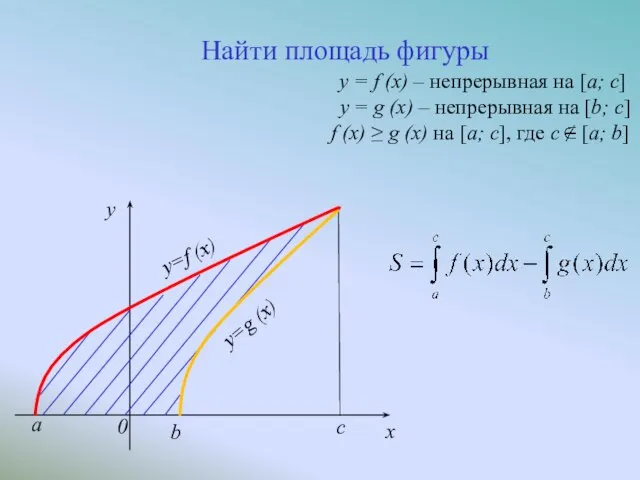
- 6. c x y=f (x) a y=g (x) b 0 y Найти площадь фигуры y = f
- 7. c x y=f (x) a y=g (x) b 0 y Найти площадь фигуры y = f
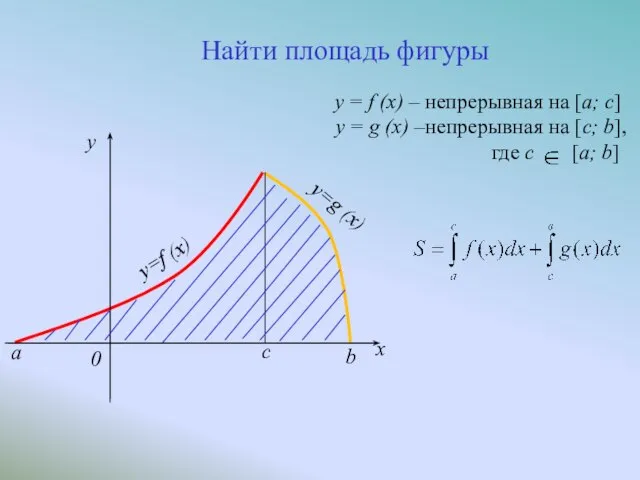
- 8. c x y=f (x) a y=g (x) b 0 y Найти площадь фигуры y = f
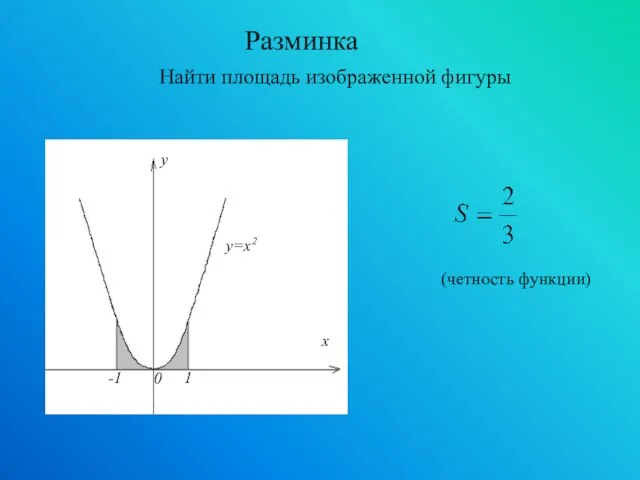
- 9. (четность функции) Разминка Найти площадь изображенной фигуры
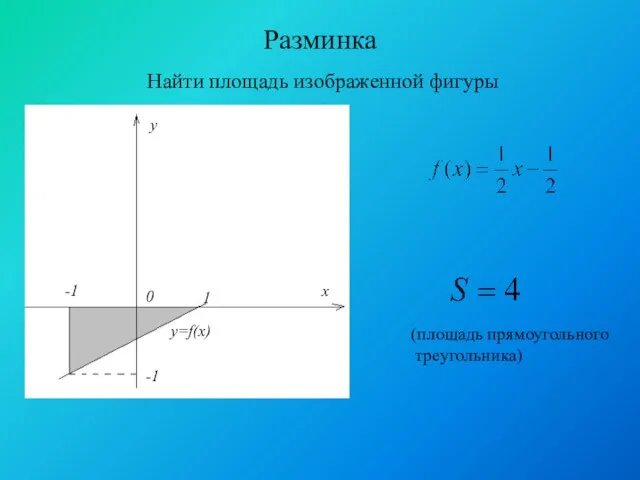
- 10. Разминка Найти площадь изображенной фигуры (площадь прямоугольного треугольника)
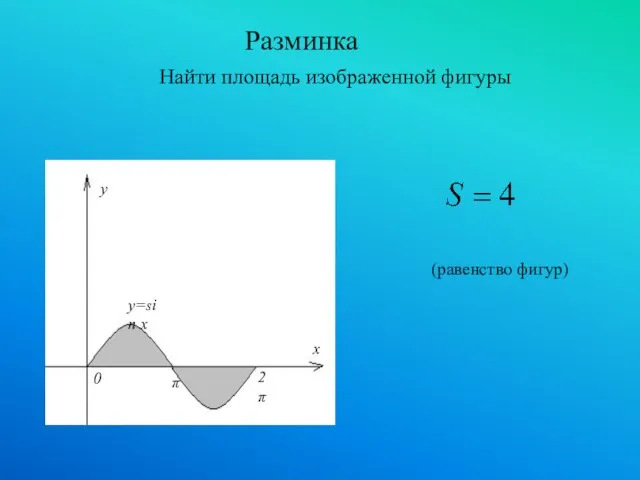
- 11. Разминка Найти площадь изображенной фигуры (равенство фигур)
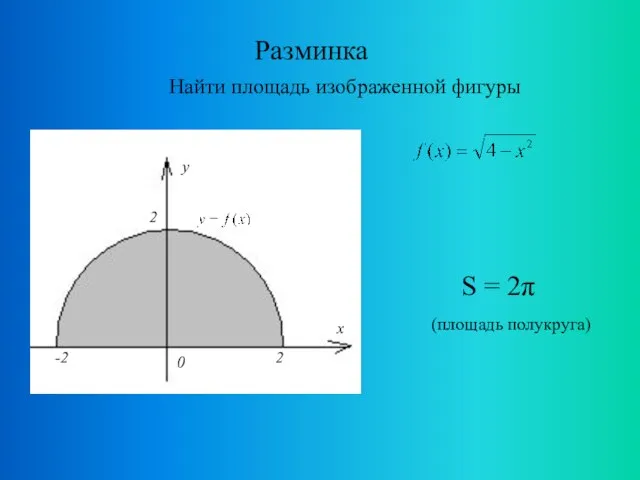
- 12. Разминка Найти площадь изображенной фигуры S = 2π (площадь полукруга)
- 13. Разминка Найти площадь изображенной фигуры S = 1 (площадь треугольника)
- 14. Задачи 1) Найти площадь фигуры, ограниченной линиями
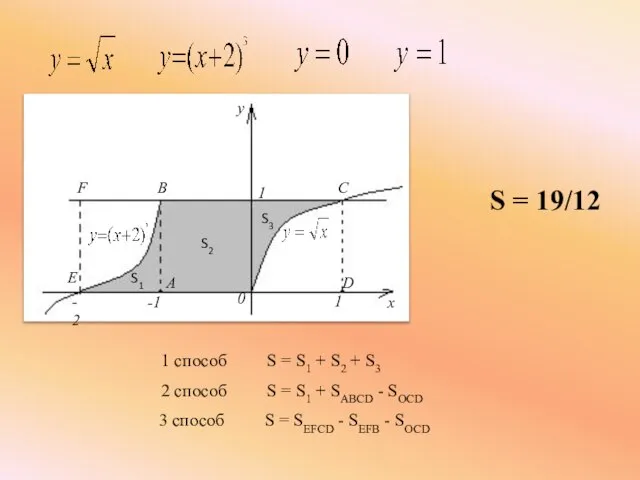
- 15. 1 способ S = S1 + S2 + S3 S = 19/12 2 способ S =
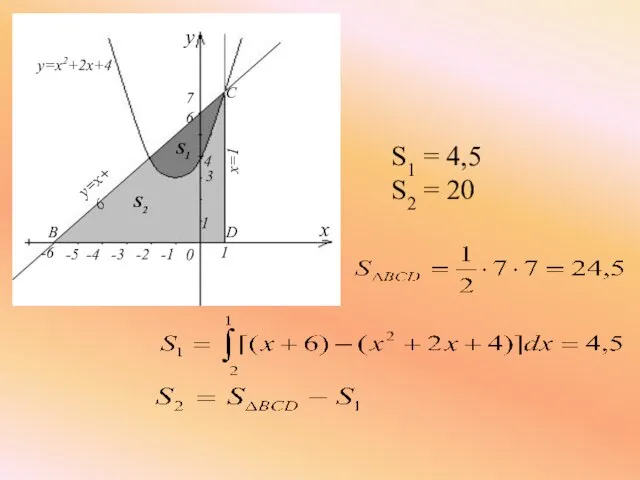
- 16. 2) Фигура, ограниченная линиями y=x+6, x=1, y=0, делится параболой y=x2 + 2x + 4 на две
- 17. S1 = 4,5 S2 = 20 1
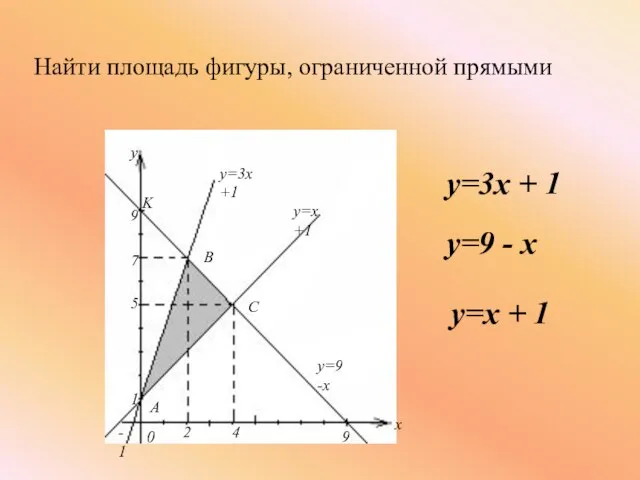
- 18. Найти площадь фигуры, ограниченной прямыми y=3x + 1 y=9 - x y=x + 1
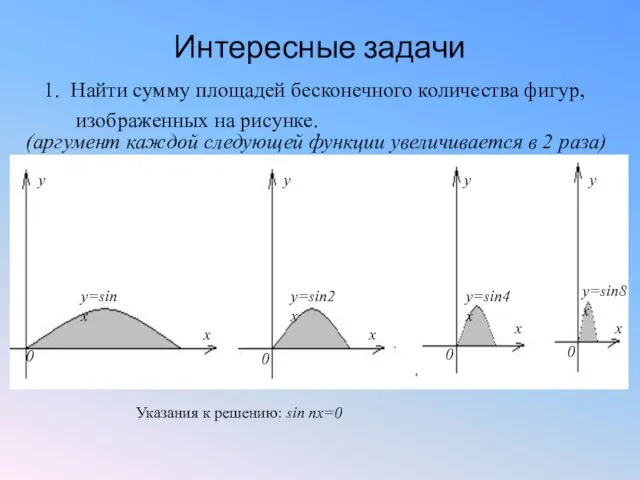
- 19. Интересные задачи 1. Найти сумму площадей бесконечного количества фигур, изображенных на рисунке. (аргумент каждой следующей функции
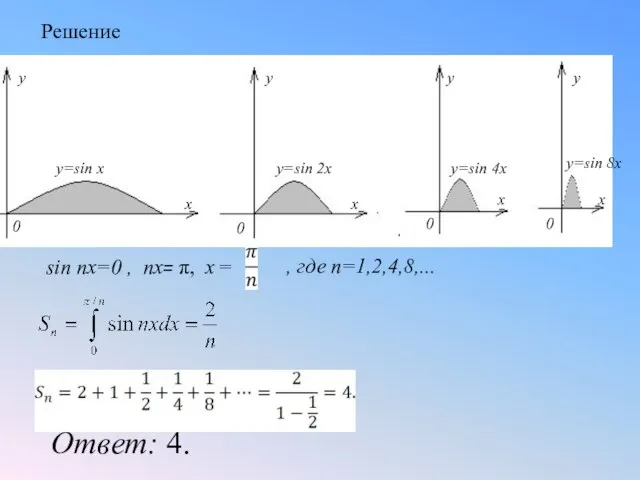
- 20. Ответ: 4. , где n=1,2,4,8,... sin nx=0 , nx= π, x = Решение
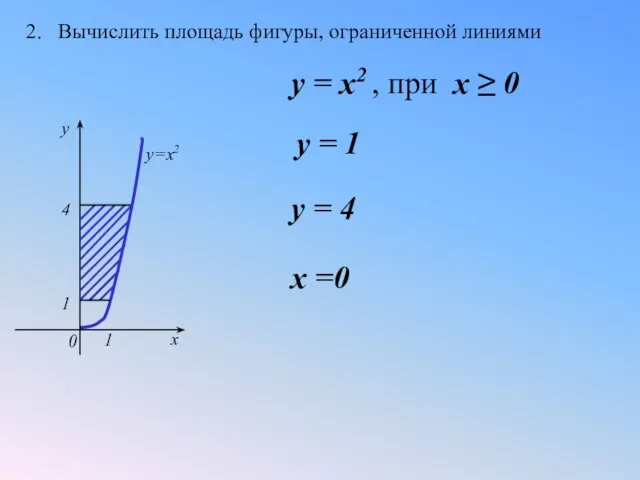
- 21. 2. Вычислить площадь фигуры, ограниченной линиями 1 1 4 0 x y y=x2 y = 1
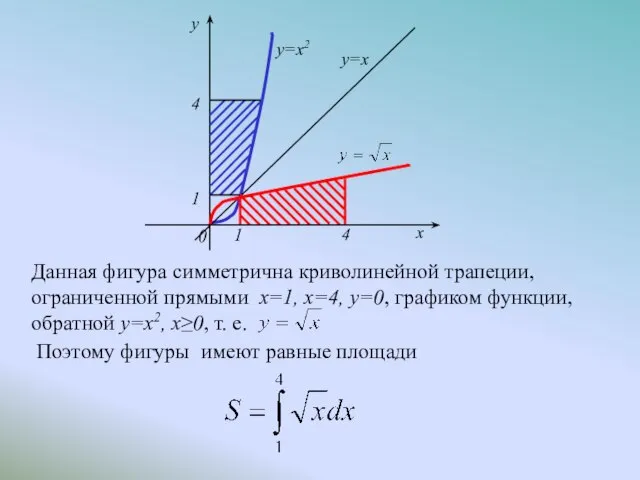
- 22. Данная фигура симметрична криволинейной трапеции, ограниченной прямыми x=1, x=4, y=0, графиком функции, обратной y=x2, x≥0, т.
- 23. Если фигура ограничена линиями x=ϕ1(y), x=ϕ2(y), y=c; y=d, где c то ее площадь может быть вычислена
- 25. Скачать презентацию
![Найти площадь фигуры y=f (x) непрерывная f(x)≥0 на [a; b] a 0 b x y=f(x) y](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/304466/slide-1.jpg)
![y=f(x) непрерывная f(x)≤0 на [a; b] a 0 b y=f(x) y x Найти площадь фигуры](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/304466/slide-2.jpg)




 Презентация на тему Система образования в Германии
Презентация на тему Система образования в Германии  Преобразование графиков функций
Преобразование графиков функций Презентация на тему Протекционизм
Презентация на тему Протекционизм  Презентация на тему Порядок и особенности прохождения государственной службы в таможенных
Презентация на тему Порядок и особенности прохождения государственной службы в таможенных  Svoystva-korney-v-stepeni-n.ppt
Svoystva-korney-v-stepeni-n.ppt Специальные методы решения квадратных уравнений
Специальные методы решения квадратных уравнений Лекции по алгебре и началам анализа 10 класс
Лекции по алгебре и началам анализа 10 класс 10 05.ppt
10 05.ppt РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ  Неравенства с двумя переменными
Неравенства с двумя переменными ЭВМ
ЭВМ Алгебраические кривые в полярной системе координат и их применение в природе и технике
Алгебраические кривые в полярной системе координат и их применение в природе и технике Математический язык. Математическая модель
Математический язык. Математическая модель  ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук
ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук  Алгебраическая дробь. Сокращение дробей
Алгебраическая дробь. Сокращение дробей Презентация на тему ХУДОЖЕСТВЕННАЯ ЛИТЕРАТУРА В ДОУ
Презентация на тему ХУДОЖЕСТВЕННАЯ ЛИТЕРАТУРА В ДОУ  Законы булевой алгебры
Законы булевой алгебры Возрастание и убывание функций
Возрастание и убывание функций Logarifmicheskaya-funkciya.ppt
Logarifmicheskaya-funkciya.ppt Выпуклость и вогнутость функции
Выпуклость и вогнутость функции Одночлены и их особенности
Одночлены и их особенности Решение систем уравнений второй степени с двумя переменными
Решение систем уравнений второй степени с двумя переменными Pervoobraznaya.ppt
Pervoobraznaya.ppt Презентация на тему Понятие национального богатства
Презентация на тему Понятие национального богатства  Арифметическая прогрессия
Арифметическая прогрессия Логические законы и правила преобразования логических выражений
Логические законы и правила преобразования логических выражений Арифметические действия над положительными и отрицательными числами
Арифметические действия над положительными и отрицательными числами Квадратичная функция 9 класс
Квадратичная функция 9 класс